
- •Определители поля. Примеры поля комплексных чисел?
- •Алгебраическая запись комплексного числа. Операции над комплексными числами, их св-ва?
- •Сопряжения и его свойства?
- •4.Модуль и аргумент комплексного числа, их свойства. Тригонометрическая форма записи числа. Формула муравла.
- •Извлечение корня n-степени из комплексного числа?
- •6.Многочлены. Деление многочленов с остатком?
- •7.Теорема Декарта-Безу, схема Горнера. Пример
- •Доказательство
- •8. Рациональные корни многочлена с целыми коэффициентами. Пример. Основная теорема алгебры. Рациональные корни многочленов с целыми коэффициентами
- •Следствие
- •Действительная функция комплексного переменного f(X) непрерывная в замкнутом круге е достигает своего минимума и максимума.
- •Предположим, что это не верно тогда
- •9. Матрицы. Сложение матриц, умножение матриц на число, их свойства.
- •Умножение матрицы на число
- •Свойства умножения матрицы на число
- •10. Умножение матриц, свойства. Пример.
- •11. Транспонирование матриц, свойства. Обратная матрица и её свойства. Транспонирование матриц
- •Транспонирование матрицы
- •Обратная матрица
- •12.Элементарные преобразования строк и столбцов матриц, их матричная интерпретация.
- •18. Алгебраические дополнения элементов матрицы. Разложения определителя по строке.
- •23.Невырожденная матрица. Теорема о существовании обратной матрицы.
- •25. Пространство решений однородной слу. Фундаментальная система решений.
- •27.Структура множества решений слу. Способы решений. Методы решения систем линейных алгебраических уравнений
- •Постановка задачи
- •Правило Крамера
- •Условие совместности системы линейных уравнений
- •28. Пространство геометрических векторов. Операции с векторами и свойства.
- •29. Коллиниарность, комплонарность и линейная зависимость векторов.
- •Линейная зависимость векторов
- •30. Проекция вектора на ось, свойства.
- •31. Скалярное произведение. Критерий ортогональности векторов. Алгебраические свойства скалярного произведения. Скалярное произведение векторов
- •32. Ортонормированный базис. Выражение скалярного произведения через координаты векторов. Длина вектора и угол между ними. Пример.
- •Скалярное произведение векторов в ортонормированном базисе
- •Длина вектора Понятие вектора
- •33. Определение векторного и смешенного произведения векторов. Критерии комплонарности и колинеарности векторов в координатной форме. Площадь паралеограма и объём параллелепипеда.
- •34.Свойство векторного и смешенного произведения. Геометрические свойства векторного произведения Править
- •Алгебраические свойства векторного произведения Править
- •Выражение для векторного произведения в декартовых координатах Править
- •Свойства
- •35.Выражение векторного и смешенного произведения через координаты векторов.
- •8.4. Некоторые приложения смешанного произведения
- •36.Пдск. Координаты точки и координаты векторов. Преобразование координат при переходе к другой пдск.
- •Система координат и координаты вектора
- •37. Пск. Формулы перехода в пдск. Другие системы координат. Полярные координаты
- •[Править]Цилиндрические координаты
- •[Править]Сферические координаты
- •[Править]Обозначения, принятые в Америке
- •[Править]Европейские обозначения
- •38. Понятие об уравнении фигуры. Объединение пересечение фигур.
- •39. Уравнения примой на плоскости.
- •Уравнение прямой по точке и вектору нормали
- •Уравнение прямой, проходящей через две точки
- •Уравнение прямой по точке и угловому коэффициенту
- •Уравнение прямой по точке и направляющему вектору
- •Уравнение прямой в отрезках
- •Нормальное уравнение прямой
- •40. Уравнение плоскости.
- •41. Уравнение прямой в пространстве.
- •42. Угол между прямыми, плоскостями, прямой и плоскостью. Пример. Угол между прямыми на плоскости
- •Угол между плоскостями
- •43. Расстояние от точки до прямой, от точки до плоскости, между прямыми, между плоскостями. Пример. Расстояние от точки до прямой
- •Расстояние от точки до плоскости
- •44. Эллипс. Директрисы и оптические свойства гиперболы. Ллипс
- •46. Парабола. Парабола
- •47. Линейный оператор. Матрица линейного оператора.
- •48. Собственные числа, собственные векторы. Собственные числа и собственные векторы линейного оператора
- •49. Привидение в квп к каноническому виду.
- •50. Поверхности второго порядка. Метод сечений. Поверхности второго порядка
32. Ортонормированный базис. Выражение скалярного произведения через координаты векторов. Длина вектора и угол между ними. Пример.
ртонормированный базис. Если векторы e 1 , e 2 , e 3 попарно перпендикулярны и длина каждого из них равна единице, то базис называетсяортонормированным, а координаты x 1, x 2, x 3 - прямоугольными. Базисные векторы ортонормированного базиса будем обозначать i, j, k.
Будем предполагать, что в пространстве R 3 выбрана правая система декартовых прямоугольных координат {0, i, j, k }.
Скалярное произведение векторов в ортонормированном базисе
Теорема 1.6 (формула вычисления скалярного произведения в ортонормированном базисе). В ортонормированном базисе скалярное произведение векторов равно сумме произведений одноименных координат векторов:
— если
векторы ![]() и
и ![]() относительно
ортонормированного базиса на плоскости
имеют координаты
относительно
ортонормированного базиса на плоскости
имеют координаты ![]() и
и ![]() соответственно,
то скалярное произведение этих векторов
вычисляется по формуле
соответственно,
то скалярное произведение этих векторов
вычисляется по формуле
![]()
— если
векторы
относительно
ортонормированного базиса в пространстве
имеют координаты ![]() и
и ![]() соответственно,
то скалярное произведение этих векторов
вычисляется по формуле
соответственно,
то скалярное произведение этих векторов
вычисляется по формуле
![]()
Докажем
формулу (1.10). Пусть в пространстве задан
ортонормированный (стандартный) базис ![]() .
Скалярные произведения базисных векторов
находятся по определению:
.
Скалярные произведения базисных векторов
находятся по определению:
Используя
линейность скалярного произведения по
любому множителю, для векторов ![]() и
и ![]() получаем:
получаем:
Учитывая (1.11), из девяти слагаемых только три отличны от нуля, поэтому
![]()
что и требовалось доказать.
Замечания 1.10.
1. Для
доказательства формулы (1.9) можно
использовать следующее соображение.
Множество векторов на плоскости со
стандартным базисом ![]() можно
рассматривать как множество таких
векторов в пространстве с базисом
,
у которых аппликата равна нулю. Поэтому
формулу вычисления скалярного произведения
векторов
можно
рассматривать как множество таких
векторов в пространстве с базисом
,
у которых аппликата равна нулю. Поэтому
формулу вычисления скалярного произведения
векторов ![]() и
и ![]() можно
получить из (1.10), полагая
можно
получить из (1.10), полагая ![]() .
.
2. Скалярное
произведение можно записать в матричном
виде: если ![]() и
и ![]() координатные
столбцы векторов
и
в
стандартном базисе, то их скалярное
произведение находится формуле:
координатные
столбцы векторов
и
в
стандартном базисе, то их скалярное
произведение находится формуле:
Для векторов на плоскости соответственно получаем
3. Координаты вектора в ортонормированием базисе равны его скалярным произведениям на соответствующие базисные векторы:
В
самом деле, подставляя в (1.10)
координаты ![]() базисного
вектора
базисного
вектора ![]() ,
приходим к первому равенству (остальные
равенства получаются аналогично).
,
приходим к первому равенству (остальные
равенства получаются аналогично).
4. Формулы (1.9) и (1.10) совместно с геометрическими свойствами скалярного произведения имеют многочисленные приложения (см. разд. 1.6.2).
Пример 1.15. Даны векторы .
Найти скалярные произведения .
Решение. По формуле (1.10) вычисляем
Сравнивая
вектор ![]() со
скалярными произведениями обнаруживаем,
что при умножении вектора на базисный
вектор получается соответствующая
координата данного вектора. Этот
результат иллюстрирует пункт 3 замечаний
1.10.
со
скалярными произведениями обнаруживаем,
что при умножении вектора на базисный
вектор получается соответствующая
координата данного вектора. Этот
результат иллюстрирует пункт 3 замечаний
1.10.
Для
нахождения скалярного произведения
можно использовать матричную запись
(см. пункт 2 замечаний 1.10). Например,
векторам ![]() соответствуют
координатные столбцы
соответствуют
координатные столбцы
Поэтому
что совпадает с полученными ранее результатами.
Пример
1.16. Прямоугольный
параллелепипед ![]() построен
на векторах (см.
рис. 1.38). Точка
построен
на векторах (см.
рис. 1.38). Точка ![]() —
центр грани
—
центр грани ![]() ,
точка
,
точка ![]() делит
ребро
делит
ребро ![]() в
отношении
в
отношении ![]() .
Требуется найти:
.
Требуется найти:
а)
величину ![]() угла
между векторами
угла
между векторами ![]() и
и ![]() ;
;
б)
длину ортогональной проекции вектора
на
прямую ![]() .
.
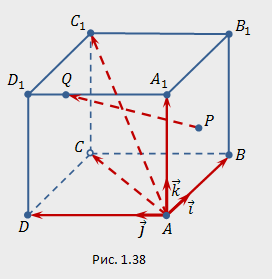
Решение. Находим координаты векторов в стандартном базисе :
(см. решение примера 1.12)
По формуле (1.10) находим скалярные произведения:
а также длины векторов (см. геометрическое свойство 1 скалярного произведения):
Длина ![]() была
найдена в примере 1.12.
была
найдена в примере 1.12.
Теперь по геометрическому свойству 2 находим косинус искомого угла
т.е. ![]()
Алгебраическое значение длины ортогональной проекции находим по геометрическомусвойству 3:
