
- •Определители поля. Примеры поля комплексных чисел?
- •Алгебраическая запись комплексного числа. Операции над комплексными числами, их св-ва?
- •Сопряжения и его свойства?
- •4.Модуль и аргумент комплексного числа, их свойства. Тригонометрическая форма записи числа. Формула муравла.
- •Извлечение корня n-степени из комплексного числа?
- •6.Многочлены. Деление многочленов с остатком?
- •7.Теорема Декарта-Безу, схема Горнера. Пример
- •Доказательство
- •8. Рациональные корни многочлена с целыми коэффициентами. Пример. Основная теорема алгебры. Рациональные корни многочленов с целыми коэффициентами
- •Следствие
- •Действительная функция комплексного переменного f(X) непрерывная в замкнутом круге е достигает своего минимума и максимума.
- •Предположим, что это не верно тогда
- •9. Матрицы. Сложение матриц, умножение матриц на число, их свойства.
- •Умножение матрицы на число
- •Свойства умножения матрицы на число
- •10. Умножение матриц, свойства. Пример.
- •11. Транспонирование матриц, свойства. Обратная матрица и её свойства. Транспонирование матриц
- •Транспонирование матрицы
- •Обратная матрица
- •12.Элементарные преобразования строк и столбцов матриц, их матричная интерпретация.
- •18. Алгебраические дополнения элементов матрицы. Разложения определителя по строке.
- •23.Невырожденная матрица. Теорема о существовании обратной матрицы.
- •25. Пространство решений однородной слу. Фундаментальная система решений.
- •27.Структура множества решений слу. Способы решений. Методы решения систем линейных алгебраических уравнений
- •Постановка задачи
- •Правило Крамера
- •Условие совместности системы линейных уравнений
- •28. Пространство геометрических векторов. Операции с векторами и свойства.
- •29. Коллиниарность, комплонарность и линейная зависимость векторов.
- •Линейная зависимость векторов
- •30. Проекция вектора на ось, свойства.
- •31. Скалярное произведение. Критерий ортогональности векторов. Алгебраические свойства скалярного произведения. Скалярное произведение векторов
- •32. Ортонормированный базис. Выражение скалярного произведения через координаты векторов. Длина вектора и угол между ними. Пример.
- •Скалярное произведение векторов в ортонормированном базисе
- •Длина вектора Понятие вектора
- •33. Определение векторного и смешенного произведения векторов. Критерии комплонарности и колинеарности векторов в координатной форме. Площадь паралеограма и объём параллелепипеда.
- •34.Свойство векторного и смешенного произведения. Геометрические свойства векторного произведения Править
- •Алгебраические свойства векторного произведения Править
- •Выражение для векторного произведения в декартовых координатах Править
- •Свойства
- •35.Выражение векторного и смешенного произведения через координаты векторов.
- •8.4. Некоторые приложения смешанного произведения
- •36.Пдск. Координаты точки и координаты векторов. Преобразование координат при переходе к другой пдск.
- •Система координат и координаты вектора
- •37. Пск. Формулы перехода в пдск. Другие системы координат. Полярные координаты
- •[Править]Цилиндрические координаты
- •[Править]Сферические координаты
- •[Править]Обозначения, принятые в Америке
- •[Править]Европейские обозначения
- •38. Понятие об уравнении фигуры. Объединение пересечение фигур.
- •39. Уравнения примой на плоскости.
- •Уравнение прямой по точке и вектору нормали
- •Уравнение прямой, проходящей через две точки
- •Уравнение прямой по точке и угловому коэффициенту
- •Уравнение прямой по точке и направляющему вектору
- •Уравнение прямой в отрезках
- •Нормальное уравнение прямой
- •40. Уравнение плоскости.
- •41. Уравнение прямой в пространстве.
- •42. Угол между прямыми, плоскостями, прямой и плоскостью. Пример. Угол между прямыми на плоскости
- •Угол между плоскостями
- •43. Расстояние от точки до прямой, от точки до плоскости, между прямыми, между плоскостями. Пример. Расстояние от точки до прямой
- •Расстояние от точки до плоскости
- •44. Эллипс. Директрисы и оптические свойства гиперболы. Ллипс
- •46. Парабола. Парабола
- •47. Линейный оператор. Матрица линейного оператора.
- •48. Собственные числа, собственные векторы. Собственные числа и собственные векторы линейного оператора
- •49. Привидение в квп к каноническому виду.
- •50. Поверхности второго порядка. Метод сечений. Поверхности второго порядка
28. Пространство геометрических векторов. Операции с векторами и свойства.
Направленные отрезки.
Рассмотрим в пространстве две точки А и В. Они определяют отрезок АВ.
Def 1. Отрезок АВ называется направленным, если его концы А и В упорядочены; если при этом первой является точкаА, а второй — точка В, то А — начало отрезка, а В — его конец.
Направленный отрезок обозначается или .
Def 2. Длиной направленного отрезка называется длина отрезка АВ.
|
|
|
|
|
|
На чертеже направленный отрезок снабжен стрелкой на конце.
Def 3. Направленные отрезки и называются сонаправленными, (обозначается ), если они лежат на параллельных прямых и направлены в одну сторону.
Направленные отрезки и называют противоположно направленными (пишут ), если они лежат на параллельных прямых и направлены в разные стороны.
Направленные отрезки и называются противоположными.
Каждую точку А пространства можно рассматривать как направленный отрезок с совпадающим началом и концом. Этот отрезок обозначается и называется нулевым направленным отрезком. Его длина считается равной нулю, а направление не определено.
Def 4. Два направленных отрезка и считаются эквивалентными, если они сонаправлены и имеют равные длины. (Обозначают ).
Эквивалентность является отношением эквивалентности в множестве всех направленных отрезков, т.к. из определения эквивалентности следует:
1о) отрезок эквивалентен сам себе;
2о) если эквивалентен , то эквивалентен ;
3о) если эквивалентен и — эквивалентен , то эквивалентен .
Так как эквивалентность направленных отрезков является отношением эквивалентности, то множество всех направленных отрезков пространства разбивается на непересекающиеся классы — классы эквивалентности. Классы эквивалентности образуют фактор-множество множества всех направленных отрезков пространства.
Def 5. Множество всех эквивалентных направленных отрезков называется вектором (или свободным вектором).
В школе вектор — это параллельный перенос.
Направление эквивалентных направленных отрезков называется направлением вектора, а их длина — длиной вектора.
Таким образом, любой направленный отрезок однозначно определяет вектор, а вектор — это класс эквивалентных направленных отрезков.
Поэтому часто будем писать: «вектор ».
Длина .
Def 6 Вектор a такой, что называется единичным вектором или ортом. Множество нулевых отрезков называется нулевым вектором . Его длина равна нулю, а направление не определено.
Def 7. Два ненулевых вектора, направления которых совпадают или противоположны, называются коллинеарными. Обозначают . Нулевой вектор считается коллинеарным любому вектору.
Очевидно, что прямые, на которых лежат представители классов коллинеарных векторов, параллельны.
Def 8. Три и более векторов называются комплонарными, если они параллельны некоторой плоскости.
Для определенности любую тройку векторов, содержащую нулевой вектор, считают комплонарной.
Пусть даны два вектора a и b. Из произвольной точки O пространства отложим и . Тогда есть направленный отрезок и значит, определяет вектор.
Покажем, что вектор не зависит от выбора точки O. Для этого выберем другую точку . Пусть , . Тогда — параллелограмм; аналогично, — параллелограмм — параллелограмм , т.е. они определяют один и тот же вектор.
Def 9. Вектор называется суммой векторов и . Пишут: .
Способ сложения векторов, изложенный выше, называется правилом треугольника. Можно также использовать правило параллелограмма.
Суммой
векторов ![]() и
и ![]() называется
вектор
называется
вектор ![]()
![]() Для
любых векторов
Для
любых векторов ![]() справедливы
равенства
справедливы
равенства
|
|
Т![]() еорема 11.6.
еорема 11.6.
Каковы
бы ни были три точки A, B и C,
имеет место векторное равенство ![]()
Пусть A (x1; y1), B (x2; y2), C (x3; y3) – данные точки.
Вектор ![]() имеет
координаты
имеет
координаты ![]() вектор
вектор ![]() имеет
координаты
имеет
координаты ![]() Следовательно,
вектор
Следовательно,
вектор ![]() имеет
координаты
имеет
координаты ![]() Вектор
Вектор ![]() имеет
такие же координаты. По теореме
11.5
Теорема
доказана.
имеет
такие же координаты. По теореме
11.5
Теорема
доказана.
амечание.
Теорема 11.6 дает следующий способ
построения суммы произвольных
векторов |
Правило параллелограмма: для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах.
Разностью
векторов
и
называется
такой вектор ![]() который
в сумме с вектором
который
в сумме с вектором ![]() дает
вектор
дает
вектор ![]()
![]() откуда c1 = a1– b1; c2 = a2– b2.
откуда c1 = a1– b1; c2 = a2– b2.
Произведением
вектора
на
число λ называется
вектор ![]() т. е.
т. е. 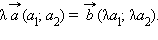
Для любого вектора и чисел λ и μ
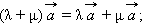
Для любых двух векторов и и числа λ
|
Т еорема 11.7.
Абсолютная
величина вектора ![]() равна |λ || a|.
Направление вектора
при
равна |λ || a|.
Направление вектора
при ![]() совпадает
с направлением вектора
если λ > 0,
и противоположно направлению
вектора
если λ < 0.
совпадает
с направлением вектора
если λ > 0,
и противоположно направлению
вектора
если λ < 0.
Построим
векторы ![]() и
и ![]() равные
и
соответственно
(O –
начало координат). Пусть
равные
и
соответственно
(O –
начало координат). Пусть ![]() и
и ![]() –
координаты вектора
–
координаты вектора ![]() Тогда
координатами точки A будут
числа
и
Тогда
координатами точки A будут
числа
и ![]() координатами
точки B –
числа
координатами
точки B –
числа ![]() и
и ![]() Уравнение
прямой OA имеет
вид: αx + βy = 0.
Так как уравнению удовлетворяют
координаты точкиA (a1; a2),
то ему удовлетворяют и координаты
точки B (λa1; λa2).
Отсюда следует, что точка B лежит
на прямой OA.
Координаты c1 и c2 любой
точки C,
лежащей на луче OA,
имеют те же знаки, что и
координаты a1 и a2 точки A,
и координаты любой точки, которая лежит
на луче, дополнительном к OA,
имеют противоположные знаки.
Уравнение
прямой OA имеет
вид: αx + βy = 0.
Так как уравнению удовлетворяют
координаты точкиA (a1; a2),
то ему удовлетворяют и координаты
точки B (λa1; λa2).
Отсюда следует, что точка B лежит
на прямой OA.
Координаты c1 и c2 любой
точки C,
лежащей на луче OA,
имеют те же знаки, что и
координаты a1 и a2 точки A,
и координаты любой точки, которая лежит
на луче, дополнительном к OA,
имеют противоположные знаки.
Поэтому, если λ > 0, то точка B лежит на луче OA, а следовательно, векторы и одинаково направлены. Если λ < 0, то точка B лежит на дополнительном луче и векторы и противоположно направлены.
Абсолютная
величина вектора
равна ![]() Теорема
доказана.
Теорема
доказана.
Теорема 11.8.
Для
любых отличных от нуля коллинеарных
векторов
и
существует
такое число λ,
что ![]()
Доказательство
Пусть
и
одинаково
направлены. Векторы
и |
Т еорема 11.9.
Пусть
и
–
отличные от нуля неколлинеарные векторы.
Любой вектор ![]() можно
единственным образом представить в
виде
можно
единственным образом представить в
виде ![]()
Доказательство
Пусть A и B –
начало и конец вектора
Для
доказательства единственности
представления допустим, что в условиях
теоремы такое представление не
единственно. То есть наряду с числами
λ и μ такими, что |
Скалярное произведение векторов.
Скалярным
произведением векторов
и
называется
число ![]() Скалярное
произведение векторов
и
обозначется
Скалярное
произведение векторов
и
обозначется ![]()
Для
любых векторов
и ![]() верно:
верно:
Т еорема 11.10.
Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.
Доказательство
Пусть и – данные векторы и φ – угол между ними. Имеем:
или
Скалярное
произведение
|
Единичные
векторы ![]() и
и ![]() имеющие
направления положительных координатных
полуосей, называются координатными
векторами или ортами.
имеющие
направления положительных координатных
полуосей, называются координатными
векторами или ортами.
Т еорема 11.11.
Любой
ненулевой вектор
единственным
образом можно разложить по координатным
векторам, то есть записать в виде ![]()
Доказательство
Так
как координатные векторы отличны от
нуля и неколлинеарны, то любой
вектор
допускает
разложение по этим векторам в силу
теоремы 11.9 |

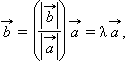
 Если
векторы
и
противоположно
направлены, аналогично заключаем,
что
Если
векторы
и
противоположно
направлены, аналогично заключаем,
что 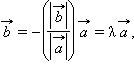
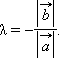 Теорема
доказана.
Теорема
доказана.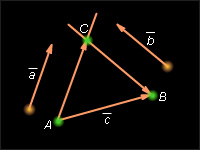
 На
основании теоремы 11.7 и замечания 11.1
получаем, что векторы
и
коллинеарны.
Но это противоречит условию
неколлинеарности этих векторов.
Показанное противоречие доказывает
единственность представления. Теорема
доказана.
На
основании теоремы 11.7 и замечания 11.1
получаем, что векторы
и
коллинеарны.
Но это противоречит условию
неколлинеарности этих векторов.
Показанное противоречие доказывает
единственность представления. Теорема
доказана.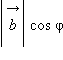 и
и 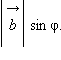 По
определению
По
определению 