27.Структура множества решений слу. Способы решений. Методы решения систем линейных алгебраических уравнений
Прямые методы решения СЛАУ: Метод Крамера Метод обратной матрицы Метод Гаусса
Постановка задачи
Требуется найти решение системы m линейных уравнений, которая записывается в общем виде как
,
Эту систему уравнений можно записать также в матричном виде:
,
где 
, 
, 
.
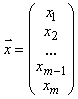A
– матрица системы, 
–
вектор правых частей, 
–
вектор неизвестных.
При
известных A и
требуется
найти такие 
,
при подстановке которых в систему
уравнений она превращается в тождество.
Необходимым и достаточным условием существования единственного решения СЛАУ является условие det A≠0, т.е. определитель матрицы A не равен нулю. В случае равенства нулю определителя матрица A называется вырожденной и при этом СЛАУ либо не имеет решения, либо имеет их бесчисленное множество.
В дальнейшем будем предполагать наличие единственного решения.
Все методы решения линейных алгебраических задач можно разбить на два класса: прямые (точные) и итерационные (приближенные).
Системой 
линейных
алгебраических уравнений
с 
неизвестными называется
система уравнений вида
(5.1)
Числа 
называются коэффициентами
системы; 
— свободными
членами, 
— неизвестными.
Количество
уравнений
в системе может быть меньше, больше или
равно числу
неизвестных.
Решением
системы называется
упорядоченная совокупность
чисел 
такая,
что после замены неизвестных
соответственно
числами 
каждое
уравнение системы превращается в верное
числовое равенство. Система
называется совместной,
если она имеет хотя бы одно решение.
Если система не имеет ни одного решения,
то она называется несовместной.
Система (5.1) называется однородной, если все свободные члены равны нулю:
(5.2)
В отличие от однородной, систему общего вида (5.1) называют неоднородной.
Систему (5.1) принято записывать в матричной форме. Для этого из коэффициентов системы составляем матрицу системы
свободные члены записываем в столбец свободных членов
а неизвестные — в столбец неизвестных
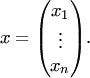
Матричная запись неоднородной системы уравнений (5.1) имеет вид
(5.3)
а однородной:
(5.4)
где
символ 
в
правой части обозначает нулевой столбец
размеров 
.
Матричную запись (5.3) системы уравнений можно представить в эквивалентной форме
Тогда
решение системы представляется
столбцом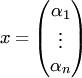 
и
удовлетворяет равенству
(5.5)
т.е. столбец свободных членов является линейной комбинацией столбцов матрицы системы.
Относительно системы уравнений нас интересуют ответы на следующие вопросы:
1. Совместна система или нет?
2. Если система совместна, то имеет ли она единственное решение или нет?
3. Если решение единственное, то как его найти?
4. Если система имеет бесконечно много решений, то какова структура множества решений?
5. Как в бесконечном множестве решений системы определить одно решение, наилучшее с практической точки зрения?
6. Если система несовместна, то как определить ее приближенное решение?
