
- •3. Статистические методы оценки параметров сигналов.
- •3.1 Понятие об оценке параметров принимаемых сигналов.
- •3.2 Качество оценок и критерии оптимальности измерения параметров.
- •3.3 Основные положения байесовской теории измерений
- •3.4 Максимально правдоподобная оценка
- •3.5 Потенциальная точность определения параметра
- •3.6 Потенциальная точность определения момента прихода сигнала
- •3.7 Потенциальная точность определения доплеровского сдвига частоты.
- •4. Пространственно временная обработка сигналов.
- •4.1 Пространственно-временной сигнал.
- •4.2 Случайные пространственно-временные сигнала
- •4.3 Случайные поля и пространственные фильтры
- •4.4 Линейная фильтрация стационарных пространственно-временных сигналов
- •5. Основы цифровой обработки сигналов.
- •5.1 Модели дискретных сигналов
- •5.2 Дискретизация периодических сигналов
- •5.3 Основы теории z-преобразования
- •5.4 Цифровые фильтры
- •5.5 Трансверсальные цифровые фильтры
- •5.6 Рекурсивные цифровые фильтры
- •5.7 Основы гомоморфной обработки сигналов
- •5.8 Гомоморфная обработка мультипликативного сигнала
- •5.9 Гомоморфная обработка свернутого сигнала
- •5.9 Кепстральный анализ сигналов
5.9 Кепстральный анализ сигналов
Исторически понятие “кепстр” было определено временем:
![]() (5.53)
(5.53)
где Φs(jω) – амплитудный спектр непрерывного сигнала.
Поскольку │Φs(jω)│2 имеет смысл спектральной плотности энергии сигнала s(t), то Сs(q) истолковывается как энергетический спектр функции ln│Φs(jω)│2.
Но из (5.53) очевидно, что аргумент q этого “спектра” [в кавычках] имеет размерность времени, а не частоты. Этим и объясняется распространение термина “кепстр”, который образован перестановкой букв в термине “спектр”. (В зарубежной литературе аргумент называется “quefrecy”, сто по-русски выглядит как “сачтота”).
Хотя q имеет размерность времени, это особое, кепстральное время, поскольку Сs(q) в любой момент q зависит от функции s(t), заданной при -∞<t<∞.
Определяемый выражением (5.53) кепстр принято называть кепстром мощности. Фазо-частотная характеристика спектра сигнала Φs(jω) в кепстре мощности не учитывается.
Кепстры мощности получили распространение при анализе сигналов, представляющих собой свертку двух функций времени, таких, что после преобразования s(t) по алгоритму (5.53) образуются непрерывающиеся на оси q импульсы.
Следует отметить, что выражение (5.53)
имеет смысл не для любого сигнала –
s(t).
Действительно, для сигнала с конечной
энергией выполняется
![]() ,
из которого следует, что при │ω│→∞
│Φ(jω)│2→0. Но тогда
при │ω│→∞ обращается в бесконечность
│ln│Φ(jω)││
и интеграл
,
из которого следует, что при │ω│→∞
│Φ(jω)│2→0. Но тогда
при │ω│→∞ обращается в бесконечность
│ln│Φ(jω)││
и интеграл![]() расходится. Это противоречие устраняется,
если спектр сигнала ограничен верхней
частотой ±ωв, и тогда значение
функции
ограничено.
расходится. Это противоречие устраняется,
если спектр сигнала ограничен верхней
частотой ±ωв, и тогда значение
функции
ограничено.
Рассмотрим пример применения кепстра мощности. Пусть задан сигнал s(t) на выходе линейного тракта и требуется получить информацию об исходном сигнале s1(t), действующем на его входе, а также об импульсной характеристике g(t) самого тракта. Связь между тремя перечисленными функциями времени определяется сверткой:
s(t)=s1(t)*g(t)
Подобная задача возникает при анализе сейсмических процессов, при использовании локационных методов определения характеристик среды распространения при анализе сигналов речи и т.д.
В частности, при разработке электронных синтезаторов речи под s1(t) подразумевается сигнал, о котором известно только, сто его спектральная плотность S1(ω) заключается в некоторой полосе │ω│≤ωмах, а форма спектра характеризуется периодической изрезанностью, однако период пульсации 1/Т (по оси частот), а также амплитуда пульсации подлежат определению. Об импульсной характеристике речевого тракта g(t) только известно, что ее продолжительность мала по сравнению с Т, так что передаточная функция тракта K(jω) изменяется плавно по сравнению с пульсацией Φ1(jω).
Результаты обработки сигнала s(t)=s1(t)*g(t) в схеме:
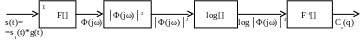
После Фурье-преобразования, определения квадрата модуля спектра, а также логарифмирования получается функция:
log│Φ(jω)│2= log│Φ1(jω)│2+ log│К(jω)│2.
Эта функция подвергается обратному преобразованию Фурье (5.53), в результате которого получается 2 слагаемых кепстра мощности:
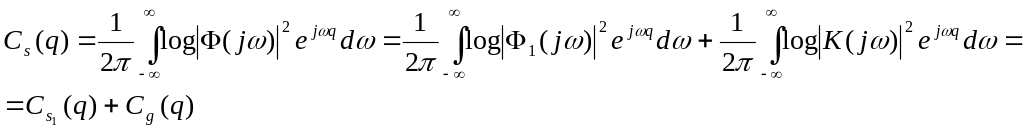
Вид соответствующих функций показан на рисунке:
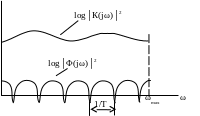
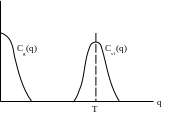
Функции log│Φ1(jω)│2, изменяющейся с периодом 1/Т, соответствует кепстр Сs1(q) в виде пика при q=T, медленному же изменению функции log│К(jω)│2 соответствует кепстр Сg(q), расположенный вблизи q=0 (область малого кепстрального времени).
Таким образом можно выявить основную частоту 1/Т, а также получить некоторую информацию о форме АЧХ тракта.
В отличие от рассмотренной упрощенной модели со строго периодической пульсацией спектра Φ1(jω) и с постоянной во времени передаточной функцией К(jω) при обработке реальных речевых сигналов приходиться иметь дело с “квазипериодическим” процессом, частота которого меняется во времени. То же относится к функции К(jω). Путем усреднения по большому числу отрезков реализаций, в пределах которых функции Φ1(jω) и К(jω) практически неизменны, удается выявить средние частоты и параметры тракта, необходимые для синтезов звука речи.
На практике Кепстральный анализ, как правило, проводится в цифровой форме. Его применяют, в частности, для определения времени задержки сигнала при эхолокации, выявления формы приходящих сигналов.
