4. Геометрический смысл и физический смысл линейных операций с векторами: сумма векторов , и умножение вектора на вещественное число .

а)Суммой двух векторов называется вектор, имеющий начало в начале вектора , а конец – в конце вектора , при условии, что вектор приложен к концу вектора .

В соответствии с определением слагаемые и их сумма 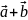образуют треугольник (рис.ниже). Поэтому данное правило сложения двух векторов называют «правилом треугольника».

О перация сложения векторов обладает свойствами:

1. (коммутативность);

2. , (ассоциативность);

3. для любого вектора (особая роль нулевого вектора);

4. Для каждого вектора существует противоположный ему вектор такой, что (для получения достаточно поменять местами начало и конец вектора ).

Вектор противоположный вектору обозначают

б) Произведением вектора на вещественное число λ (скаляр) называется вектор , такой, что 1) ; 2) вектор коллинеарен вектору ; 3) векторы и имеют одинаковое (противоположное) направление если λ > 0 (λ < 0).

Замечание: В случае, когда λ = 0 или произведение является нулевым вектором.

7.Определение линейной зависимости совокупности векторов , ,…, : привести два определения и показать их равносильность.

Пусть задана система векторов а₁, а₂, а₃,…,а_n (1) одной размерности.

Определение: система векторов (1) называется линейно-независимой, если равенство a₁ а₁+a₂ а₂+…+ a_n а_n =0 (2) выполняется лишь в том случае, когда все числа a₁, a₂,…, a_n=0 и Î R

Определение: система векторов (1) называется линейно-зависимой, если равенство (2) выполнимо хотя бы при одном a _{i ¹} 0 (i=1,…,k)

Свойства

Если система векторов содержит нулевой вектор, то она линейно зависима

Если система векторов содержит линейно-зависимую подсистему векторов, то она будет линейно-зависимой.

Если система векторов линейно-независима, то и любая ее подсистема будет линейно независимой.

Если система векторов содержит хотя бы один вектор, являющийся линейной комбинацией других векторов, то эта система векторов будет линейно зависимой.

8.Определение базиса для векторов, расположенных на плоскости и в пространстве. Что значит – базис ортогональный?

Базис — множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества - базисных векторов.

Базисом на плоскости называются два неколлинеарных вектора на этой плоскости, взятые в определённом порядке. Эти векторы называются базисными.

Базисом в пространстве называются три некомпланарных вектора , взятые в определённом порядке. Эти векторы называются базисными.

Ортогональный базис — базис, составленный из попарно ортогональных векторов. (пример: декартова система координат).

9.Определение, физический смысл и основные свойства скалярного произведения векторов , . Вычисление скалярного произведения.

а)Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними. Данной операции соответствует умножение длины данного вектора на проекцию другого вектора на данный вектор .

Свойства скалярного произведения:

1. коммутативность: ( , )=( , )

2. ( , )=| |²

3. ( , )=0 <=>

4. Дистрибутивность: ( ₁+ ₂, )= ( ₁, )+ ₂, )

5. ( , λ· )= λ·( , ) λ R.

б) Вычисление скалярного произведения:

1) ={x₁,y₁,z₁}, ={x₂,y₂,z₂}, то ( , )=x₁·x₂+y₁·y₂+z₁·z₂

2) ( , )=| |·| |·cosφ

10. Заданы векторы = и = . Как вычислить проекцию вектора на направление, определяемое вектором ?

= , = , то ( , )=

11. Заданы векторы = и = . Как вычислить угол между векторами и ?

Угол между двумя ненулевыми векторами определяется с помощью вычисления скалярного произведения. По определению скалярное произведение равно произведению длин векторов на косинус угла между ними. С другой стороны, скалярное произведение для двух векторов с координатами (x₁; y₁) и с координатами (x₂; y₂) вычисляется по формуле: ab = x₁x₂ + y₁y₂. Из этих двух способов нахождения скалярного произведения легко найти угол между векторами.

Найти длины или модули векторов. Для наших векторов и : | | = (x₁² + y₁²)^1/2, | | = (x₂² + y₂²)^1/2. из

Найти скалярное произведение векторов, перемножив их координаты попарно: ( b) = x₁x₂ + y₁y₂. Из определения скалярного произведения ( ) = | |*| |*cos α, где α - угол между векторами. Тогда получим, что x₁x₂ + y₁y₂ = | |*| |*cos α. Тогда cos α = (x₁x₂ + y₁y₂)/(| |*| |) = (x₁x₂ + y₁y₂)/((x₁² + y₁²)(x₂² + y₂²))^1/2.

Если заданы координаты вектора в пространстве, то просто добавляем координату z_i

1. Определители второго порядка как следствие решения системы уравнений именно, получение выражений: и , где = = , = = = и = = - определители 2-го порядка. Свойства определителя второго порядка.

Пусть дана квадратная таблица из четырех чисел , , , :

(1)

Число называется определителем второго порядка, соответствующего таблице (1). Этот определитель обозначается символом ; соотвественно имеем

(2).

Рассмотрим систему двух уравнений

(3)

с двумя неизвестными x, y. (Коэффициенты , , , и свободные члены , предположим данными.) Введем обозначения

, , (4)

Определитель , составленный из коэффициентов при неизвестных системы (3), называется определителем этой системы. Определитель получается путем замены элементов первого столбца определителя свобдными членами системы (3); определитель при помощи замены свободными членами системы (3) элементов его второго столбца.

Если , то система (3) имеет единственное решение; оно определяется формулами

, .

Если и при этом хотя бы один из определителей , отличен от нуля, то система (3) совсем не имеет решений (как говорят, уравнения этой системы несовместны).

Если же , но также , то система (3) имеет бесконечно много решений (в этом случае одно из уравнений системы есть следствие другого).

2. Геометрический смысл решения системы двух уравнений с двумя неизвестными. Что значит каждая из ситуаций: а) ; б) =0 и = =0; в) =0 и хотя бы одно из чисел , 0.

Пусть на плоскости задана аффинная система координат . Как показано ниже, множество точек , координаты которых удовлетворяют линейному уравнению с двумя неизвестными , или , представляет собой прямую. Поэтому множество решений системы уравнений является пересечением прямых .