
34.Неравенство Чебышева
Если Х-случайная величина, математическое ожидание которой М(Х)=а, а дисперсия D(Х) конечна, то для любого числа E>0 выполняются неравенства:
 -
первое неравенство Чебышева
-
первое неравенство Чебышева
 -
второе неравенство Чебышева
-
второе неравенство Чебышева
Правило «трех сигм».
Найдем вероятность того, что нормально распределенная случайная величина примет значение из интервала (а - 3σ, а + 3σ):
Следовательно, вероятность того, что значение случайной величины окажется вне этого интервала, равна 0,0027, то есть составляет 0,27% и может считаться пренебрежимо малой. Таким образом, на практике можно считать, что все возможные значения нормально распределенной случайной величины лежат в интервале (а - 3σ, а + 3σ).
Полученный результат позволяет сформулировать правило «трех сигм»: если случайная величина распределена нормально, то модуль ее отклонения от х = а не превосходит 3σ.
33.
Неравенство Маркова. Обобщенное
неравенство Чебышева.
Если для случайной величины X
существует
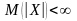 ,
то для любого
,
то для любого
 справедливо неравенство
Маркова
справедливо неравенство
Маркова
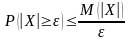 .
.
Оно
вытекает из обобщенного
неравенства Чебышева:
Пусть функция
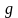 монотонно возрастает и неотрицательна
на
монотонно возрастает и неотрицательна
на
 .
Если для случайной величины X
существует
.
Если для случайной величины X
существует
 ,
то для любого
справедливо неравенство
,
то для любого
справедливо неравенство
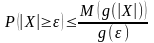 .
.
13.
Операции над случайными величинами.
Сумма, разность и произведение случайных
величин. Примеры.
Две дискретные случайные величины X
и Y,
заданные законами распределения
соответственно
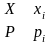 и
и
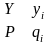 ,
называются независимыми,
если события
,
называются независимыми,
если события
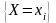 и
и
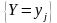 независимы для всех значений
независимы для всех значений
 и
и
 .
Это означает, что
.
Это означает, что
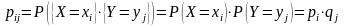 .
.
Суммой
(разностью) случайных величин
X
и Y
называется случайная величина
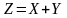
 ,
принимающая все значения вида
,
принимающая все значения вида
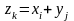
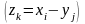 .
При этом P(Z
=
zk)
=
.
При этом P(Z
=
zk)
=

 .
Произведением
случайных величин
X
и Y
называется случайная величина
.
Произведением
случайных величин
X
и Y
называется случайная величина
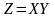 ,
принимающая все значения вида
,
принимающая все значения вида
 .
При этом P(Z
=
zk)
=
.
При этом P(Z
=
zk)
=
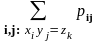 .
.
14.
Математическое ожидание дискретной
случайной величины и его свойства.
Математическое
ожидание
дискретной случайной величины
– это сумма парных произведений всех
возможных ее значений на соответствующие
вероятности:
![]() ,
где
.
,
где
.
Очевидно,
математическое ожидание случайной
величины
не изменится, если таблицу значений
этой случайной величины пополнить
конечным числом любых чисел, считая,
что вероятности этих чисел равны нулю.
Математическое ожидание
![]() случайной величины есть величина
постоянная и поэтому представляет
числовую характеристику случайной
величины
.
случайной величины есть величина
постоянная и поэтому представляет
числовую характеристику случайной
величины
.
Свойства математического ожидания: 1) Теорема. Математическое ожидание постоянной величины равно этой величине. 2) Теорема. Математическое ожидание суммы двух (или нескольких) случайных величин и равно разности их математических ожиданий:
![]() .Следствие.
Если
– постоянная величина, то:
.Следствие.
Если
– постоянная величина, то:
![]() 3) Теорема. Математическое ожидание
произведения двух независимых случайных
величин
и
равно произведению их математических
ожиданий:
3) Теорема. Математическое ожидание
произведения двух независимых случайных
величин
и
равно произведению их математических
ожиданий:![]() .
Следствие.
Математическое ожидание произведения
нескольких взаимно независимых случайных
величин равно произведению математических
ожиданий этих величин. Действительно,
например, для трех взаимно независимых
случайных величин
,
и
.
Следствие.
Математическое ожидание произведения
нескольких взаимно независимых случайных
величин равно произведению математических
ожиданий этих величин. Действительно,
например, для трех взаимно независимых
случайных величин
,
и
![]() :
:
![]() ,
и т.д.
,
и т.д.
Следствие.
Постоянный множитель можно выносить
за знак математического ожидания,
т.е.![]() .
.
Если – постоянная величина и – любая случайная величина, то, учитывая, что и – независимы, получим:
![]() .
.
Следствие. Математическое ожидание разности двух случайных величин и равно разности их математических ожиданий: .
35.
Закон больших чисел в форме Чебышева.
Его смысл. Следствие закона больших
чисел в форме Чебышева. Закон больших
чисел в форме Бернулли.
Под законом
больших чисел
в теории вероятностей понимается ряд
теорем, в каждой из которых устанавливается
факт асимптотического приближения
среднего значения большого числа
опытных данных к математическому
ожиданию случайной величины. В основе
доказательств этих теорем лежит
неравенство Чебышева. Это неравенство
можно получить, рассматривая дискретную
случайную величину, имеющую
возможных значений
![]() .
.
Теорема.
Пусть
имеется конечная последовательность
![]() независимых случайных величин, с одним
и тем же математическим ожиданием
и дисперсиями, ограниченными одной и
той же постоянной
:
независимых случайных величин, с одним
и тем же математическим ожиданием
и дисперсиями, ограниченными одной и
той же постоянной
:
![]()
![]() .
.
Тогда,
каково бы ни было число
![]() ,
вероятность события
,
вероятность события
![]()
стремится к единице при .
Теорема Чебышева устанавливает связь между теорией вероятностей, которая рассматривает средние характеристики всего множества значений случайной величины, и математической статистикой, оперирующей ограниченным множеством значений этой величины. Она показывает, что при достаточно большом числе измерений некоторой случайной величины среднее арифметическое значений этих измерений приближается к математическому ожиданию.
36.
Центральная предельная теорема и ее
смысл.
Пусть случайные величины
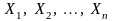 независимы и одинаково распределены
со средними
независимы и одинаково распределены
со средними
 и дисперсиями
и дисперсиями
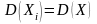 .
Пусть, кроме того,
.
Пусть, кроме того,
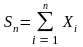 и
и
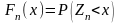 – функция распределения случайной
величины
– функция распределения случайной
величины
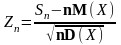 .
Тогда
.
Тогда
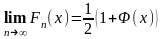 ,
то есть закон распределения случайной
величины
,
то есть закон распределения случайной
величины
 при
при
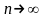 стремится к стандартному нормальному
закону (здесь
стремится к стандартному нормальному
закону (здесь
 – функция Лапласа). Заметим, что
– функция Лапласа). Заметим, что
 .
.
39. Построение интервального вариационного ряда. Формула Стерджесса. Гистограмма и полигон частот и относительных частот. Полигоном частот
называют
ломаную линию, отрезки которой соединяют
точки
![]() .
Для построения полигона частот на оси
абсцисс откладывают варианты
,
а на оси ординат – соответствующие им
частоты
.
Для построения полигона частот на оси
абсцисс откладывают варианты
,
а на оси ординат – соответствующие им
частоты
![]() и соединяют точки
и соединяют точки
![]() отрезками
прямых.
отрезками
прямых.
Полигон
относительных частот
строится
аналогично, за исключением того, что
на оси ординат откладываются относительные
частоты
![]() .
.
В случае непрерывного признака строится гистограмма, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала – сумму частот вариант, попавших в i–й интервал.
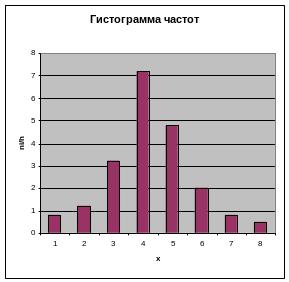
Гистограммой
частот
называют
ступенчатую фигуру, состоящую из
прямоугольников, основаниями которой
служат частичные интервалы длиною h,
а высоты равны отношению
![]() .
Для построения гистограммы частот на
оси абсцисс откладывают частичные
интервалы, а над ними проводят отрезки,
параллельные оси абсцисс на расстоянии
(высоте)
.
Площадь i–го
прямоугольника равна
.
Для построения гистограммы частот на
оси абсцисс откладывают частичные
интервалы, а над ними проводят отрезки,
параллельные оси абсцисс на расстоянии
(высоте)
.
Площадь i–го
прямоугольника равна
![]() – сумме частот вариант i–о
интервала, поэтому площадь гистограммы
частот равна сумме всех частот, т.е.
объему выборки.
– сумме частот вариант i–о
интервала, поэтому площадь гистограммы
частот равна сумме всех частот, т.е.
объему выборки.
В
случае гистограммы относительных
частот по оси ординат откладываются
относительные частоты
,
на оси абсцисс – частичные интервалы,
над ними проводят отрезки, параллельные
оси абсцисс на высоте
![]() .
Площадь i–го
прямоугольника равна относительной
частоте вариант
.
Площадь i–го
прямоугольника равна относительной
частоте вариант
![]() ,
попавших в i–й
интервал. Поэтому площадь гистограммы
относительных частот равна сумме всех
относительных частот, то есть единице.
,
попавших в i–й
интервал. Поэтому площадь гистограммы
относительных частот равна сумме всех
относительных частот, то есть единице.

40.
Числовые характеристики выборки
(Выборочные средняя дисперсия,
исправленная дисперсия, среднеквадратическое
отклонение, моменты).
Для охарактеризования рассеяния
наблюдаемых значений количественного
признака выборки вокруг среднего
значения
![]() вводится выборочная
дисперсия.
Выборочной
дисперсией
вводится выборочная
дисперсия.
Выборочной
дисперсией
![]() называют среднее арифметическое
квадратов отклонения наблюдаемых
значений признака от их среднего
значения
.
Если все значения
называют среднее арифметическое
квадратов отклонения наблюдаемых
значений признака от их среднего
значения
.
Если все значения
![]() признака
выборки объема n
различны, то:
признака
выборки объема n
различны, то:
![]() .Если
значения признака
.Если
значения признака
![]() имеют
частоты
имеют
частоты
![]() соответственно, причем
соответственно, причем
![]() ,
то:
,
то:
![]() .Выборочное
среднее
является несмещенной состоятельной
оценкой генерального среднего. В то же
время, несмещенной состоятельной
оценкой генеральной дисперсии оказывается
не выборочная дисперсия
,
а так называемая «исправленная»
выборочная
дисперсия,
равная
.Выборочное
среднее
является несмещенной состоятельной
оценкой генерального среднего. В то же
время, несмещенной состоятельной
оценкой генеральной дисперсии оказывается
не выборочная дисперсия
,
а так называемая «исправленная»
выборочная
дисперсия,
равная
![]() .
.
