[Править]Определение

Если приготовлены несколько идентичных копий системы в данном состоянии, то измеренные значения координаты и импульса будут подчиняться определённому распределению вероятности — это фундаментальный постулат квантовой механики. Измеряя величину среднеквадратического отклонения Δx координаты и среднеквадратического отклонения Δp импульса, мы найдем что:

,

где   — приведённая постоянная Планка. В некоторых случаях «неопределённость» переменной определяется как наименьшая ширина диапазона, который содержит 50 % значений, что, в случае нормального распределения переменных, приводит для произведения неопределённостей к большей нижней границе  . Отметьте, что это неравенство даёт несколько возможностей — состояние может быть таким, что x может быть измерен с высокой точностью, но тогда p будет известен только приблизительно, или наоборот p может быть определён точно, в то время как x — нет. Во всех же других состояниях, и x и p могут быть измерены с «разумной» (но не произвольно высокой) точностью.

В повседневной жизни мы обычно не наблюдаем неопределённость потому, что значение   чрезвычайно мало.

17.Уравнение Шредингера

Наличие волновых свойств у микрочастиц делает уравнение Ньютона, описывающее движение, непригодным для описания движения микрочастиц. Их движение опис. волновыми формами.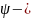 функцию определяют, решив основное уравнение нерелятев. квантовой механики. Его вывел Шредингер в 1926г. Оно, как и II З. Н. постулируется, а не выводится:

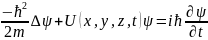(1)

Где m-масса частицы; 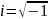–мнимая единица; ∆=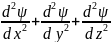 –Оператор Лапласа; -пот. энергия частицы в силовом поле,в котором она движется.Это уравнение справедливо для любой частицы, движущейся со скор. V.

Уравн. Шредингера связывает ф. U с m-массой, её полной энергией Е и U- пот.энергией. Пот. Энергия опр. Силовым полем, в кот. Находится частица, и для стационарного случая не зав. от времени t:

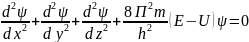(2)

По своему смыслу 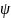должна удовл. след.требованиям: быть однозначной, непрерывной, конечной во всём пространстве, иметь непрерывные производные. Для объективно сущ. частицы должно вып. условие нормировки, т. е. вероятность нахождения частицы в пространстве где-либо равна 1.

В тех местах. Где частица не может оказаться 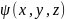=0. Все эти условия назыв. стандартными.

Если частица перемещается вдоль оси Х, то уравн. Шр. имеет вид:

(в уравн. входит полная энергия частицы Е):

(3)

18. Линейный гармонический осциллятор

В общем случае на квантование энергии частицы влияет форма потенциальной ямы. Пусть частица, массой m, удерживается в опред. Области пространства под действием силы F= - kx.

(1)

Где 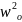= 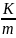– собств. циклическая частота; К-коэф. квазиупругой силы

Уравнение Шредингера для этой частицы, являющейся линейным гармоническим осциллятором:

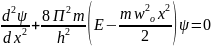(2)

Потенц. ямой для лин. гарм. осцил. будет область, ограниченная кривой пот.эненргии.

Решение уравнения (2) позволит определить полную энергию гармон. осцил.: E_п=hν(n­­+1/2) (3) где ν=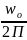 ;n=1,2,3…

Из (3) вытекает, что осциллятор имеет дискретный спектр значений энергии, расп. на одинаковых расстояниях др. от др.

Наименьшая энергия Е_о = ½ hν_o , которую может иметь гармонич осциллятор назыв нулевой (Е_о). Е_оникогда не обратится в 0.

Существование нулевой энергии подтверждается при изучении рассеивания света кристаллами, расп. в узлах кристаллической решётки. Установлено, что при уменьшении температуры, интенсивность рассеянного света не убывает ниже некоторого предела. Т. о. при сверхнизких Т сущЕ_о.