11. Частица, заключенная в одномерном ящике.

Р ассмотрим частицу, которая должна двигаться вдоль прямой (по оси Х), между точками х(0) и х(L). С точки зрения классической физики, частица непрерывно совершает прямолинейные движения в направлении +х и –х, в этом случае не существует никаких ограничений на энергию, которая может иметь частица. Энергия и импульс связаны соотношением: 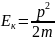. Рассмотрим квантовую частицу, движущуюся в аналогичных условиях (электрон). Мы должны учесть волновые свойства частицы и исследовать условия, которые накладывает на волновую функцию ψ(х) наличие стенок. Решение этой задачи совпадает с решением задачи о стоячих волнах в струе. При этом существенно, что волновая функция частицы должна обращаться в 0, при х=0 и х=Х, т.к. частица не имеет право покинуть ящик пропорциональна вероятности найти частицу в какой-либо точке), следовательно ψ(х)=0 везде вне ящика, значит и на его стенках. Это означает, что в ящике должны быть помещены стоячие волны де Бройля, при условии, что на длине 2L укладывается целое число длин волн, следовательно, длины волн должны удовлетворять соотношению: nλ=2L, где n=1, 2, 3 и т.д. Вероятность обнаружить частицу в какой-либо точке внутри ящика пропорциональна 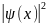. Видны 4 области, где можно с большой вероятностью обнаружить частицу, и области, где эта вероятность равна 0, причем не только на стенках, но и внутри ящика. Этот результат протеворечит классическим представлениям.

12. Разрешенное значение частицы в ящике.

В ычислим энергии соответствующих разрешенным длинам волн, использую соотношение де Бройля и формулу nλ=2L. Разрешенные импульсы равны: , где n = 1,2,3,… А соответствующие им энергии равны . Получили, что частица в ящике может обладать определенными значениями энергии. В отличие от классической, в кот.зависимость E(P) выражалась сплошной параболой, квантовый результат говорит о том, что на параболе доступны только отдельные точки. Квантовые частицы, заключ. в ящике могут обладать только дискретными значениями энергии. Они показаны горизонтальными линиями с точками. Второй важный результат: частице запрещено иметь нулевую кин. энергию. Т.е. частица внутри ящика не может находиться в покое. Т.к. она имела бы р=0 и значит бесконечно большую длину волны де Бройля, которую невозможно уместить в ящике. Частицу в ящике можно считать находящейся в потенц. яме. Т.е. внутреннее ящика соответствует конечная потенциальная энергия, а стенка и внешняя область бесконечно большая потенциальная энергия. Поэтому частица никогда не может покинуть ящик, т.к. у нее должно быть бесконечно большая энергия. Реальные потенц. ямы не имеют бесконечно высоких стенок. И частицы, приобретя достаточную энергию могут покинуть их. Например, в металле электроны, находятся в потенц. яме, ноесли они получают достаточную энергию фотонов ультрафиолетового света, то электроны могут вылетать из металла, что и в фотоэффекте. Энергия Е1 сравнима по величине с энергией электрона в атоме водорода. На самом деле электрон в ящике лишь грубая модель атома водорода. Ящик представляет собой прямоугольную потенц яму, тогда как в атоме водорода электрон движется в потенц яме обратно кулоновской модели. U(х) – потенц энергия, т.е. энергия взаимодействия в обоих случаях – начальное поведение сходно. Поскольку электрон должен описываться стоячей волной, существует лишь определенный набор возможных волн и соответсвующих им энергий.На рисунке показаны 4 низших энергетических уровней. первый в лучае потенциальной ямы с бесконечно высокими стенками и второй- случай в потенц яме, образованной силой электростатич. напряжения.

13. Волновые пакеты.

Рассмотрим движение вдоль оси Х частицы сλ₀. Волновое число частицы . Если импульс точно известен, то мы не знаем ее местонахождение, но в большинстве физических ситуаций, что частица находится в определенной области пространства. Рассмотрим след. волновую функцию в t=0. 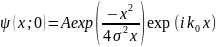Рис. а- график косинусойды с началом не в нуле, второй см рис.

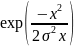На первом рис показана действительная часть этой волновой функции. На втором рис. соответствующее распределение вероятности. Более чем в 50% случаях частицу можно обнаружить в интервале ±σ. представляет собой распределение Гаусса, где σ-среднее квадратическое отклонение, которое называется неопределенностью волны х и обозначается Δх. Такая локальная волна называется волновым пакетом.