9.Великий парадокс.

Парадокс можно устранить предположив, что отдельный фотон после прохожд.через щели S₁ и S₂ способен расщепляться и интерферировать с самим собой. Парадокс усил., если заменить пучок фотонов на пучок электоронов. В природе никогда не наблюд.половины или части электрона, поэтому отд.электрон может пройти лишь через 1 из 2 щелей.Зн.,распр.электронов на экране должно быть суммой распред.,для каждой щели в отд.,нораспр.,хар-ное (S₁+S₂)не имеет место.Вместо этого мы видим интерф.картину для двух щелей.Не происх.ли крушение чистой логики?Ведь все выглядит так,как если бы 100+100=0.Предположим,что в точке А нах.счетчик Гейгера, регистрирующий ежесекундно 100 электронов,когда открыта 1 любая щель.Когда открыты обе щели,счетчик перестает регестрироватьэлектроны,зн.точка А попадает в интерференц.минимум.Если с начала открыть щель S₁,а затем постепенно открывать щель S₂,то вместо увелич.отсчетов от 100 до 200всех наблюд.уменьш.скор.счета от 100 до 0.Каким же образом открыв 2-ой щели влияет на элекроны,кот.прошли через 1-ую щель?Если поместить счетчик Гейгера в точку В,то по мере открыв.2-ой щели,скор.щелиувелич.от 100 до 400 отсчетов в сек.Т.о.100+100=400.Единств.способ объясн.этих парадоксальных результатов сост.всозд.матем.формализма,совместимого с атомизмом и всегда правильно предсказывающее наблюд.интерф.явл.Мат.формализм,спом.кото.устран.парадокс,ставит в соответствие каждой частицы амплитуду вероятности ψ(x,y,z,t),кот.представл.собойфун-циюкоорд.вр.Вер.обнар. частицу в произвольн.моментвр. t в любой точке x,y,zпропорц.интенсивности,т.е. 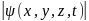². Квадрат модуля использ.,чтобы показ,что ψ-комплексная фун-ция.Онаоблад.св-вами классич. волн-волновая фун-ция.Этафун-цияобознач.ψ и исп.длявычисл.вероятноститого,что частицу или фотон можно обнар.по их взаимод. с в-вом в дан.точке.Волновой функцией ψ(х) нельзя дать классич.(механич.или эл-магн.) толкования-не сущ.того, чтосовершило бы колебание,т.к. эл-магн. Волны свободно распр. в пустом пространстве.Изучая волновые явления,установилось, что дифр.картину от двух щелей можно описать как результат интерф. волн от двух щелей. В точке x=x₀ экрана волн.функция равна ψ(х₀).Вероятносьтого,что электрон попадет в окр.Δх точки х=х₀,равна 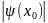²Δx. Если мы имеем две волновых функции ψ₁(х) и ψ₂(х),которые описывают электронные волны,исход.от двух щелевых источников,товероятн.найти электрон в точке х=х₀ или интенсивность 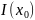потока электронов в этой точке равна: . Для вычисления интенсивности амплитуды ψ₁ и ψ₂, сначала надо сложить, а потом возвести их сумму в квадрат.Т.к.волн.функция имеет знак, и может быть «+» или «-», например: 1)Если ψ₁(х₀) =+2 и ψ₂(х₀)=-2, то =0. 2)Если: ψ₁(х₀) =+2 и ψ₂(х₀)=+2, то .

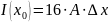10.Свободная частица.

В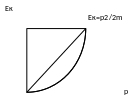 квантовой механике на энергетически свободную частицу, движущуюся в пространстве не накладывается никаких ограничений. Такая частица может иметь любую длину волны и любую кинетическую энергию, которая в нерелятивистском случае определяется выражением: λ=h/p . Видно, что зависимость между кинетической энергией и импульсом является квадратичной. На рис. представлен вид параболы, каждая точка которой характеризует разрешенную энергию для частицы и соответствующий для частицы разрешенный импульс.