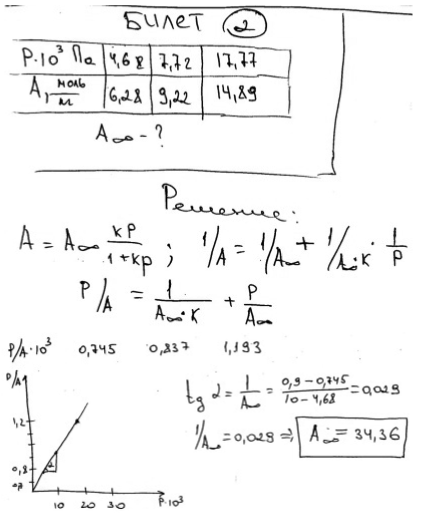
3. В таблице приведены данные по адсорбции паров воды макропористым адсорбентом при комнатой температуре. Пользуясь уравнением Ленгмюра определите емкость адсорбционного монослоя:

P·10-3, Па	А, моль/кг
4,68	6,28
7,72	9,22
17,77	14,89

Экзаменационный билет № 3

1. Метод избытков Гиббса. Вывод фундаментального адсорбционного уравнения Гиббса. Гиббсовская адсорбция. Частное выражение уравнения Гиббса. Поверхностная активность, поверхностно-активные и поверхностно-инактивные вещества.

Для описания термодинамики поверхностных явлений применяют два метода: метод избыточных величин Гиббса и метод «слоя конечной толщины».

Ч тобы не определять границы поверхностного слоя (поверхности разрыва по Гиббсу), Гиббс предложил относить все изменения термодинамических параметров в слое в сравнении с параметрами объемной фазы к разделяющей поверхности, не имеющей объема или толщины (метод избыточных величин Гиббса). При таком рассмотрении поверхность характеризуется избыточными термодинамическими параметрами, непосредственно отражающими проявление поверхностной энергии. Объемные фазы считаются однородными вплоть до разделяющей поверхности. В соответствии с методом избыточных величин энергия Гиббса системы равна сумме энергий Гиббса G₁ и G₂ объемных фаз 1, 2 и поверхностной энергии Гиббса σs, которая является избыточной:

Характеристика величины адсорбции определяющаяся избытком вещества в поверхностном слое определенной толщины по сравнению с его количеством в таком же объеме фазы, также отнесенным к единице площади поверхности или единице массы адсорбента, называется гиббсовской адсорбцией и обозначается буквой гамма Г (метод избыточных величин Гиббса).

Объединенное уравнение первого и второго начал термодинамики для внутренней энергии поверхности с учетом поверхностной и химической энергии имеет вид (объем поверхностного слоя равен нулю)

Так как внутренняя энергия поверхности пропорциональна экстенсивным величинам, то

и ее полный дифференциал от тех же переменных запишется следующим образом:

Подставляя значение dU, получим:

Д ля условия постоянства температуры это соотношение принимает вид

Разделив полученное уравнение на площадь поверхности, получим:

Данное уравнение называют фундаментальным адсорбционным уравнением Гиббса.

Для адсорбции одного конкретного вещества при постоянных химических потенциалах других веществ полученное уравнение можно записать относительно частной производной для данного компонента:

Принимая во внимание, что

Для гиббсовской адсорбции это выражение принимает вид

Для растворенного вещества это выражение переходит в широко используемые адсорбционные уравнения Гиббса для неэлектролитов

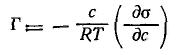
и для электролитов при их диссоциации в полярной фазе и отсутствии ее в поверхностном слое (при неполярной второй фазе):

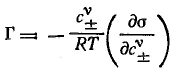
Общее определение поверхностной активности дается соотношением:

которое справедливо как для неэлектролитов, так и для электролитов.

Поверхностная активность, как и гиббсовская адсорбция, может быть положительной и отрицательной. Абсолютное значение и ее знак зависят от природы как адсорбируемого вещества, так и среды (растворителя). Если с увеличением концентрации вещества поверхностное натяжение на границе раздела фаз понижается, то такое вещество называют поверхностно-активным. Для таких веществ

Вещества, повышающие поверхностное натяжение на границе раздела фаз с увеличением концентрации, называют поверхностно-инактивными. Для них