2. Ньютоновские жидкости, уравнения Ньютона и Пуазейля. Методы измерения вязкости. Уравнение Эйнштейна для вязкости дисперсных систем, границы применения.

Ж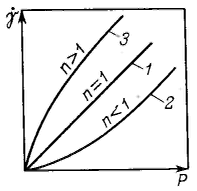 идкообразные тела классифицируют на ньютоновские и неньютоновские жидкости. Ньютоновскими жидкостями называют системы, вязкость которых не зависит от напряжения сдвига и является постоянной величиной в соответствии с законом Ньютона: P = η Течение неньютоновских жидкостей не следует закону Ньютона, их вязкость зависит от напряжения сдвига. В свою очередь, они подразделяются на стационарные, реологические свойства которых не изменяются со временем, и нестационарные, для которых эти характеристики зависят от времени. Среди неньютоновских стационарных жидкостей различают псевдопластические и дилатантные. Типичные зависимости скорости деформации жидкообразных тел от напряжения (кривые течения, или реологические кривые) представлены на рисунке.

Общую зависимость напряжения сдвига от скорости деформации можно выразить в виде степенной функции:

Если n = 1, то данное соотношение переходит в уравнение Ньютона.

Это двухпараметрическое уравнение известно под названием математической модели Оствальда — Вейля. Ньютоновская вязкость η неньютоновской стационарной жидкости определяется уравнением .

Если n = 1, жидкость является ньютоновской и константа k совпадает со значением ньютоновской вязкости (кривая 1). Таким образом, отклонение n от единицы характеризует степень отклонения свойств жидкости от ньютоновских.

Основы теории вязкости разбавленных лиозолей (суспензий) были заложены Эйнштейном. Он исходил из гидродинамических уравнений для систем макроскопических твердых сферических частиц,, которые при сдвиге приобретают дополнительное вращательное движение. Возникающее при этом рассеяние энергии является причиной возрастания вязкости. Эйнштейном была установлена связь между вязкостью дисперсной системы η и объемной долей дисперсной фазы φ:

Формула Эйнштейна не учитывает наличия у частиц поверхностных слоев, таких как адсорбционные, сольватные и двойные электрические. Оно было получено в предположении отсутствия взаимодействия между частицами дисперсной фазы, поэтому оно справедливо только для разбавленных растворов. С увеличением концентрации дисперсной фазы взаимодействие частиц возрастает, и его необходимо учитывать.

Одним из приборов для определения вязкости является капиллярный вискозиметр. При измерении капиллярным вискозиметром, вязкость рассчитывают по уравнению Пуазейля:

Для исследования вязкости неньютоновских жидкостей используется ротационный вискозиметр.

3. Рассчитайте ζ-потенциал по данным электроосмоса через корундовую (Аl₂О₃) мембрану: при силе тока 0,015 A за 60 секунд перенесено 1,2 мл раствора, удельная электропроводимость которого χ_V = 0,012 Ом^-1·м^-1, поверхностная проводимость χ_S = 0,005 Ом^-1·м^-1, η = 10^-3 Па·с, ε = 81, ε₀ = 8,85·10^-12 Ф/м.

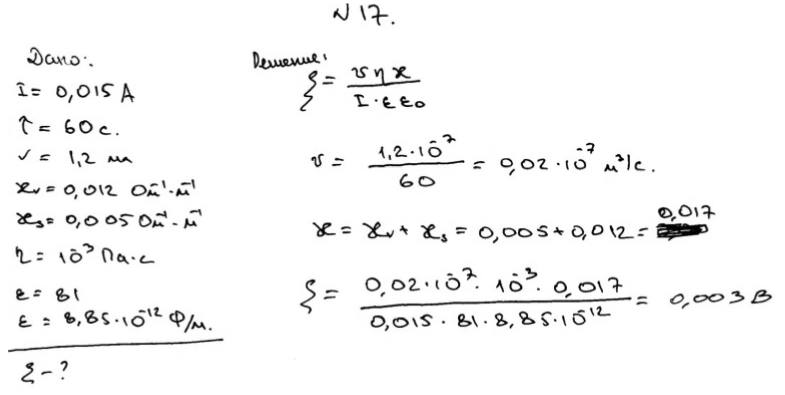
Экзаменационный билет № 18

1. Адгезия, смачивание и растекание жидкостей как поверхностные явления, общность и различие этих явлений. Условия растекания, коэффициент растекания по Гаркинсу. Влияние ПАВ на смачивание и растекание.

Адгезия, смачивание и растекание относятся к межфазным взаимодействиям, которые происходят между конденсированными фазами. Межфазное взаимодействие, или взаимодействие между приведенными в контакт поверхностями конденсированных тел разной природы, называют адгезией (прилипанием).

Смачивание— это поверхностное явление, заключающееся во взаимодействии жидкости с твердым или другим жидким телом при наличии одновременного контакта трех несмешивающихся фаз, одна из которых обычно является газом (воздухом). Степень смачивания количественно характеризуется косинусом краевого угла (угла смачивания), или просто краевым углом (углом смачивания).

Капля жидкости, нанесенная на поверхность, может оставаться на ее определенном участке, и система будет находиться в равновесии в соответствии с законом Юнга, или же растекаться по поверхности. В обоих этих случаях система переходит в состояние с минимальной энергией Гиббса. Если капля не растекается, то, кал было показано выше, краевой угол зависит от соотношения работ адгезии W_а и когезии W_к смачивающей жидкости.

Рассмотрим условия растекания жидкости 2 по поверхности 3. Изменение энергии Гиббса можно записать следующим пбразом:

Для самопроизвольного процесса dG<0 и ds>0:

Если разность заменить выражением из уравнения Дюпре, то получим или

Разницу между левой и правой частями этих неравенств называют коэффициентом растекания f по Гаркинсу: или

При положительном значении коэффициента f жидкость растекается по поверхности, при отрицательном — нe растекается.

Введение ПАВ уменьшает работу когезии (поверхностное натяжение) жидкости а значит, как следует из уравнения Дюпре-Юнга, увеличивает смачивание. Лучше смачивает та жидкость, которая имеет меньшее поверхностное натяжение или работу когезии.