Экзаменационный билет № 11

1. Количественные характеристики пористых материалов: пористость, удельная поверхность, размер пор. Пористые тела корпускулярной, кристаллической и губчатой структуры, методы их получения. Классификации пор по Дубинину и теория адсорбции.

Пористые тела — это твердые тела, внутри которых имеются поры, обусловливающие наличие внутренней межфазной поверхности. Поры могут быть заполнены газом или жидкостью.

Высокодисперсные пористые неорганические материалы, в частности, адсорбенты и катализаторы, получают в основном двумя методами. Один из них заключается в синтезе гидрозоля с последующей его коагуляцией для образования геля; гель высушивают. Частицы дисперсной фазы (корпускулы) в результате этих операций срастаются с образованием твердого каркаса. Так как частицы золя высокодисперсны, то получаемый пористый материал имеет большую удельную поверхность. Таким методом получают адсорбенты корпускулярной структуры.

Второй метод получения высокодисперсных пористых адсорбентов и катализаторов заключается в обработке крупнопористых материалов агрессивными газами или жидкостями. При такой обработке получаются пористые тела губчатой структуры.

Наибольшее распространение получила классификация пористых тел, предложенная M. M. Дубининым. По этой классификации за основу приняты размеры пор и механизм протекающих в них адсорбционных процессов. По классификации M. M. Дубинина пористые тела делятся на макропористые, переходнопористые, микропористые в зависимости от линейного размера, под которым понимают полуширину для щелевидной поры или радиус для сферической или цилиндрической поры.

Макропористые тела имеют поры радиусом больше 100,0 — 200,0 нм, удельная поверхность макропористых тел находится в пределах 0,5 — 2 м²/г. В связи с тем, что такие поры намного больше адсорбируемых молекул, то их стенки по сравнению с молекулами можно рассматривать как ровные поверхности, поэтому для макропористых тел применима обобщенная теория адсорбции Ленгмюра.

Переходнопористые тела (или капиллярно-пористые, или мезопористые) имеют размеры пор в пределах от 1,5 до 100,0 — 200,0 нм их удельная поверхность составляет от 10 до 500 м²/г. Ha стенках этих пор при малых давлениях происходит полимолекулярная адсорбция паров, которая с увеличением давления заканчивается капиллярной конденсацией.

Микропористые тела обладают порами, соизмеримыми с размерами адсорбируемых молекул. Радиусы пор лежать в пределах от 0,5 до 1,5 нм. Удельная поверхность таких тел 500 — 1000 м²/г и выше. Отличительной чертой микропор является настолько близкое расположение противоположных стенок, что их поля поверхностных сил перекрываются и они действуют во всем объеме микропор.

Одной из основных характеристик пористой структуры тела является пористость — отношение объема пор V_п к общему объему тела V_общ:

Если принять, что поры в пористых телах и порошках имеют правильную форму, то их размеры можно оценить, зная пористость и удельную поверхность:

Для определения пористости и удельной поверхности пористых тел широко используются адсорбционные методы.

2. Лиофобные дисперсные системы. Факторы агрегативной устойчивости лиофобных систем. Быстрая и медленная коагуляция. Кинетика коагуляции по Смолуховскому (вывод уравнения). Определение константы скорости и времени половинной коагуляции. Зависимость числа частиц разного порядка от времени.

Все дисперсные системы в зависимости от механизма процесса их образования по классификации П. А. Ребиндера подразделяют на лиофильные, которые получаются при самопроизвольном диспергировании одной из фаз (самопроизвольное образование гетерогенной свободнодисперсной системы), и лиофобные, получающиеся в результате диспергирования и конденсации с пересыщением (принудительное образование гетерогенной свободноднсперсной системы).

Различают следующие термодинамические и кинетические факторы устойчивости дисперсных систем:

1. Электростатический фактор заключается в уменьшении межфазного натяжения вследствие возникновения двойного электрического слоя на поверхности частиц в соответствии с уравнением Липпмана.

2. Адсорбционно-сольватный фактор состоит в уменьшении межфазного натяжения при взаимодействии частиц дисперсной фазы со средой (благодаря адсорбции и сольватации)

3. Энтропийный фактор, как и первые два относится к термодинамическим. Он дополняет первые два фактора и действует в системах, в которых частицы или их поверхностные слои участвуют в тепловом движении.

4. Структурно-механический фактор является кинетическим. Его действие обусловлено тем, что на поверхности частиц имеются пленки, обладающие упругостью и механической прочностью, разрушение которых требует затраты энергии и времени.

5. Гидродинамический фактор снижает скорость коагуляции благодаря изменению вязкости среды и плотности дисперсной фазы и дисперсионной среды.

6. Смешанные факторы наиболее характерны для реальных систем. Обычно агрегативная устойчивость обеспечивается несколькими факторами одновременно.

Коагуляция протекает в термодинамически неустойчивых (лиофобных) дисперсных системах, и об агрегативной устойчивости таких систем судят по скорости коагуляции.

Смолуховским была рассмотрена кинетика коагуляции монодисперсных золей со сферическими частицами, которые сталкиваются между собой в результате броуновского движения. Критическое расстояние, на котором осуществляется взаимодействие между частицами, принято приблизительно равным сумме радиусов частиц, что соответствует непосредственному их контакту. Согласно представлениям Смолуховского при коагуляции происходят взаимодействия только между двумя частицами, так как вероятность одновременного столкновения большого числа частиц очень мала. Таким образом, сталкиваются частицы одиночные, образуя двойные, одиночные с двойными, двойные друг с другом, тройные с одиночными и т. д. Такое представление процесса коагуляции позволяет формально применить к нему теорию бимолекулярных химических реакций.

Относительное смещение двух частиц. Δ_n—Δ_m с коэффициентом относительной диффузии D_nm связано законом Эйнштейна — Смолуховского:

В соответствии с первым законом Фика поток через сферическую поверхность s выражается уравнением

Интегрируя уравнение данное после разделения переменных в пределах от R_nm до ∞ и соответственно от 0 до ν_n, получим:

Данное уравнение отражает также число столкновении на данной стадии процесса коагуляции, т. е. число частиц, сталкивающихся в единицу времени с одной центральной частицей. Общее число столкновений между частицами в системе в единицу времени в данный момент составляет .

Чтобы рассчитать скорость уменьшения числа частиц в результате коагуляции, т. е. скорость коагуляции, необходимо принять, что все столкновения приводят к агрегации. Необходимо учесть стерический множитель P, учитывающий благоприятные пространственные расположения частиц при столкновении, их форму, размеры. Тогда скорость коагуляции в данный момент времени составит:

Сравнение с уравнением для скорости бимолекулярной реакции , показывает, что константа скорости коагуляции выражается следующим соотношением:

Общее число частиц в результате коагуляции уменьшается. Чтобы определить, каким оно будет через время τ, необходимо провести интегрирование в пределах от ν_∑ = ν₀ при τ = 0 до ν_∑ при τ:

Константу скорости коагуляции теоретически определить трудно, поэтому Смолуховский ввел понятие времени (периода) половинной коагуляции θ — времени коагуляции, в течение которого общая концентрация частиц уменьшается до половины от начальной концентрации первичных (единичных) частиц. Из уравнения общего числа частиц следует: и .

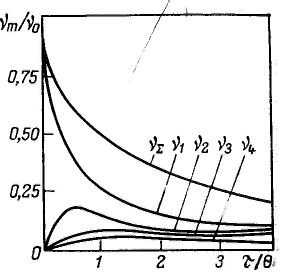О бщее число частиц ν_∑ в единице объема системы представляет собой уменьшающуюся в процессе коагуляции сумму частиц всех порядков:

Этот ряд является суммой геометрической прогрессии со знаменателем

Отсюда легко определить число частиц каждого порядка (m-мерных):

Согласно теории кинетики коагуляции различают быструю и медленную коагуляцию. Для такого разделения можно воспользоваться уравнением константы скорости коагуляции. При быстрой коагуляции все столкновения частиц эффективны, т. е. приводят к слипанию частиц. При медленной коагуляции это утверждение не соблюдается.