16 Элементы теории графов. Метрические характеристики графов.

Ответы в бил 15

17 Релейно-контактные схемы.

Посмотрим теперь как обстоит дело с обратной задачей: построением по функции реализующей ее схемы. Представим функцию в виде ДНФ. Каждой входящей в ДНФ элементарной конъюнкции 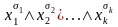поставим в соответствие схему (рис. 1.17), состоящую из последовательно соединенных контактов . Это схема элементарной конъюнкции. На рис. 1.17 и 1.18 величины 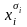обозначены через . После отождествления между собой, с одной стороны, входов всех этих схем, с другой стороны — выходов, получим функцию, соответствующую заданной схеме. Естественно, можно реализовать функцию по схемам также исходя из КНФ. 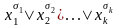Каждой элементарной дизъюнкции поставим в соответствие схему, изображенную на рис. 1.18. Затем последовательно соединим все эти схемы для всех элементарных дизъюнкций, входящих в КНФ, так, чтобы вход последующей схемы совпадал с выходом предыдущей.

Схему, состоящую из одного контакта, называют элементарной. Ясно, что любая 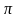-схема может быть получена из элементарных за некоторое число шагов при помощи параллельных и последовательных соединений. Каждому способу построения -схемы из элементарных схем отвечает представление функции проводимости в виде формулы, содержащей только дизъюнкции, конъюнкции и отрицания.

Е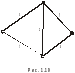 сли контактная схема является -схемой, то ее можно разбить на несколько схем, соединенных либо последовательно, либо параллельно. Обратное тоже верно. Если схема не допускает разбиения на две схемы, соединенные либо последовательно, либо параллельно, она не является -схемой. Для примера рассмотрим схему "мостик" (рис. 1.19), которая не является элементарной. Если две схемы соединены последовательно, то у полученной общей схемы все полюсы, кроме соединяющего, либо не имеют общих контактов ни с входом, ни с выходом всей схемы, либо имеют общий контакт или только с входом, или только с выходом. Очевидно, что какой бы из внутренних полюсов на рис. 1.19 мы не приняли за соединяющий подсхемы, оставшийся полюс будет иметь общий контакт как с входом, так и с выходом схемы. Поэтому схему "мостик" нельзя получить последовательным соединением двух схем.

Рис. 1.19. Схема "мостик"

Если общая схема — результат параллельного соединения двух схем, то ее контакты и полюсы можно разбить на две части так, чтобы либо в одной части содержались контакты, непосредственно соединяющие вход и выход, либо полюсы, входящие в рассматриваемые различные две части схемы и отличные от входа и выхода, не будут иметь общих контактов. Ни первая, ни вторая возможность на схеме рис. 1.19 не может реализоваться. Следовательно, эта схема не является -схемой.

Две контактные схемы называются эквивалентными, если они реализуют одну и ту же булеву функцию или одну и ту же систему функций. Схема называется минимальной, если она содержит наименьшее возможное число контактов среди всех схем, имеющих ту же функцию проводимости.

Рис. 1.20. Примеры релейно-контактных схем

Пример 3. Найти функции, реализуемые схемами на рис. 1.20.

Первые две функции представлены -схемами, поэтому их восстановление довольно просто: а) 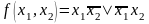 ; б)  .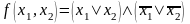

Для последнего пункта (в) составим по формуле (1.12.9) функцию проводимости. Для этого необходимо перечислить все цепи, соединяющие начальный и конечный 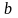полюсы схемы:

.
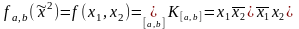
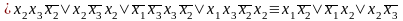