27.Матрицы элементарных преобразований строкМатрица линейного преобразования

В  примере 19.4 было показано, что преобразование -мерного пространства, заключающееся в умножении координатных столбцов векторов на фиксированную матрицу, является линейным преобразованием. В этом разделе мы покажем, что все линейные преобразования конечномерного пространства устроены таким же образом.

Пусть  -- -мерное линейное пространство, в котором задан базис ,  -- линейное преобразование. Возьмем произвольный вектор . Пусть  -- его координатный столбец. Координатный столбец вектора обозначим .

Запишем разложение вектора по базису пространства . Для образа этого вектора получим (19.2)

Векторы имеют какие-то координатные столбцы, обозначим их , , ..., соответственно. В этой записи первый индекс показывает номер координаты, а второй индекс -- номер вектора. Соответственно,

Подставим это выражение в равенство (19.2) и, используя  предложение 14.3, изменим порядок суммирования

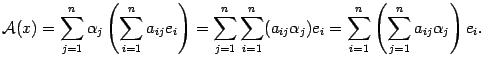
Это равенство означает, что -той координатой вектора служит .

Составим матрицу из координатных столбцов векторов , ...,

Вычислим произведение матрицы на столбец

Мы видим, что -ый элемент столбца совпадает с -ой координатой вектора . Поэтому

(19.3)

Это означает, что в выбранном базисе действие любого линейного преобразования сводится к умножению матрицы на координатный столбец вектора.

Матрица называется матрицей линейного преобразования . Еще раз напомним, как она составлена: первый столбец является координатным столбцом образа первого базисного вектора, второй столбец -- координатным столбцом образа второго базисного вектора и т.д.

        Пример 19.5   Найдем матрицу линейного преобразования из  примера 19.1.

Выберем какой-нибудь базис . Тогда

Следовательно, первый столбец матрицы имеет вид . Аналогично

Второй столбец матрицы имеет вид . В итоге

28.

Определитель произведения квадратных матриц

Определитель произведения квадратных матриц равен произведению определителей сомножителей, то есть .     

Для квадратной матрицы порядка при выполнено соотношение

Определителем квадратной матрицы второго порядка называется число . Определителем квадратной матрицы порядка , , называется число

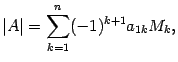
где  -- определитель матрицы порядка , полученной из матрицы вычеркиванием первой строки и столбца с номером

29.Свойства обратных и транспонированных матриц

Cвойства обратных матриц.  Укажем следующие свойства обратных матриц: 1) (A^-1)^-1 = A;  2) (AB)^-1 = B^-1A^-1   3) (A^T)^-1 = (A^-1)^T.   При использовании компьютерной версии “Курса высшей математики” возможно запустить програрамму, которая находит обратную матрицу и подробно описывает весь ход решения для матрицы размера 3х3.   Пример. Дана матрица А = , найти А³. А² = АА =  = ; A³ = = .   Отметим, что матрицы  и  являются перестановочными.  Пример. Вычислить определитель .  = -1  = -1(6 – 4) – 1(9 – 1) + 2(12 – 2) = -2 – 8 + 20 = 10.  = = 2(0 – 2) – 1(0 – 6) = 2. =  = 2(-4) – 3(-6) = -8 + 18 = 10. Значение определителя: -10 + 6 – 40 = -44.

   Определение 14.5   Пусть -- матрица размеров . Тогда транспонированной матрицей называется такая матрица размеров , что , , .         

Транспонированная матрица обозначается или . Операция транспонирования заключается в том, что строки и столбцы в исходной матрице меняются ролями. В транспонированной матрице первым столбцом служит первая строка исходной матрицы, вторым столбцом -- вторая строка исходной матрицы и т.д. Например,

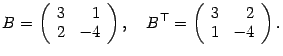
При транспонировании матрицы определитель не меняется, то есть .