5.Извлечение корня из комплексного числа
Заголовок этого
раздела является не совсем точным. Дело
в том, что корень из ненулевого комплексного
числа однозначно определить нельзя. Он
всегда имеет столько значений, какова
его степень. Поэтому в данном разделе
мы будем говорить о решении уравнения
(17.14)
где неизвестным служит
,
а
--
известное комплексное число. Но поскольку
в школе решение этого уравнения
записывалось в виде
,
то, не слишком соблюдая математическую
строгость, можно говорить, что мы будем
извлекать корень
-ой
степени из комплексного числа
.
Итак, решаем уравнение (17.14).
Если
,
то
.
Пусть
.
Запишем число
в
тригонометрической форме:
.
Здесь
и
--
известные величины. Запишем неизвестное
число
в
тригонометрической форме:
.
Здесь
и
--
неизвестны. По формуле Муавра
Таким образом,
Если два комплексных числа равны, то их
модули должны быть равны. Поэтому
.
В этом соотношении
и
--
положительные числа, следовательно
,
где справа стоит обычный арифметический
корень из положительного числа.
Если два комплексных числа равны, то
аргументы у них могут различаться только
на величину, кратную
.
Поэтому
,
.
Отсюда находим, что
В итоге получили:
(17.15)
Значения
,
отличные от указанных в этой формуле,
дадут те же значения
,
которые можно получить при
6.Формулы Эйлера
формула Эйлера
Пусть комплексное число в тригонометрической форме имеет вид . На основании формулы Эйлера выражение в скобках можно заменить на показательное выражение. В результате получим
Эта запись называется показательной формой комплексного числа. Так же, как и в тригонометрической форме, здесь , .
Пример 17.8 Комплексное число записано в показательной форме
Найдите его алгебраическую форму.
Решение. По формуле Эйлера
Итак, алгебраическая форма числа:
.
С помощью формулы Эйлера можно определить
показательную функцию комплексного
аргумента. Пусть
.
Тогда
Например,
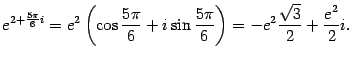
Заменим в формуле Эйлера
на
.
Получим:
С учетом свойств тригонометрических функций имеем:
Сложив последнюю формулу с формулой Эйлера, получим:
Откуда
Аналогично, с помощью вычитания, можно
получить формулу
С помощью формулы для косинуса вычислим,
например,
:
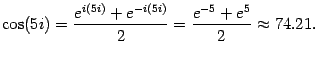
Таким образом, в комплексной области
модуль косинуса может быть и больше 1.
Более того, в комплексной области функции
и
,
определяемые с помощью формул (17.11)
и (17.12),
являются неограниченными функциями.
Действительно, из этих формул мы получаем:
7.Действия над комплексными числами в показательной форме.
Показательная и тригонометрические функции в области комплексных чисел связаны между собой формулой (17.10)
которая носит название формулы Эйлера. Обосновать ее можно с помощью теории степенных рядов. Эта теория будет изложена в курсе математического анализа.
Пусть комплексное число в тригонометрической форме имеет вид . На основании формулы Эйлера выражение в скобках можно заменить на показательное выражение. В результате получим
Эта запись называется показательной формой комплексного числа. Так же, как и в тригонометрической форме, здесь , .
Пример 17.8 Комплексное число записано в показательной форме
Найдите его алгебраическую форму.
Решение. По формуле Эйлера
Итак, алгебраическая форма числа: .
С помощью формулы Эйлера можно определить показательную функцию комплексного аргумента. Пусть . Тогда
Например,
Заменим в формуле Эйлера на . Получим:
С учетом свойств тригонометрических функций имеем:
Сложив последнюю формулу с формулой Эйлера, получим:
Откуда (17.11)
Аналогично, с помощью вычитания, можно получить формулу (17.12)
С помощью формулы для косинуса вычислим, например, :
Таким образом, в комплексной области модуль косинуса может быть и больше 1. Более того, в комплексной области функции и , определяемые с помощью формул (17.11) и (17.12), являются неограниченными функциями. Действительно, из этих формул мы получаем: (17.13)
Так как гиперболические косинус и синус являются неограниченными функциями, то и тригонометрические функции косинус и синус являются неограниченными функциями (в комплексной области).
Отметим также, что формулы (17.13) объясняют, почему для гиперболических функций многие соотношения очень похожи на соотношения между тригонометрическими функциями, например, основное тригонометрическое тождество, формулы двойного аргумента.
9.
Определители второго и третьего порядков. Свойства определителей.
3.1.1. Определители второго порядка
Таблица вида
называется квадратной матрицей второго порядка.
Соответствующие элементы а11, а12, а21, а22 называются элементами матрицы.
Элементы Матрицы образуют ее строки и столбцы. Для обозначения элемента матрицы используют двойной индекс. Первый индекс указывает номер строки, а второй - номер столбца, на пересечении которых находится элемент. Так, элемент aik расположен на пересечении i-ой строки и k-го столбца.
Определителем второго порядка, соответствующим данной матрице, называется число, обозначаемое символом
и определяемое равенством det А = а11а22 - а12а21.
Диагональ, образованная элементами а11 и а22 называется главной.
Диагональ, образованная элементами а12 и а21 называется побочной.
Таким образом, чтобы вычислить определитель второго порядка, надо из произведения элементов главной диагонали вычесть произведение элементов побочной диагонали.
3.1.2. Определители третьего порядка
Таблица вида
называется квадратной матрицей третьего порядка.
Соответствующие элементы а11, а12, а13, а21, а22, а23, а31, а32, а33 называются элементами матрицы.
Элементы Матрицы образуют ее строки и столбцы. Для обозначения элемента матрицы используют двойной индекс. Первый индекс указывает номер строки, а второй - номер столбца, на пересечении которых находится элемент. Так, элемент aik расположен на пересечении i-ой строки и k-го столбца.
Определителем третьего порядка, соответствующим данной матрице, называется число, обозначаемое символом
и определяемое равенством det А = а11а22а33 + а12а23а31 + а13а21а32 - а31а22а13 - а21а12а33 - а11а32а23.
Диагональ, образованная элементами а11, а22 и а33 называется главной.
Диагональ, образованная элементами а31, а22 и а13 называется побочной.
Чтобы запомнить правило вычисления определителя третьего порядка, достаточно мысленно построить так называемую "звезду Давида". Делается это следующим образом:
Здесь указана звезда для положительных элементов. Находится произведение элементов по главной диагонали и по углам треугольников, одна из сторон каждого из которых параллельна главной диагонали. Всего три произведения по три элемента. Затем эти произведения суммируются (см. в определении).
З
десь
указана звезда для отрицательных
элементов. Находится произведение
элементов по побочной диагонали и по
углам треугольников, одна из сторон
каждого из которых параллельна побочной
диагонали. Всего три произведения по
три элемента. Затем эти произведения
суммируются и отнимаются от суммы
произведений положительных элементов
(см. в определении).
3.1.4. Свойства определителей
1. Величина определителя не изменится, если его строки и столбцы поменять ролями:
2. При перестановке двух столбцов (строк) определитель меняет знак на противоположный:
3. Общий множитель элементов какой-нибудь строки (какого-нибудь столбца) может быть вынесен за знак определителя:
4. Если все элементы некоторого столбца (некоторой строки) равны нулю, то сам определитель равен нулю:
5. Если элементы двух столбцов (строк) определителя пропорциональны, то определитель равен нулю:
С л е д с т в и е. Если определитель имеет два одинаковых столбца (две одинаковых строки), то он равен нулю:
6. Свойство линейной комбинации параллельных рядов определителя. Определитель не изменится, если к элементам одного столбца (одной строки) прибавить соответствующие элементы другого столбца (другой строки), умноженные на одно и то же число:
7. Определитель равен сумме произведений элементов любой его строки (либо его столбца) на их алгебраические дополнения.
8. Сумма произведений элементов какой-нибудь строки (какого-нибудь столбца) на алгебраические дополнения другой строки (другого столбца) равна нулю.
14.
Определители третьего порядка. Теоремы разложения и аннулирования.
Таблица вида
называется квадратной матрицей третьего порядка.
Соответствующие элементы а11, а12, а13, а21, а22, а23, а31, а32, а33 называются элементами матрицы.
Элементы Матрицы образуют ее строки и столбцы. Для обозначения элемента матрицы используют двойной индекс. Первый индекс указывает номер строки, а второй - номер столбца, на пересечении которых находится элемент. Так, элемент aik расположен на пересечении i-ой строки и k-го столбца.
Определителем третьего порядка, соответствующим данной матрице, называется число, обозначаемое символом
и определяемое равенством det А = а11а22а33 + а12а23а31 + а13а21а32 - а31а22а13 - а21а12а33 - а11а32а23.
Диагональ, образованная элементами а11, а22 и а33 называется главной.
Диагональ, образованная элементами а31, а22 и а13 называется побочной.
Чтобы запомнить правило вычисления определителя третьего порядка, достаточно мысленно построить так называемую "звезду Давида". Делается это следующим образом:
Здесь указана звезда для положительных элементов. Находится произведение элементов по главной диагонали и по углам треугольников, одна из сторон каждого из которых параллельна главной диагонали. Всего три произведения по три элемента. Затем эти произведения суммируются (см. в определении).
З десь указана звезда для отрицательных элементов. Находится произведение элементов по побочной диагонали и по углам треугольников, одна из сторон каждого из которых параллельна побочной диагонали. Всего три произведения по три элемента. Затем эти произведения суммируются и отнимаются от суммы произведений положительных элементов (см. в определении).
15.
Определители произвольного порядка, их вычисление.
Определение.
Определителем квадратной матрицы
А=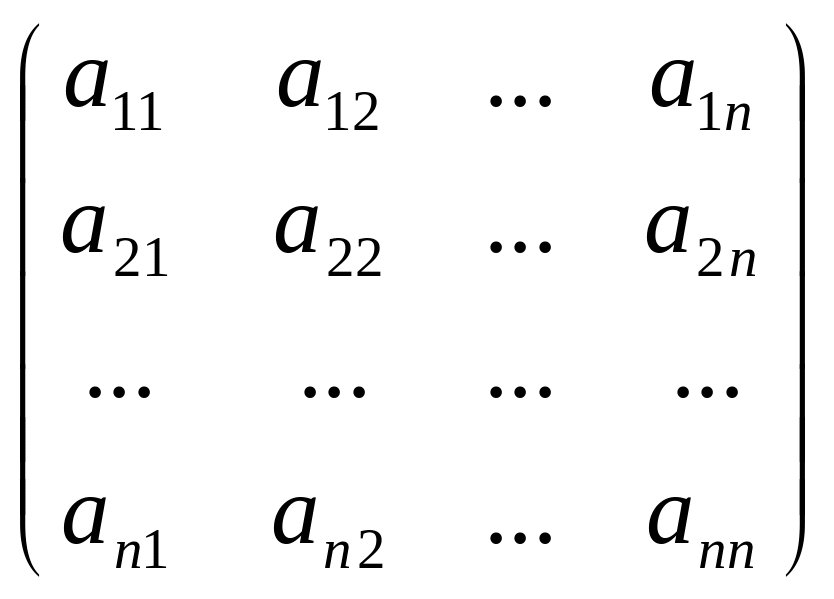
называется число, которое может быть
вычислено по элементам матрицы по
формуле:
det
A =
,
где (1)
М1к – детерминант матрицы, полученной из исходной вычеркиванием первой строки и k – го столбца. Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов.
Ф
ормула
(1) позволяет вычислить определитель
матрицы по первой строке, также справедлива
формула вычисления определителя по
первому столбцу:
det
A =
(2)
Вообще говоря, определитель может вычисляться по любой строке или столбцу матрицы, т.е. справедлива формула:
detA =
,
i = 1,2,…,n.
(3)
Очевидно, что различные матрицы могут иметь одинаковые определители.
Определитель единичной матрицы равен 1.
Для указанной матрицы А число М1к называется дополнительным минором элемента матрицы a1k. Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах.
Определение. Дополнительный минор произвольного элемента квадратной матрицы aij равен определителю матрицы, полученной из исходной вычеркиванием i-ой строки и j-го столбца.
25.
Теорема Крамера
Теорема. Система из n уравнений с n неизвестными
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
xi = i/, где
= det A, а i – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.
i
=
Пример.
A =
;
1=
;
2=
;
3=
;
x1 = 1/detA; x2 = 2/detA; x3 = 3/detA;