17. Ранг матрицы. Теорема об элементарных преобразованиях матрицы.
1. Рангом матрицы А называется такое целое число R, что среди миноров порядка R этой матрицы найдётся хотябы один не равный нулю, а все миноры порядка R+1, если такие существуют - равны нулю. Лемма: Если в матрице А все миноры каждого порядка равны нулю, то все миноры большего порядка тоже равны нулю. 2. Элементарными преобразованиями матрицы называются следующие преобразования: прибавление к одной строчке(столбцу) другой строчки(столбца) переставление строк(столбцов). Лемма: При транспорировании матрицы ранг не меняется. Теорема 1: Элементарные преобразования матрицы не меняют её ранга. Теорема 2: Элементарным преобразованиям строк матрицы А соответствуют равносильные преобразования системы уравнений матрицы. Теорема 3: При помощи элементарного преобразования строк - любую мматрицу m на n можно привести к следующему виду: Некоторые R столбцов совпадают с первыми R столбцами единичной матрицы порядка m. Если R<m то последние (m-R) строк состоят из нулей.
Пример:
Решить системы
уравнений.
1.
Найдем матрицу обратную матрице A.
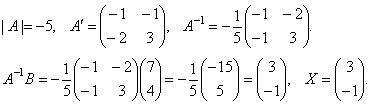Таким
образом, x = 3, y = – 1.
21 Метод Гаусса приведения матрицы к упрощённому виду
Суть метода заключается
в последовательном исключении неизвестных.
Рассмотрим систему линейных уравнений:
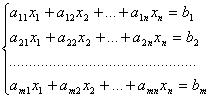Разделим
обе части 1–го уравнения на a11 <> 0,
затем: 1) умножим на а21 и вычтем из второго
уравнения 2) умножим на а31 и вычтем из
третьего уравнения и т.д.
Получим:
,
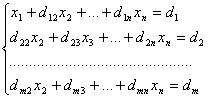где d1j = a1j/a11, j = 2, 3, …, n+1.
dij = aij – ai1d1j i = 2, 3, … , n; j = 2, 3, … , n+1. Далее
повторяем эти же действия для второго
уравнения системы, потом – для третьего
и т.д.
Допускаются следующие элементарные преобразования: 1)Перестановка строк расширенной матрицы. 2)Умножение i-й строки расширенной матрицы на число альфа, не равное нулю. 3)Прибавление к i-й строке расширенной матрицы j-ю строку умноженную на заданное число альфа.
рассмотрим некоторые ситуации: ( 0 0 0 ... 0 I bi ) - нет решений две одинаковые строчки. - одну из них можно вычеркнуть. если в строчке стоят одни нули, то мы её вычёркиваем.
Пример: Решить систему
методом Гаусса.
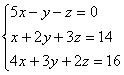Составим
расширенную матрицу системы.
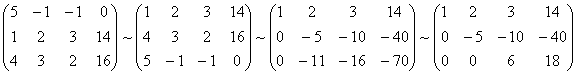Таким
образом, исходная система может быть
представлена в виде:
,
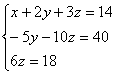откуда получаем: z = 3; y = 2; x = 1. Полученный
ответ совпадает с ответом, полученным
для данной системы методом Крамера и
матричным методом.
21. Теорема о базисном миноре.
Теорема: В произвольной матрице А каждый столбец (строка) является линейной комбинацией столбцов (строк), в которых расположен базисный минор.
Таким образом, ранг произвольной матрицы А равен максимальному числу линейно независимых строк (столбцов) в матрице.
Если А- квадратная матрица и detA = 0, то по крайней мере один из столбцов – линейная комбинация остальных столбцов. То же самое справедливо и для строк. Данное утверждение следует из свойства линейной зависимости при определителе равном нулю.
Пример: Определить ранг
и найти базисные миноры матрицы
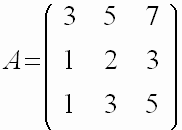Решение.
Сложим соответствующие элементы первой
и третьей строк, а затем разделим на 4
элементы первой строки. Из элементов
первой строки вычтем соответствующие
элементы второй строки, после чего
вычеркнем первую строку:
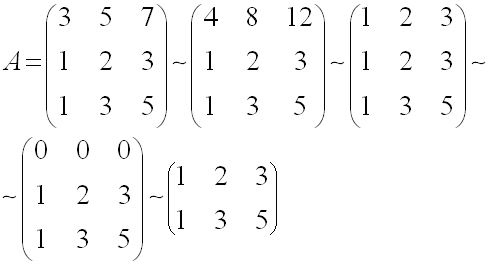r(A)=2.
А базисными минорами являются три минора
второго порядка этой матрицы, отличные
от нуля:
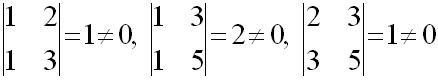
22.
Теорема о ранге матрицы.
Теорема о ранге.
Определение 4.3. Базисным минором матрицы называется любой ее ненулевой минор, порядок которого равен рангу матрицы.
Определение 4.4. Строки (столбцы) матрицы называются линейно зависимыми, если существует их линейная комбинация, не все коэффициенты в которой равны 0, равная нулевой строке (столбцу).
В противном случае строки (столбцы) называются линейно независимыми.
Замечание. Можно доказать, что необходимым и достаточным условием линейной зависимости строк матрицы является то, что одна из них является линейной комбинацией остальных.
Теорема 4.1. Строки и столбцы матрицы, элементы которых входят в базисный минор, линейно независимы. Любая строка (столбец) матрицы является линейной комбинацией этих строк (столбцов).
Доказательство (для строк).
1. Если бы базисные строки были линейно зависимыми, то с помощью эквивалентных преобразований из них можно было бы получить нулевую строку, что противоречит условию, что базисный минор не равен 0.
2. Строка, входящая в базисный минор, является линейной комбинацией его строк, в которой коэффициент при данной строке равен 1, а остальные коэффициенты равны 0.
Докажем это свойство для строки, не входящей в базисный минор.
Добавим к базисному минору эту строку (пусть ее номер – k) и любой столбец матрицы (пусть его номер – j). Затем разложим полученный определитель, равный 0 (так как его порядок больше ранга матрицы) по j-му столбцу:
Поскольку
является
базисным минором,
поэтому, разделив полученное равенство
на
,
найдем, что
для всех j=1,2,…,n,
где
.
Следовательно, выбранная строка является
линейной комбинацией базисных строк.
Теорема доказана.
23.
Теорема Кронекера-Капелли
Теорема: Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
RgA = RgA*.
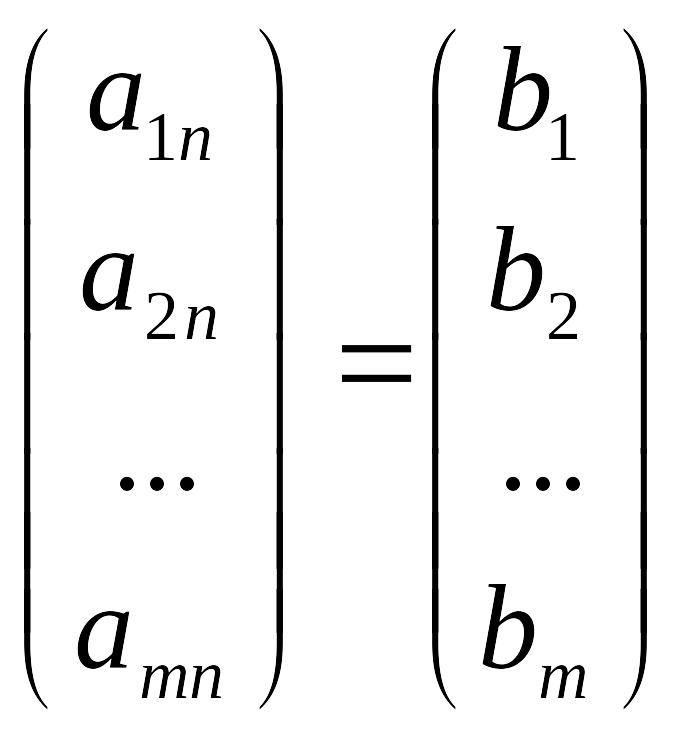
Очевидно, что система (1) может быть записана в виде:
x1
+
x2
+
… + xn
Доказательство.
1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход АА* не изменяют ранга.
2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.
Пример. Определить совместность системы линейных уравнений:
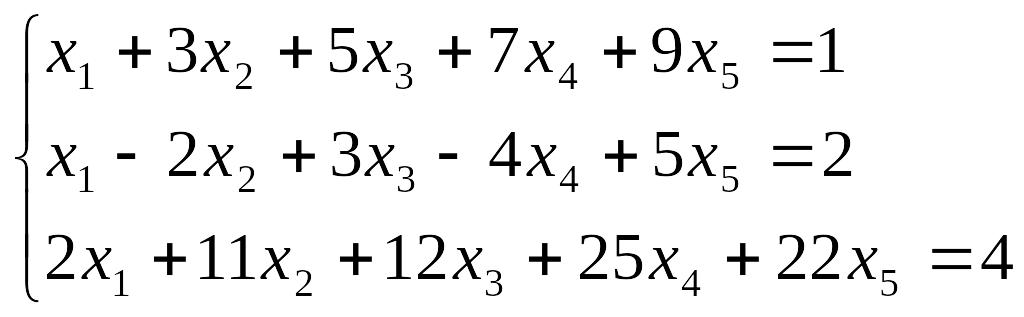
A
=
~
.
RgA
= 2.
A*
=
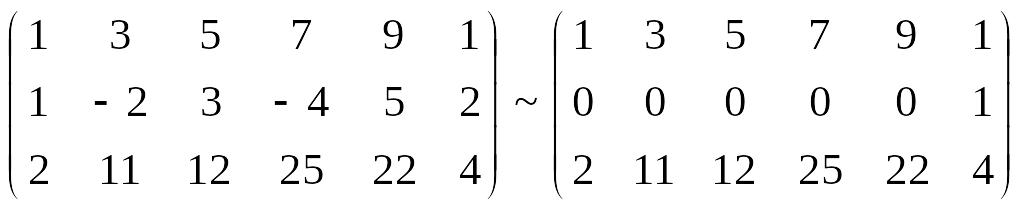RgA*
= 3.
Система несовместна.
Пример. Определить совместность системы линейных уравнений.
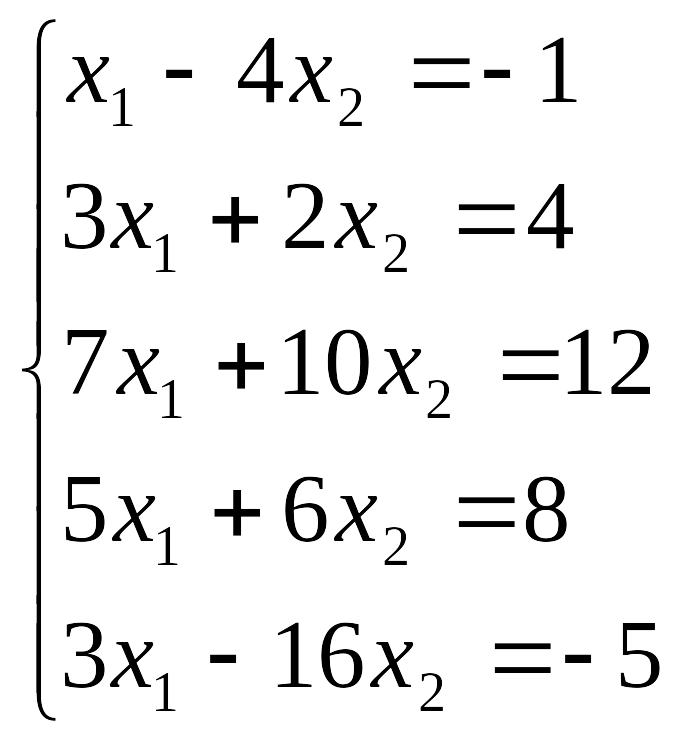А =
;
=
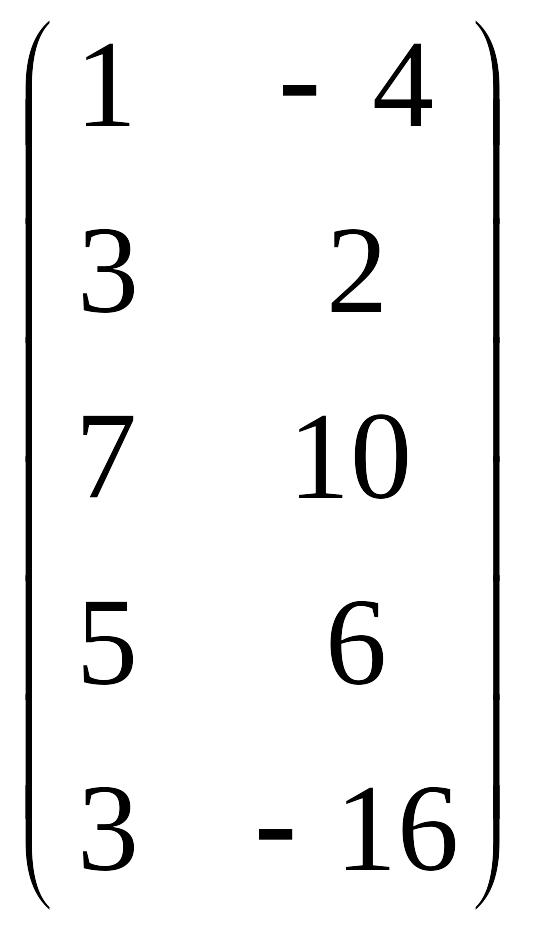2 + 12 = 14
0; RgA
= 2;
A*
=
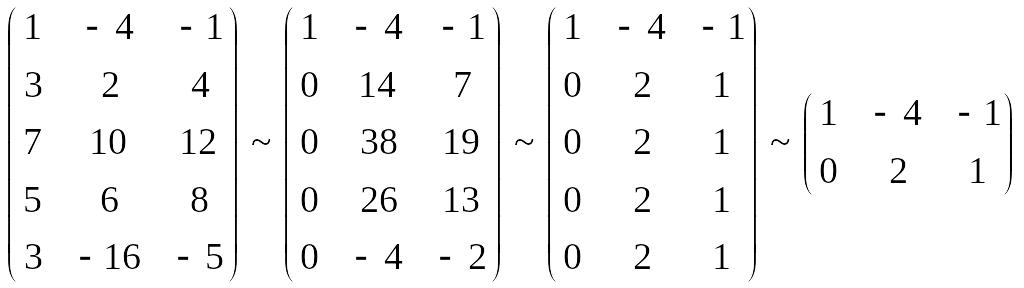
RgA*
= 2.
Система совместна. Решения: x1 = 1; x2 =1/2.