
- •4.Двойной интеграл по области. Множество меры 0.
- •1.Двойной интеграл по прямоугольнику.
- •3.Сумма Дарбу.
- •2.Класс интегрируемых функций.
- •5.Сведение двойного интеграла к повторному.
- •Пример:
- •11. Несобственные двойные интегралы
- •Интеграл по неограниченной области
- •12. Тройной интеграл по параллелепипеду
- •13. Классы интегрируемых функций для тройного интеграла.
- •14. Суммы д`Арбу и их свойства (для тройного интеграла)
- •15. Тройной интеграл по области. Множество меры "0" (кубиками).
- •Линейность
- •16. Сведение тройного интеграла к повторному.
- •18. Параметрическое задание поверхности.
- •19. Длина кривой.
- •20. Площадь поверхности.
- •21. Интегралы по поверхности.
- •22. Формула Стокса. Условия потенциальности векторного поля в пространстве.
- •2. Условия потенциальности векторного поля в пространстве.
- •23. Формула Остроградского
15. Тройной интеграл по области. Множество меры "0" (кубиками).
![]()
![]()

![]() (Включаем
область
(Включаем
область
![]() в параллелограмм
)
в параллелограмм
)
![]()
(![]() -непрерывная,
-непрерывная,
![]() -разрывная)
-разрывная)
Считаем границу -множеством меры «0»
Множество меры «0» ( в пространстве)-это множество, которое мы можем покрыть кубиками с суммарным объемом сколь угодно малым.
Свойства тройного интеграла:
Аддитивность
![]() (
(![]() ,
т.е. мера пересечения множеств
,
т.е. мера пересечения множеств![]() равна
«0»)
равна
«0»)
Тогда:
![]()
Линейность
![]()
![]()
Если
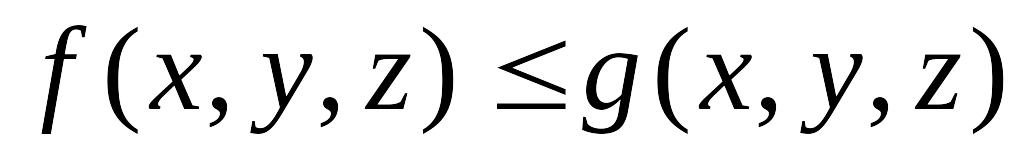 (в
любой точке области
(в
любой точке области
 )
)
![]()
Если известны наименьшее
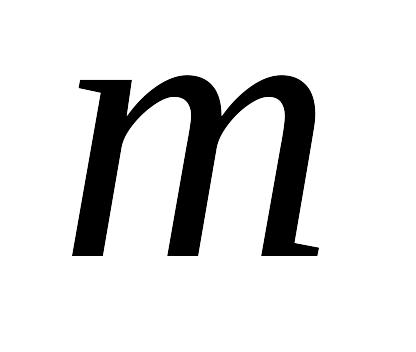 и
наибольшее
и
наибольшее
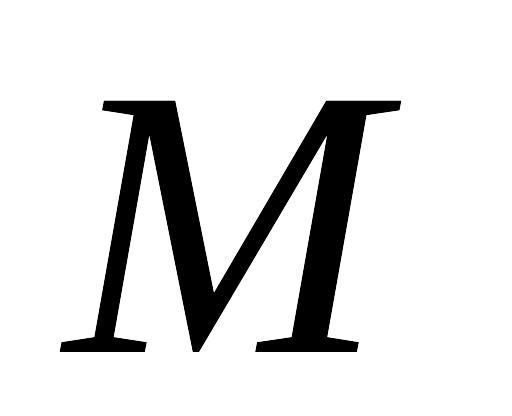 значения
непрерывной функции
в
области
,
то
значения
непрерывной функции
в
области
,
то
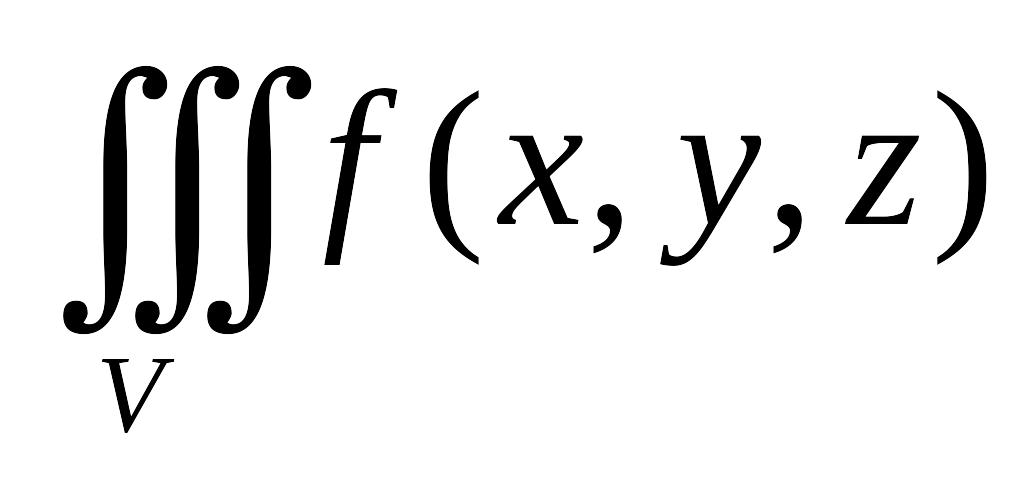 оценивается
так:
оценивается
так:
![]()
Теорема о среднем:
![]() ,
где
,
где
![]() -некая
средняя точка области
-некая
средняя точка области
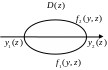
16. Сведение тройного интеграла к повторному.
П



![]()
![]()
![]()
![]() ри
каждом z существует сечение
области
ри
каждом z существует сечение
области
![]() между
между
![]() и
и![]()
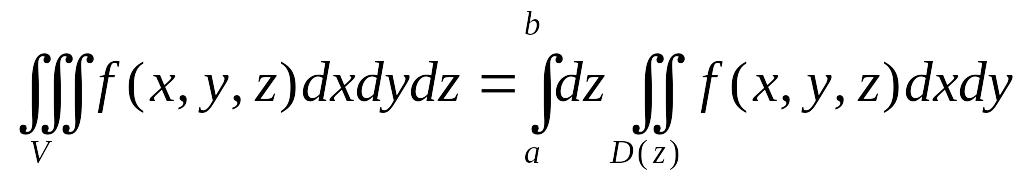 =
=
=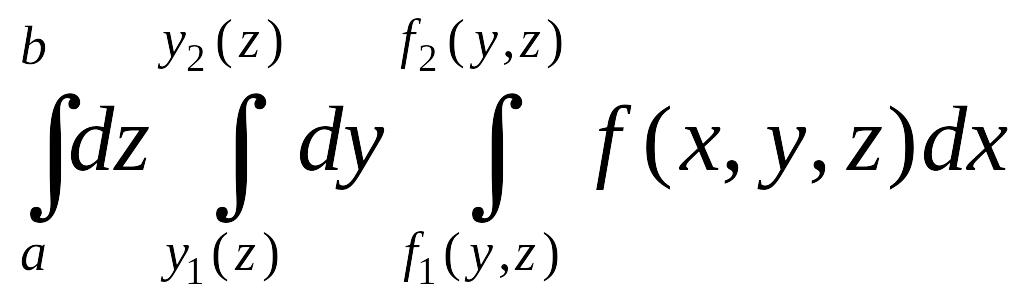
Формула замены переменной в тройном интеграле. Примеры вычисления Якобиана.
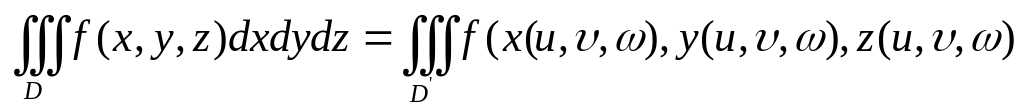
![]()
![]()
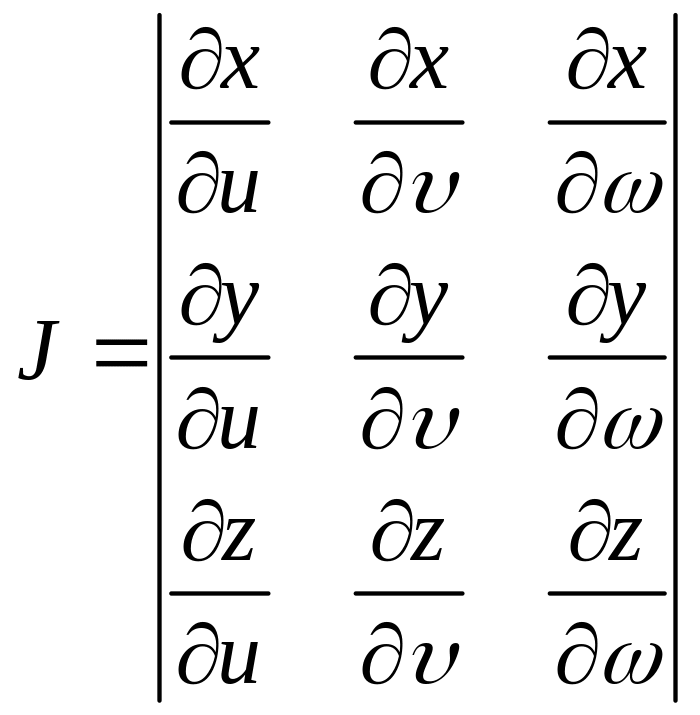 замена
взаимооднозначная.
замена
взаимооднозначная.
Ц илиндрическая
система координат.
илиндрическая
система координат.





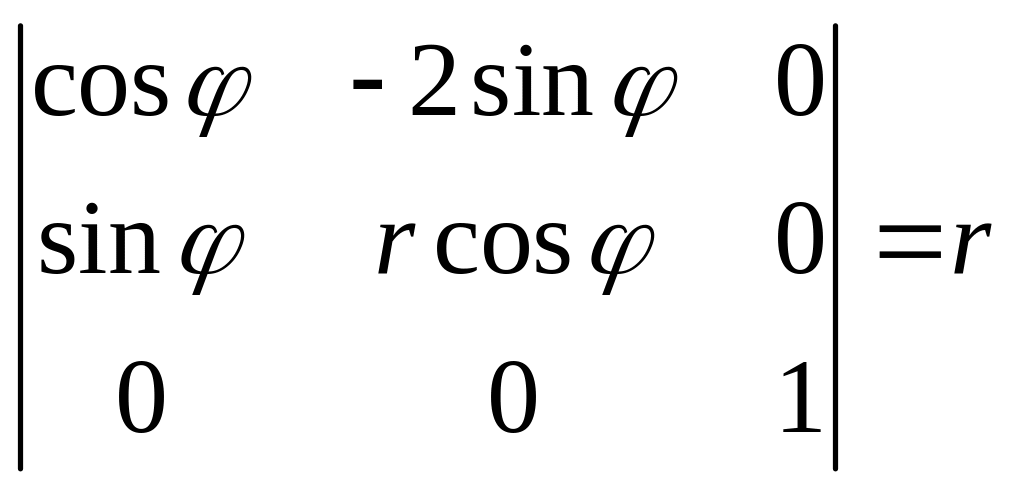

Сферическая система.




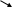

![]()
Экватор
![]()
![]()
![]()
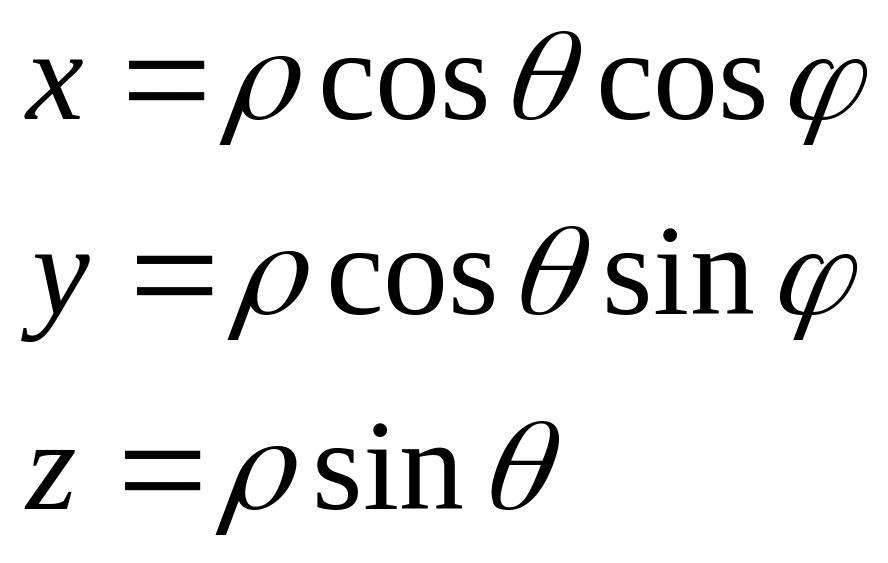
![]()
18. Параметрическое задание поверхности.
Примеры. (цилиндр, сфера)
Способы задания:
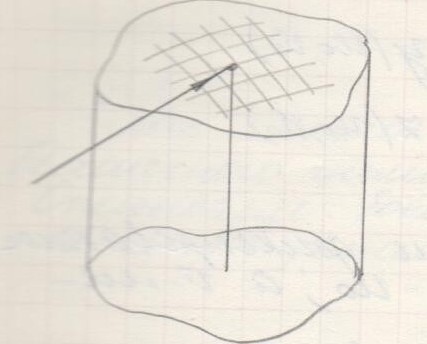 1)
1)
![]() берётся область и задаётся высота точки
берётся область и задаётся высота точки
![]() над плоскостью х. если задана
,
то для каждого х и у задаётся радиус-вектор
над плоскостью х. если задана
,
то для каждого х и у задаётся радиус-вектор
![]() .
.
2)в
неявном виде:
![]()
Например сфера: если хотим представить в первом виде, то надо распилить сферу на две половины и каждую задать.
![]()
![]()
![]()
3)
параметрический способ:
![]() и
и
![]() .
.
Чтобы
задать поверхность, нужно два параметра

![]()
![]() ,
где
,
где
![]()
На
области
задано векторное поле, т.е. задан
радиус-вектор в зависимости от параметров
![]() .
.
Возьмём
точку М
![]() .
Ей соответствуют
.
.
Ей соответствуют
.
Возьмём
фиксированное значение
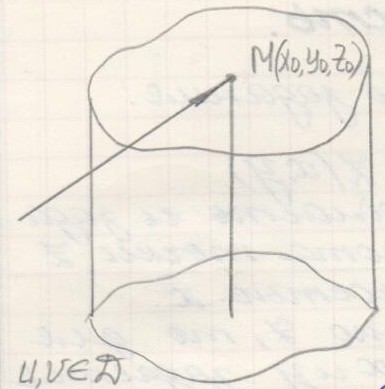
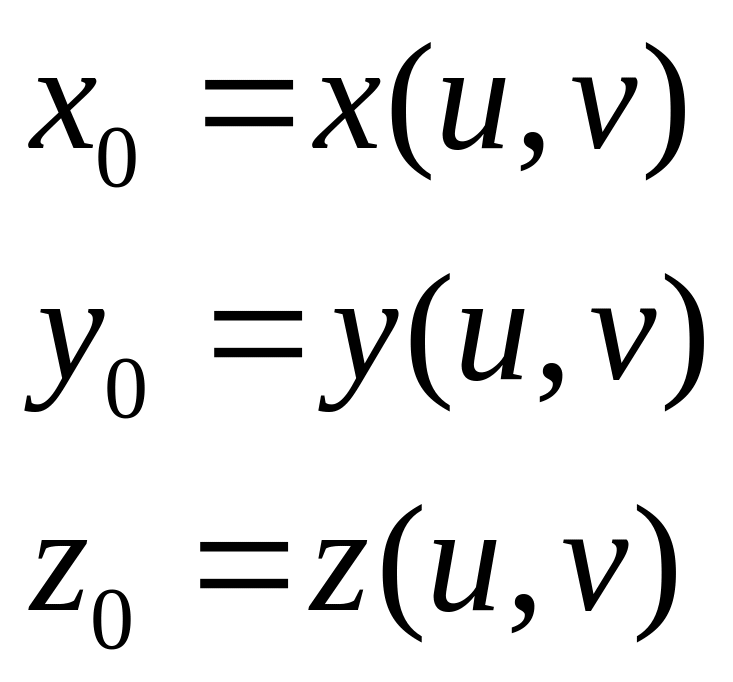
![]() ;
а
;
а
![]() -меняется.
-меняется.![]() - радиус-вектор.
- радиус-вектор.
Мы получили кривую на нашей поверхности.
Теперь
фиксируем
![]() ,
а
будет меняться.
- радиус-вектор.
,
а
будет меняться.
- радиус-вектор.
Получим другую кривую на нашей поверхности.
Взяв другие точки, получим координатную сетку на поверхности. Но здесь мы должны поставить одно условие, координатные линии не должны касаться друг друга.
Система координат невырождена. Взяли вектора вдоль координатных прямых. Эта система векторов будет линейно независима.
Координаты касательного вектора, если смещение вдоль линии .
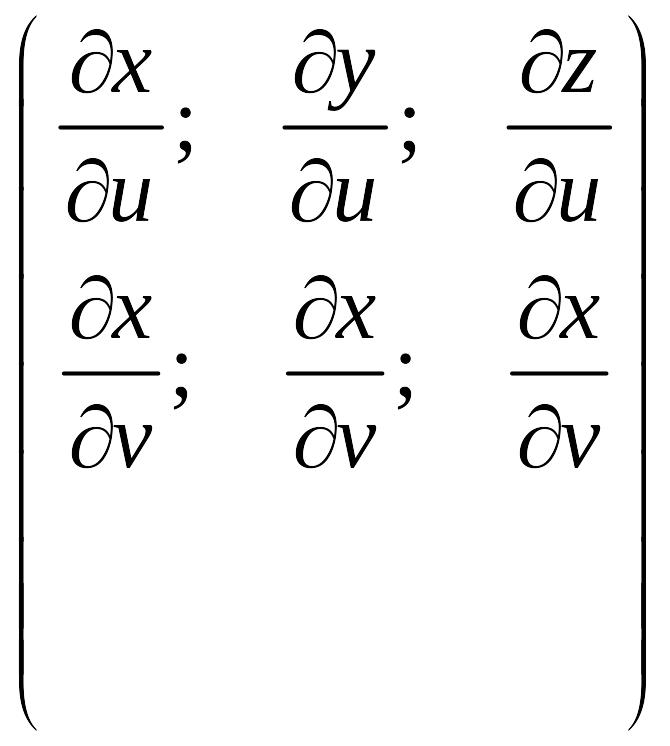 ранг
матрицы равен двум (чтобы эти вектора
были линейно независимые).
ранг
матрицы равен двум (чтобы эти вектора
были линейно независимые).
Эти вектора линейно независимые.
![]() (условие
линейной независимости: векторное
произведение
(условие
линейной независимости: векторное
произведение
![]() )
)
Пример:
Как можно описать поверхность бесконечного цилиндра?
О
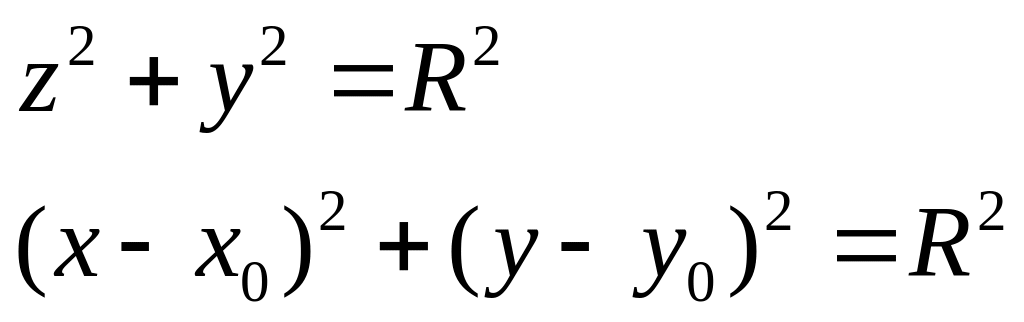
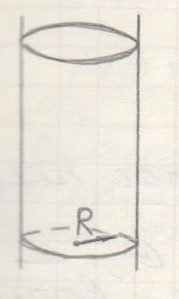
Третий способ задания:
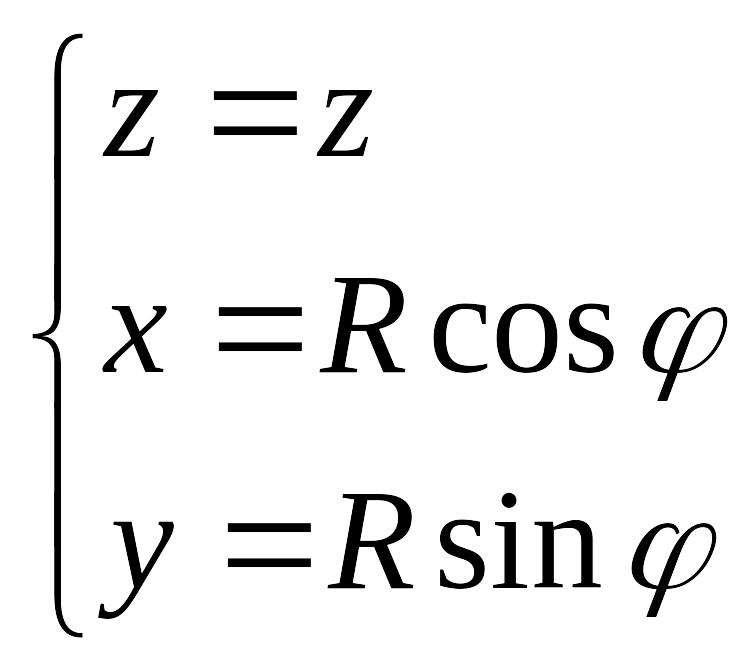 цилиндрический
способ задания.
цилиндрический
способ задания.
Получили
два параметра:
и
![]() ,
примем
-любое,
а
меняется от 0 до
,
примем
-любое,
а
меняется от 0 до
![]() .
Область
представляет собой бесконечную полосу.
.
Область
представляет собой бесконечную полосу.
Радиус –вектор
имеет координаты: Эти
вектора перпендикулярны; первый имеет
длину=1, второй – R.
Если
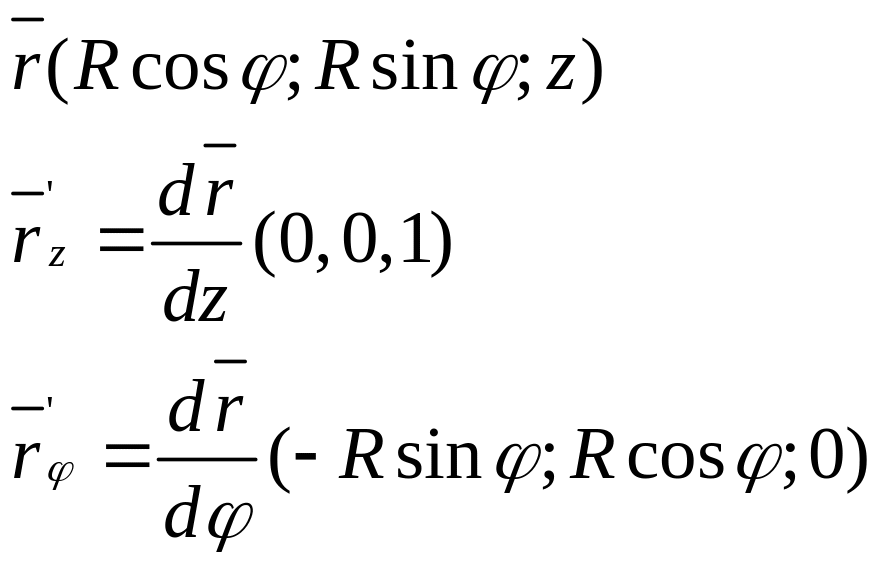
![]() ,
то параметризация невырожденная.
,
то параметризация невырожденная.
Теперь цилиндр:
(радиус R)
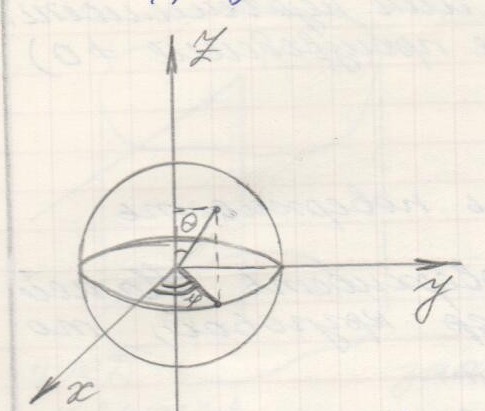 возьмём
возьмём
![]() сферы. Ей мы можем сопоставить два угла:
сферы. Ей мы можем сопоставить два угла:
![]() и
.
Свяжем декартову систему и сферическую.
и
.
Свяжем декартову систему и сферическую.
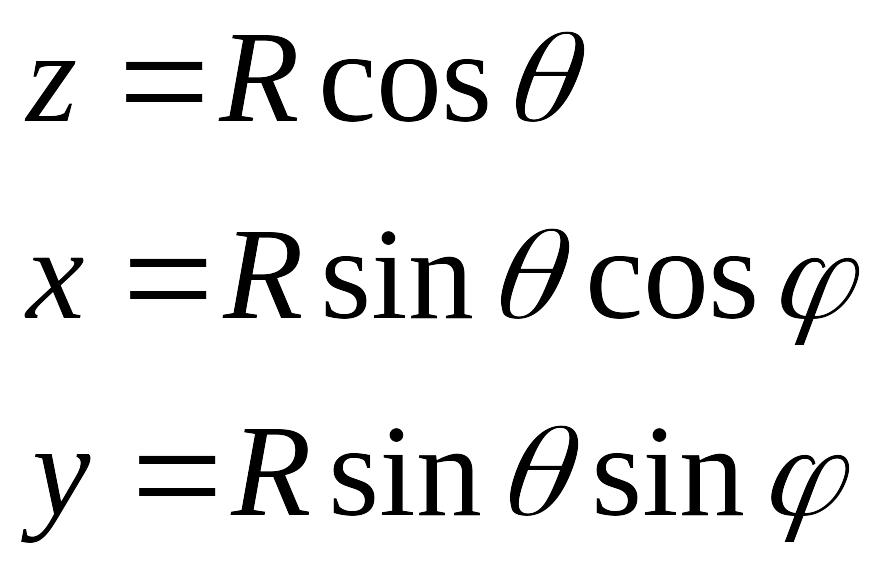
Каким образом совершается переход от одних к другим?
Зная можно вычислить , а зная , а также х и у можно вычислить .
![]()
Будет ли эта система координат вырожденной?
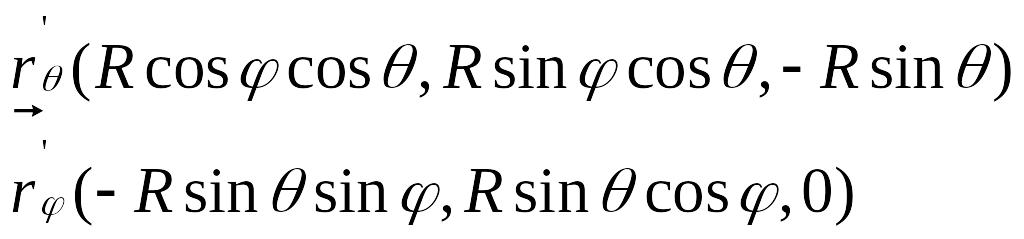
Чтобы узнать, вырождена система или нет, надо посчитать векторное произведение.
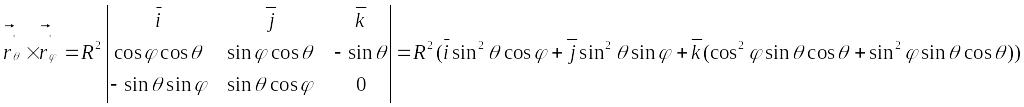
В итоге получим вектор с координатами:
![]()
Если найдём сумму квадратов, то получим единицу.
![]()
![]()
Система
невырождена во всех точках кроме точек,
где
![]() ,
то есть в этих точках система будет
вырождена.
,
то есть в этих точках система будет
вырождена.
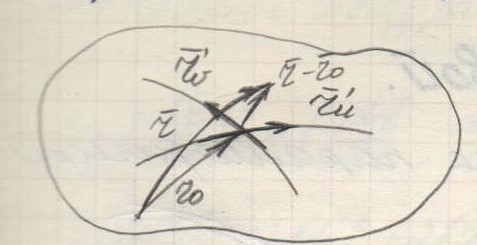
Третий способ задания – параметрический:
![]()
![]() и
и
![]() - это касательные векторы.
- это касательные векторы.
Вектор
нормали – это векторное произведение
этих двух векторов.
![]()
Если мы хотим, чтобы он был единичный, то:
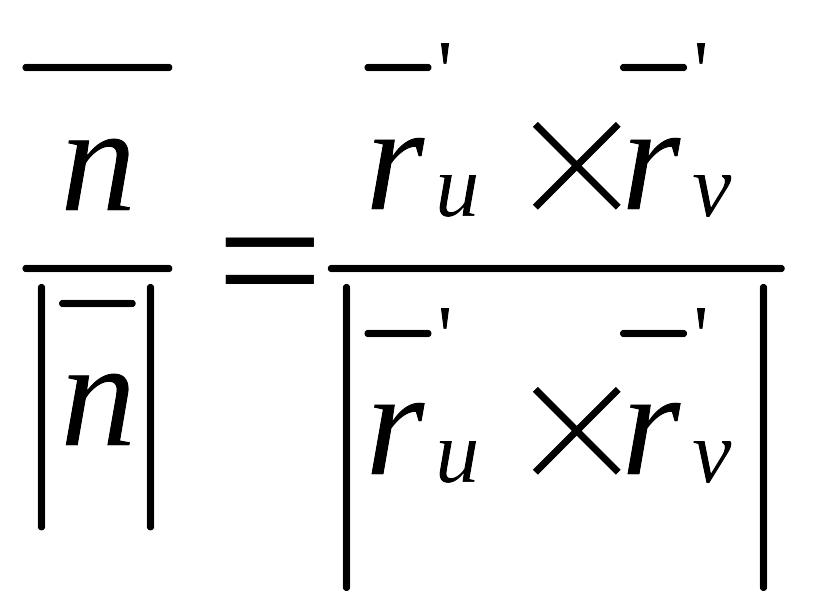
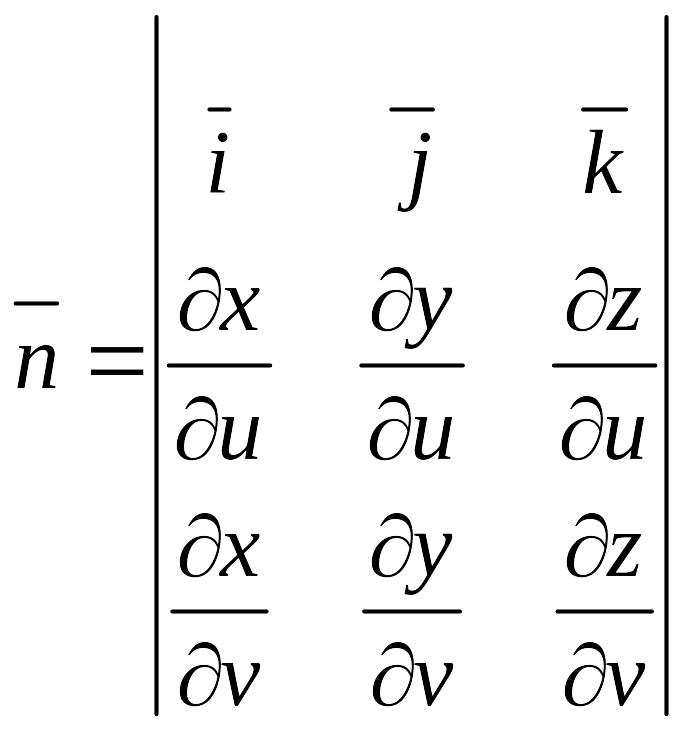 если
уравнение нормали, то надо добавить
если
уравнение нормали, то надо добавить
![]() и
и
![]()
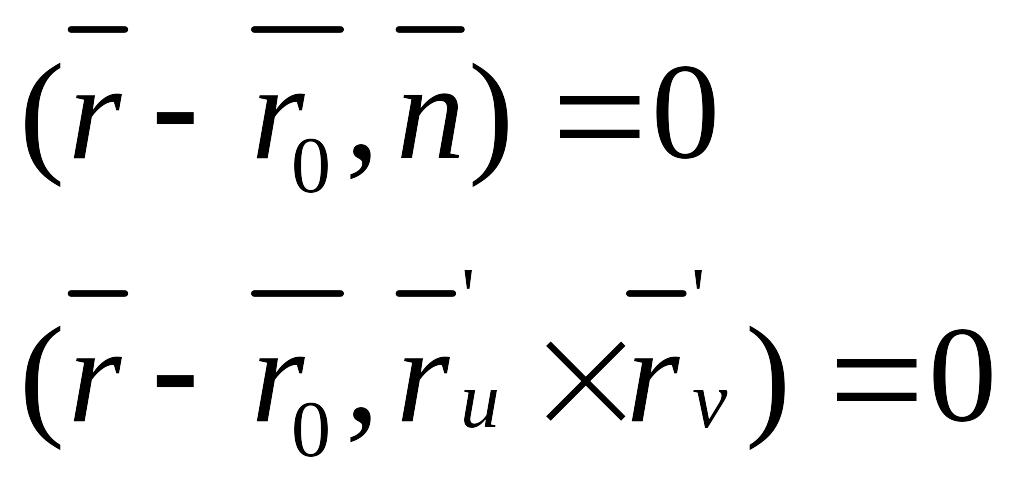 круглые
скобки обозначают скалярное произведение.
круглые
скобки обозначают скалярное произведение.
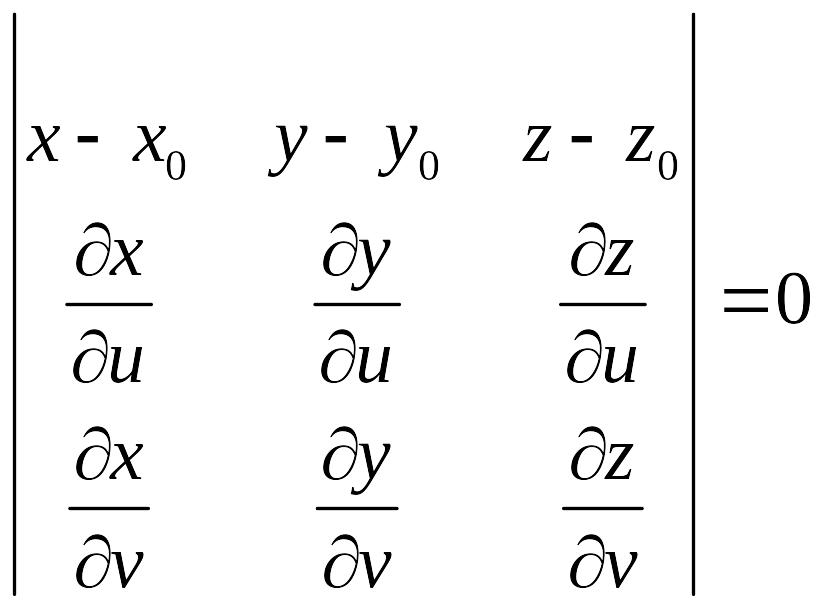
Равенство нулю смешанного произведения обозначает равенство нулю также и определителя.
Нормаль к сфере направлена вдоль радиуса-вектора.
