Интегральное исчисление.

Функция нескольких переменных. Двойной интеграл. Определения. Свойства.

4.Двойной интеграл по области. Множество меры 0.

Есть заданная и непрерывная на [a,b] . Ее можно проинтегрировать:

А если функция двух или трех переменных?

Заданная и непрерывная в области D.

Тогда:

П

D

y

усть у нас есть некая ограниченная область D

x

a

b

c

d

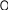
Если она ограничена, то всегда можно получить некоторый прямоугольник. Причем внутри D - , а в кусочках функцию можно определить как равную нулю.

Это произведение множеств

Это обозначение для прямоугольника

1.Двойной интеграл по прямоугольнику.

Определим интеграл для прямоугольника.

Раздробим его на кусочки.

По x – i

По y – j

i и j – номера кусочков

Выберем точку с координатами . Посчитаем значение функции в этой точке.

И так, для каждого кусочка образовали интегральную сумму.

-

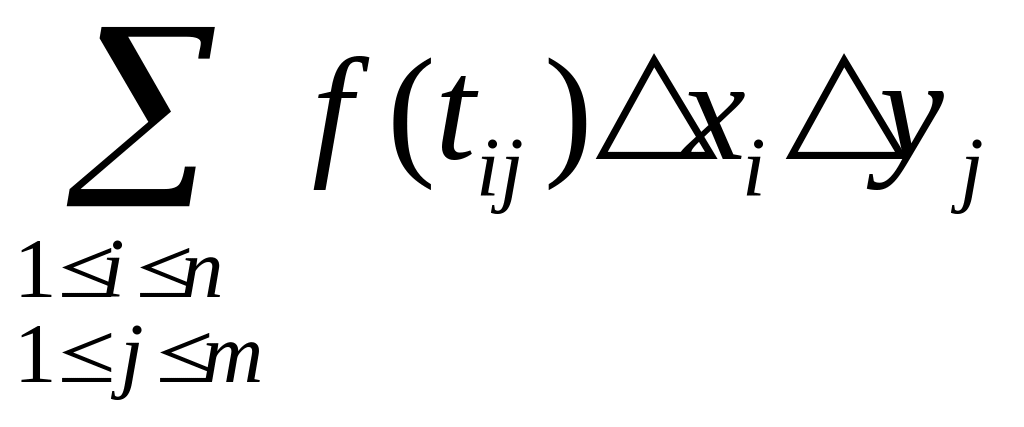
- площадь маленького прямоугольника

Если существует предел от интегральной суммы, когда ранг дробления по каждой переменной :

Если существует такой предел, не зависящий от выбора точек и от способа дробления то, он и будет интегралом:

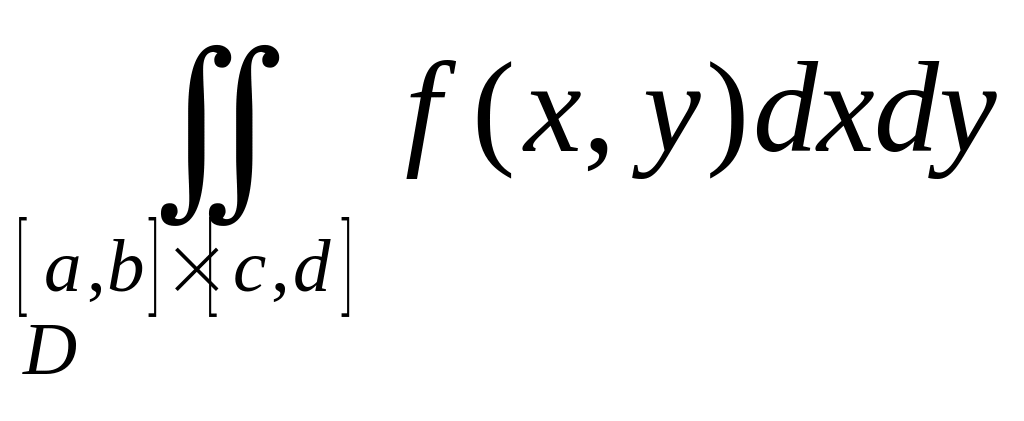
3.Сумма Дарбу.

По аналогии можно определить верхние и нижние суммы Дарбу:

Пусть

Тогда

И тогда наша сумма расположена между этими суммами Дарбу:

Для непрерывных или кусочно-непрерывных функций интеграл существует.

Если функция интегрируема, то сумма Дарбу сходится к интегралу:

Свойства интеграла.

1.Аддетивность

Если

(эти множества не пересекаются)

Оно доказывается элементарно:

В интегральном примере будут точки, попадающие в и

В опрос только в том, что в некоторые кусочки могут попасть кусочки как , так и

Если функция интегрируема, то она должна быть ограничена. А если так , то эти кусочки, их общая площадь . И останется только интеграл по и интеграл по .

2. Линейность

а.

б.

Интеграл от суммы = сумме интегралов

3.

Если это справедливо, тогда справедливо следующее:

4. Если - интегрируемы, то произведение тоже интегрируемо

5.

Следует из свойства модуля, примененных к интегральным суммам.

Если функция интегрируема, то и ее модуль будет интегрируем.

6. Аналогично теорема о среднем.

Если ,

В частном случае, когда , мы получаем:

2.Класс интегрируемых функций.

1.Непрерывные функции на интегрируемы.

Доказательство:

По теореме Кантора функция равномерно непрерывна , если она замкнуто-ограничена

колебание функции

2. Всякая ограничено-непрерывная функция на D , за исключением конечного числа линий принадлежащих это области , интегрируема по этой области.

Д оказательство:

с

Q

D

D-Q - замкнутая область

Q- открытая область

Разбиваем область

Тогда, =Q, а остальные лежат вне Q

Мера Жордана.

Есть некое множество – D.

Включим в него некий прямоугольник

Характеристическую функцию множества определим следующим образом:

{

И тогда под площадью множества M(D) понимается интеграл:

5.Сведение двойного интеграла к повторному.

Это способ реально посчитать интеграл.

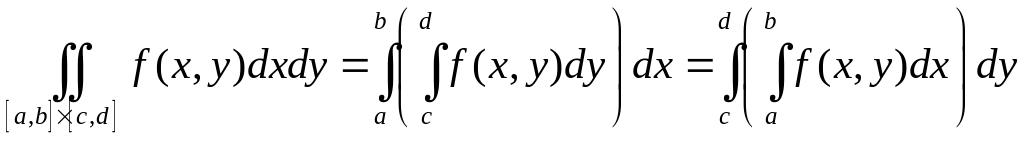
Доказательство.

Опишем сначала для прямоугольника.

Пусть у нас функция интегрируема.

Введем обозначения:

Раздробим область.

Для всех точек имеем: (если x,y из соответствующего элементарного прямоугольника с номером i,j)

Теперь интегрируем это непрерывно по y в пределах маленького элементарного прямоугольника.

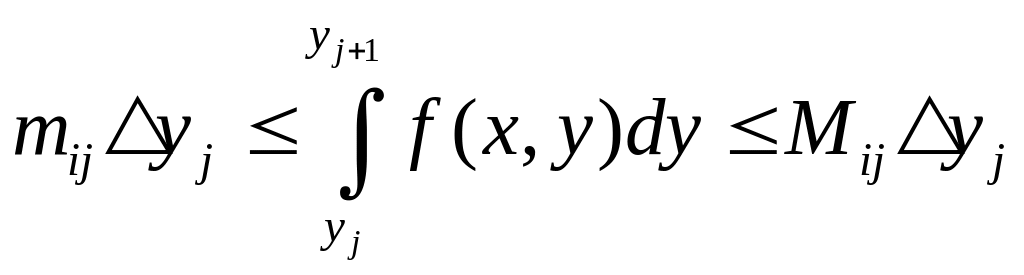
Просуммируем по всем прямоугольникам. Суммируем по вертикальной полосе (i).

i

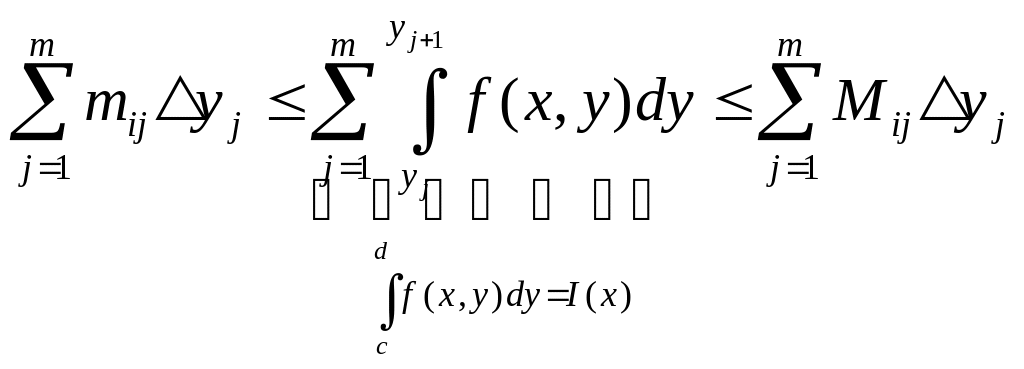
Теперь домножим на и проинтегрируем по i от 1 до n:

Когда ранг дробления , то

А интегрируем сумма , ну а это равно двойному интегралу:

Формула доказана.

Теперь если область не прямоугольник.

Предположим сначала, что это криволинейная трапеция, которая задается двумя функциями .

В

зяли фиксированное x

D

a x

b

Включим эту трапецию в прямоугольник и применим формулу:

Основная формула для вычисления двойных интегралов.

С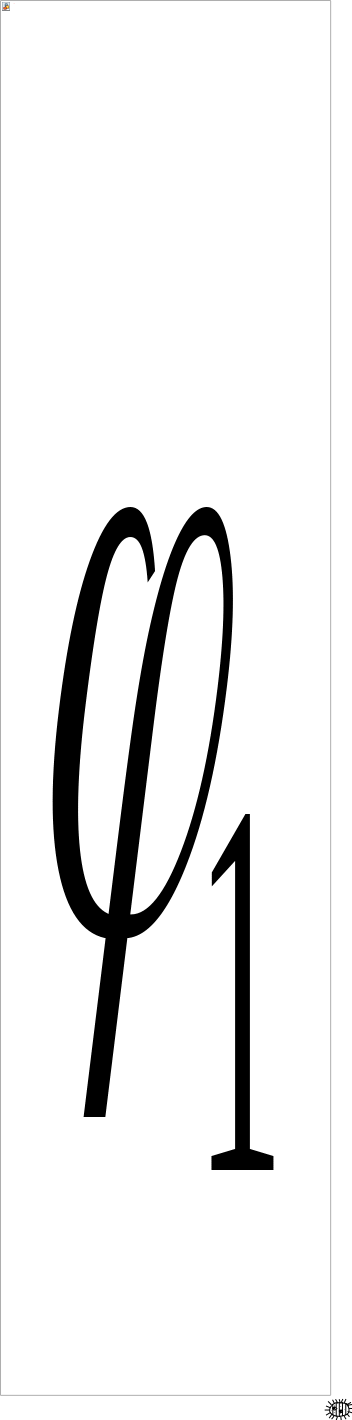 лучай сложной области.

Разбиваем эту сложную область на элементарные.

1

2

3

4

5

6

7

9

8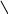

Если интегрируем сначала по х, то можно разбить так

Криволинейный интеграл первого рода.

З адана некая кривая (рассмотрим случай плоскости).

В каждой точке кривой задана функция .

Тогда можем ввести криволинейный интеграл первого рода.

Параметр S - параметр длины кривой (длина в текущей точке).

, где - длина кривой. (не важно из какой точки мы движемся: из А или из В)

В случае пространства:

Однако , обычно мы имеем параметрически заданную прямую:

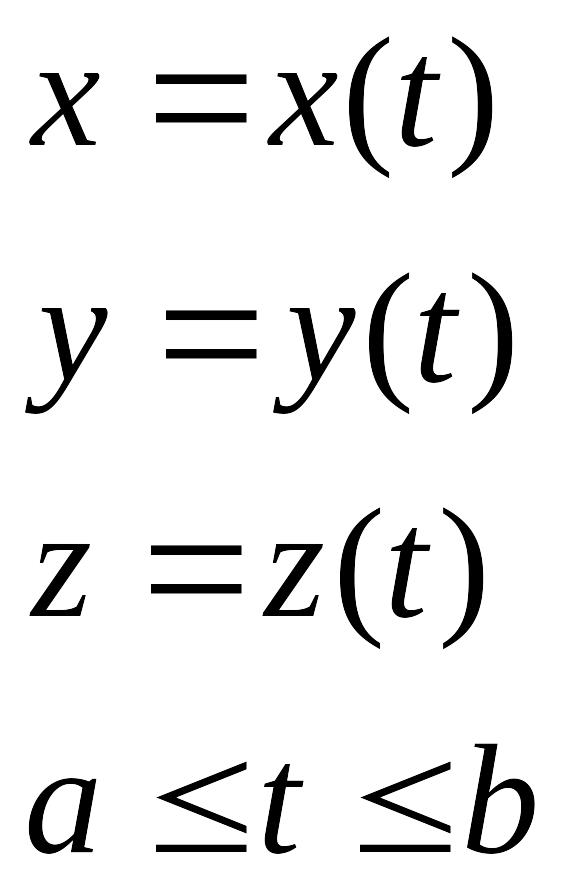
Тогда интеграл выглядит:

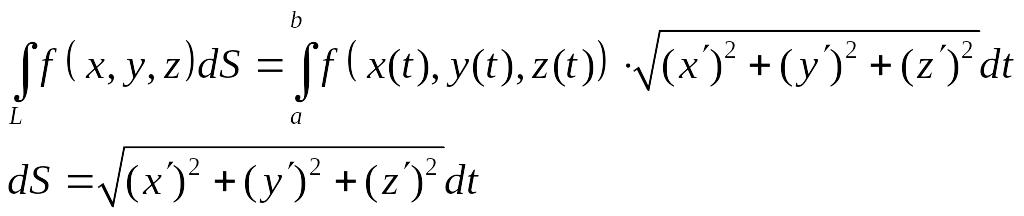
Т.е. таким образом мы разбиваем кривую на кусочки.

Н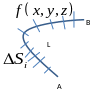 а -том кусочке (длина дуги длине участка ломаной)

Этот корень можно записать как:

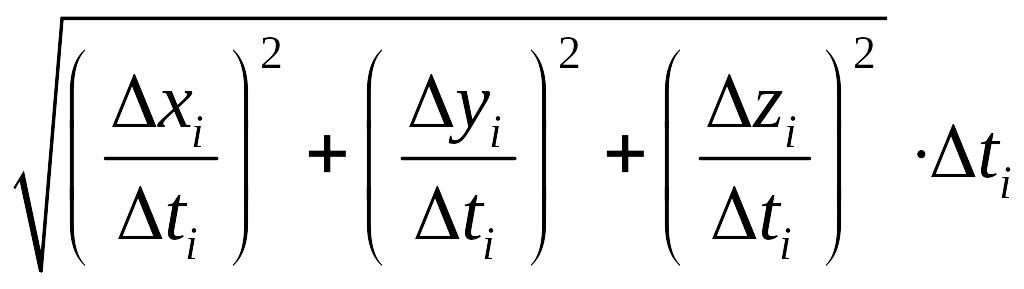
В пределе это устремится к соответствующим производным.

Криволинейные интегралы второго рода.

Е сть кривая L в пространстве выбрали на ней определенное направления. Тогда можно определить такой криволиней интеграл второго рода:

где - функции, заданые на нашей кривой. Будем считать их непрерывными или кусочно-непрерывными

-параметр кривой: (оно пробегает такие значения)

Параметризация такова, что пробегается наша кривая.

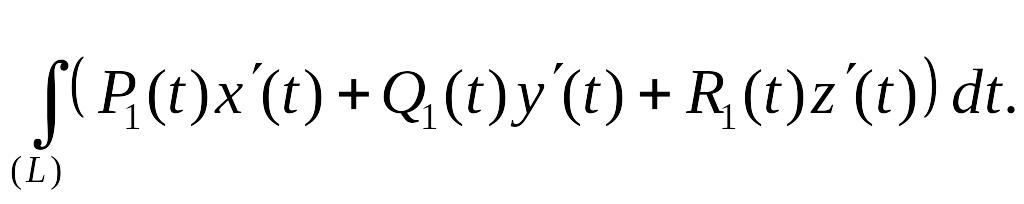
Делай замену:

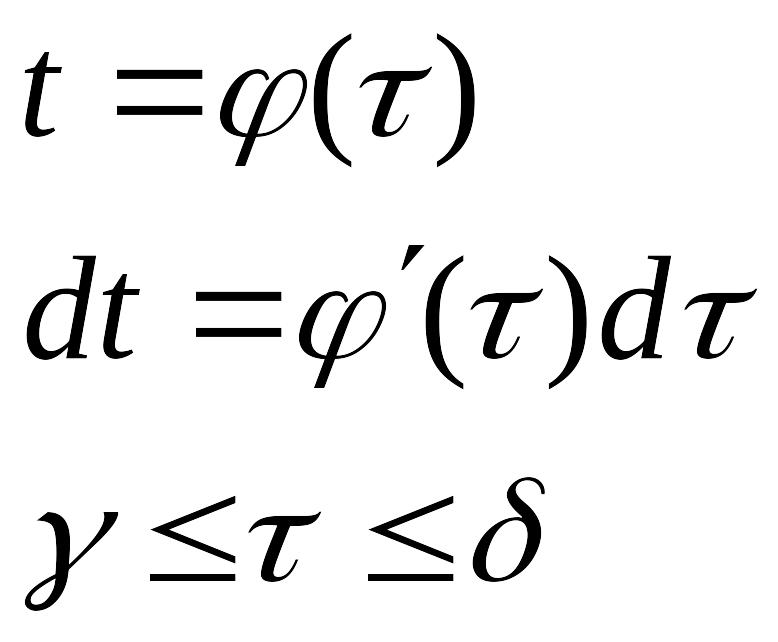
Тогда наш интеграл примет вид:

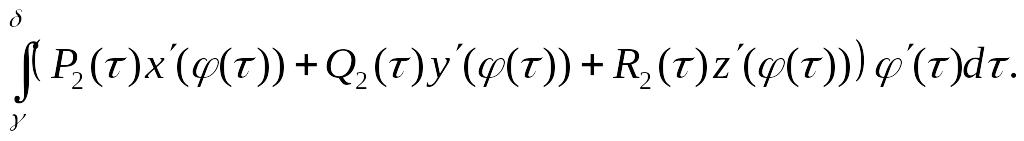
Интеграл не зависит от того, каким образом мы параметризовали кривую.

Есть некоторая область в трехмерном пространстве (частный случай – на плоскоти). В каждой точке заданы три функции (или - на плоскости)

Мы можем считать, что в каждой точке задан некоторый вектор с координатами

Говорят, что задано векторное поле, когда в каждой точке области задан некоторый вектор.

П усть в нашей области задана некоторая кривая

Возникает вопрос, когда этот интеграл зависит от начальной и конечной точек, а когда от того по какой кривой мы интегрируем?

Если интеграл – функция от начальной и конечной точек, то мы можем определить потециал

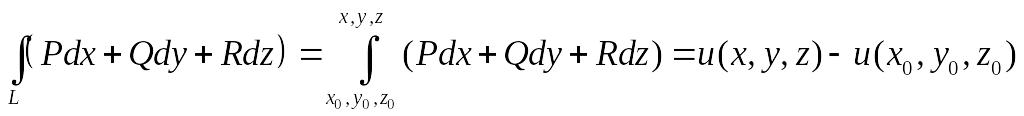
Интеграл не зависит от пути интегрирования.

(знак «-» от того, что кривая пробегается в обратном направлении. И в параметризации:

Потенциал – это многомерный аналог неопределенного интеграла. Это некий аналог первообразной. Он определен с точностью до постоянного слогаемого.

Когда интеграл не зависит от пути интегрирования?

К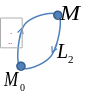 ритерий потенциальности векторного поля.

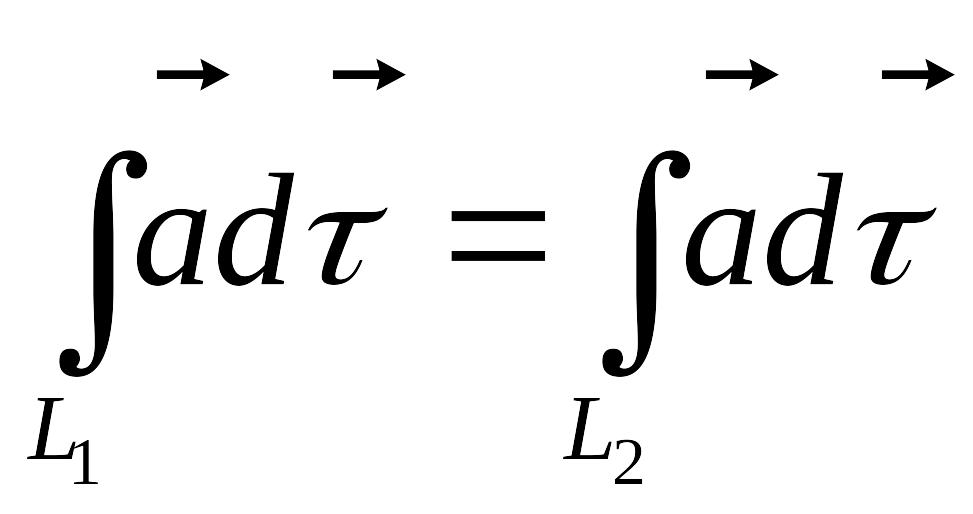(*) – это выполняется тогда, и только тогда, когда:

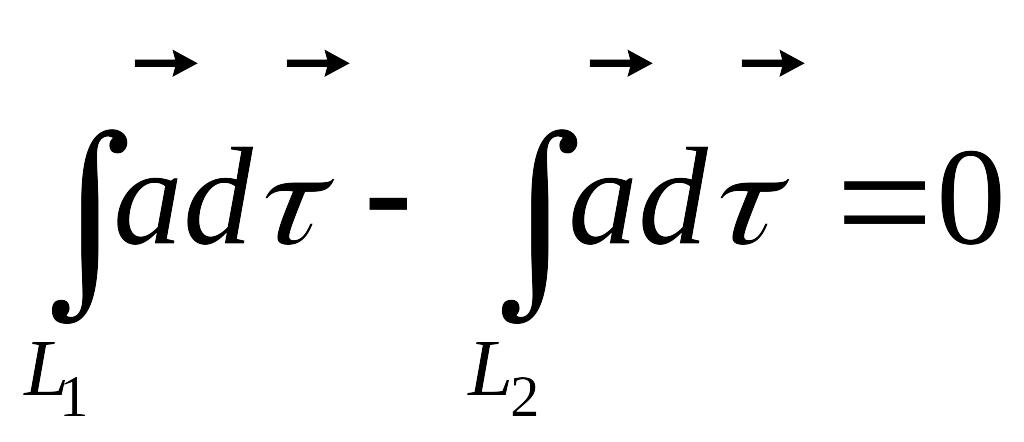или 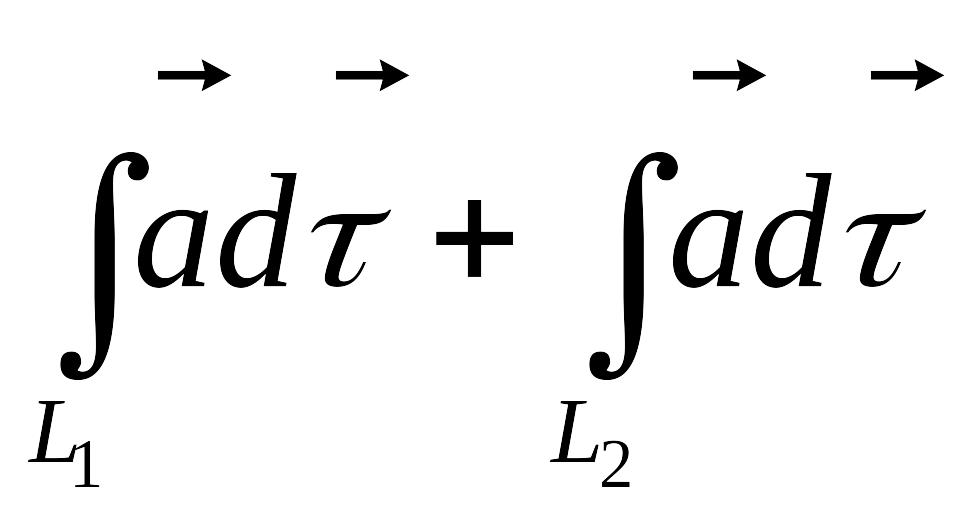= Знак «-» внизу интеграла указывает на то, что интегрируем в обратном направлении

- контур. Мы движемся сначала по , а потом по , но в обратном направлении

=

Интеграл по кругу равен нулю. Для того, чтобы интеграл был независимым от пути интегрирования, надо чтобы интеграл по замкнутому контуру был равен 0.

Если выполняется равество (*), то интеграл по замкнутому кругу = 0.

Полу потенциально тогда, и только тогда, когда:

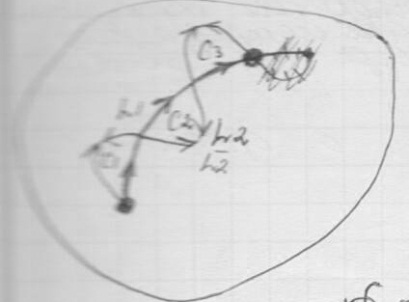По - стрелки в обратную сторону.

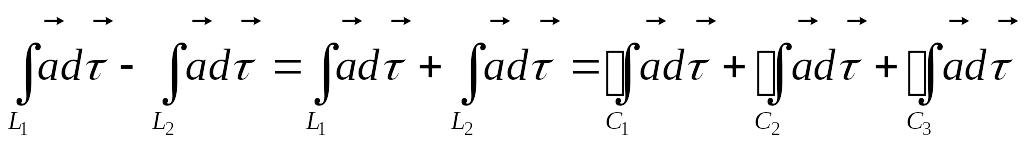
Выразим через потенциал

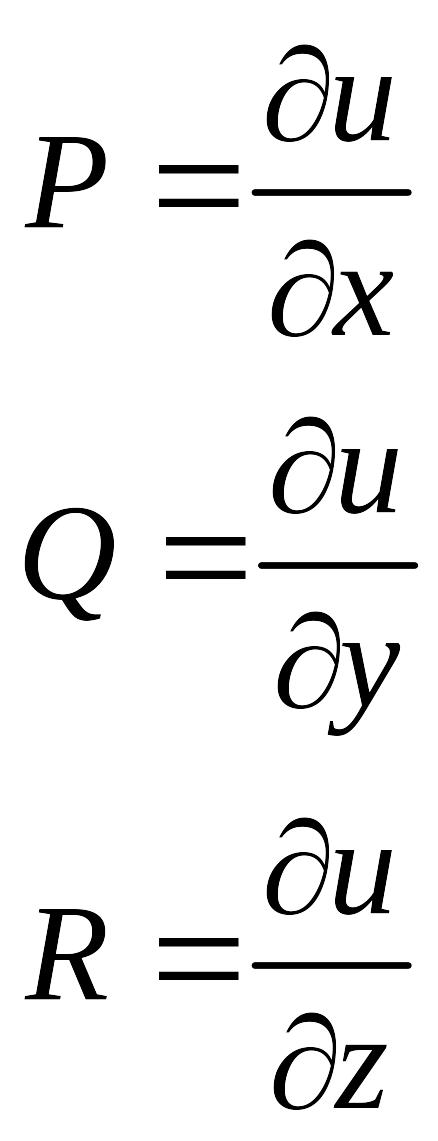- некоторые непрерывные функции.

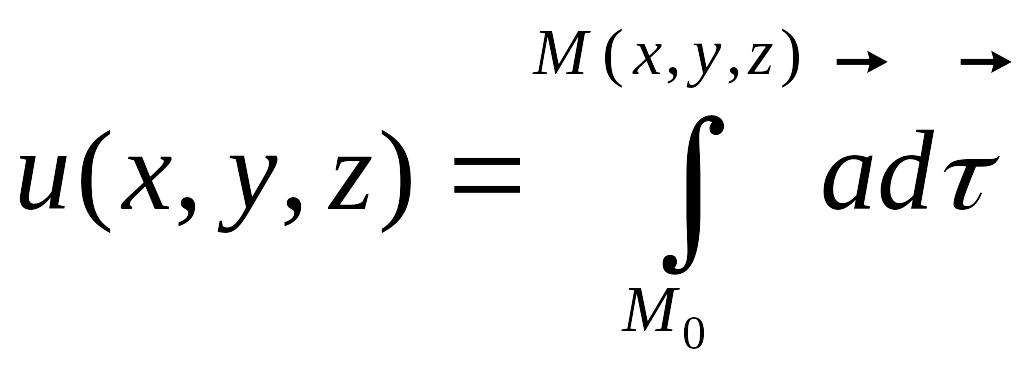
Выполним приращение:

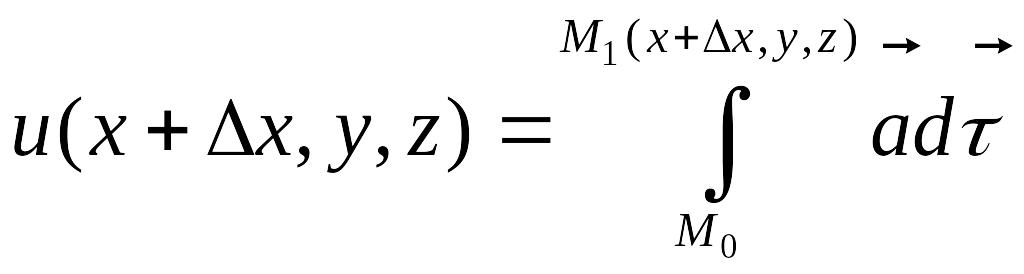
Если приращение достаточно маленькое, а область достаточно хорошая, то точка M₁ достаточно близка к точке М и можно провести прямолинейный отрезок. Он тоже будет находиться в области точки М.

Тогда разница:

= Но по этому пути и и

= == выбрали такую параметризацию когда

Воспользуемся теоремой о среднем:

==

В силу непрерывности функции

Зачит (остальные случаи доказываются аналогично)

Предположим, что - непрерывно дифференцируемые функции. Тогда:

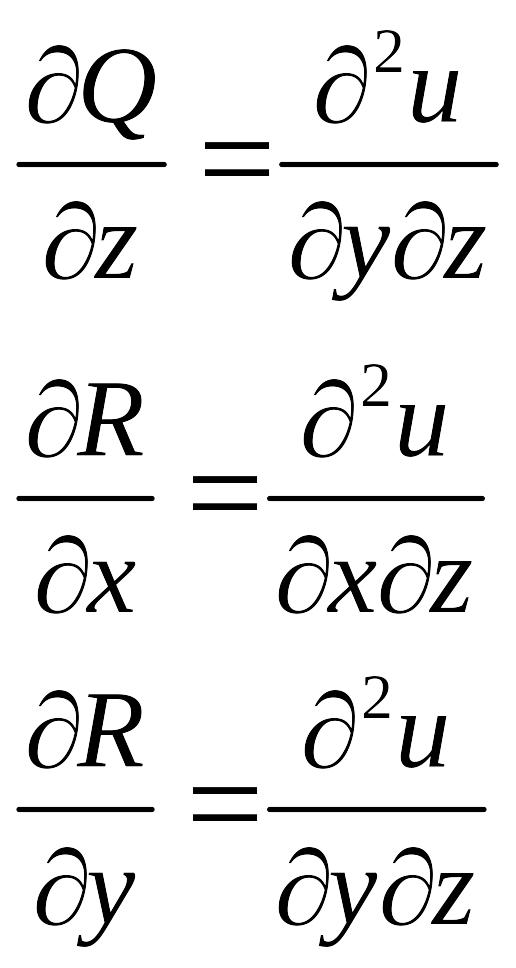
Тогда:

Это необходимое условие потенциальности.

Сначала докажем плоский случай ( нет ) ,

Для этого сначла выведем формулу Грина.

Формула Грина.

, где - так обозначается граница области D.

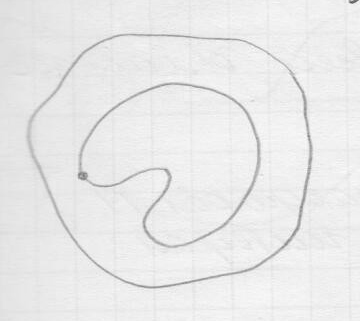
Если интеграл по внешнему контуру равен нулю, то равен нулю интеграл и по некоторому внутреннему контуру.

Формула Грина.

Сначало вывод для следующей области:

С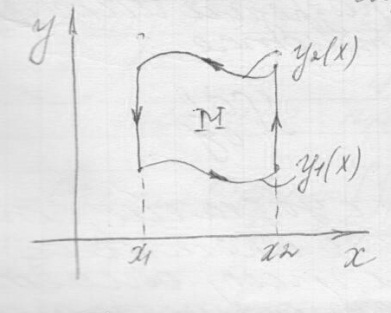 водим двойной интеграл к повторному :

= ==

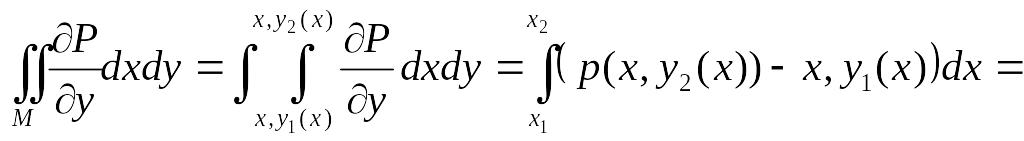
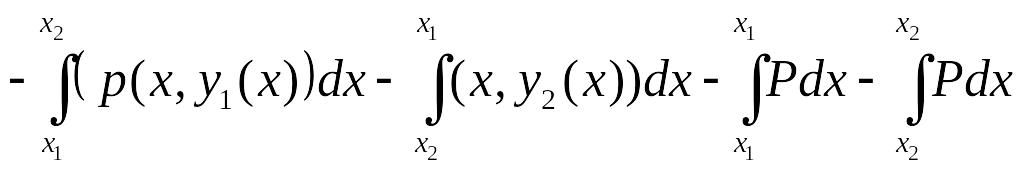делаем замены чтобы обходить область всё время в положительном направлении.

Последние два интеграла равны нулю, т.к. не меняется.

== - вдоль всей области

Если для взять такую область М, то так же получим интеграл:

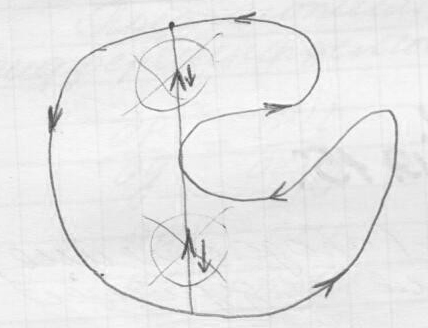
Эту область можно разбить на элементарные .

Провели вертикальную черту. Получили три кусочка.

По внутренним разрезам интегралы взаимно уничтожаются.

Если область с дырами, то дырка обходится в обратном направлении так, чтобы область находилась слева. Делается необходимые разрезы.

Что касается , то это делается следующим образом – область ограничивается горизонтальными линиями.

В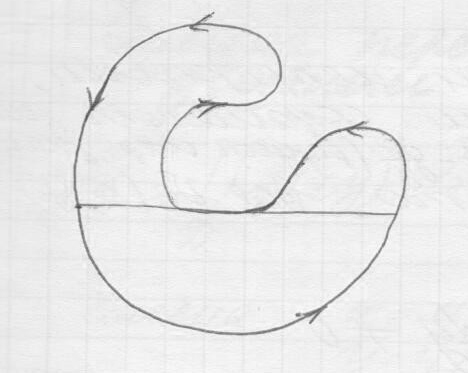 нутренние интегралы также сокращаются.

В результате сложения получается формула Грина.

Необходимое и достаточное условие потенциальности поля.

Есть векторное поле.

Вектора с координатами

Необходимое и достаточное условие:

Обращение в ноль интеграла по любому замкнутому контуру С.

П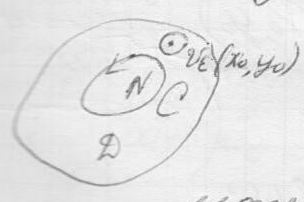 усть область D

Односвязная и поле непрерывно дифференцируемое. Тогда можно применить формулу Грина.

Если везде в области

Значит везде в области интеграл = 0

Следовательно поле будет поленциально.

Теперь наоборот.

Псть в некоторой точке область

Т.к. эти функции непрерывны, то в некоторой области они сохраняют знак (разность сохраняет знак)

Предлагаем, что вся лежит в области.

Тогда

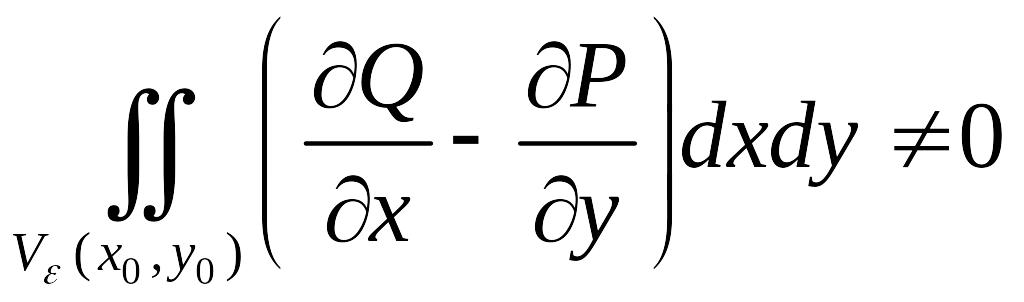
Т.к.

(не только сохраняет знак, но и больше некоторого )

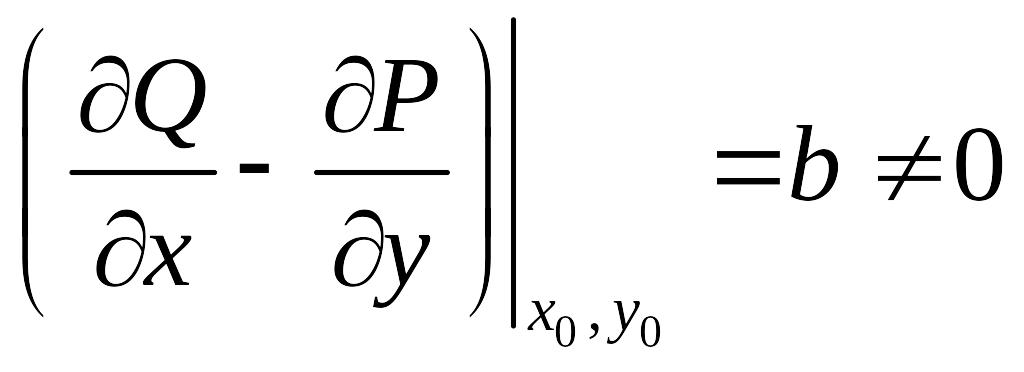в точке

в она может доходить до

Тогда

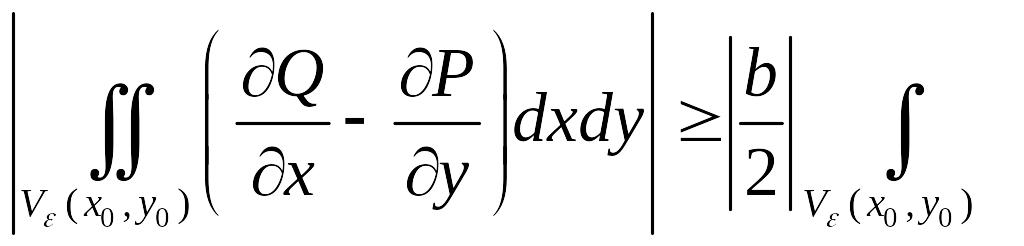
Т.е. это не ноль. Значит интеграл по границе не ноль, т.е. поле не будет потенциальным.

- необходимое и достаточное условие.

Замена переменных в двойном интеграле.

Дано:

Замена:

Выведем аналогичную формулу для двойного интеграла.

Замену будем считать взаимно однозначной.

В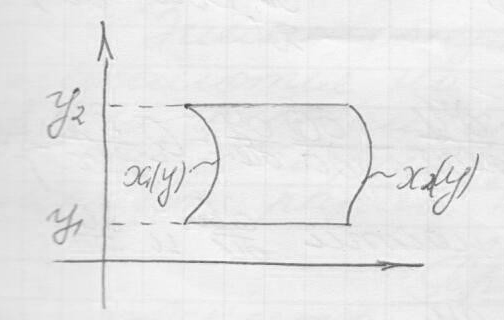 ыбираем область, а также функцию

выберем некоторую функцию , которая

Тогда - такая функция:

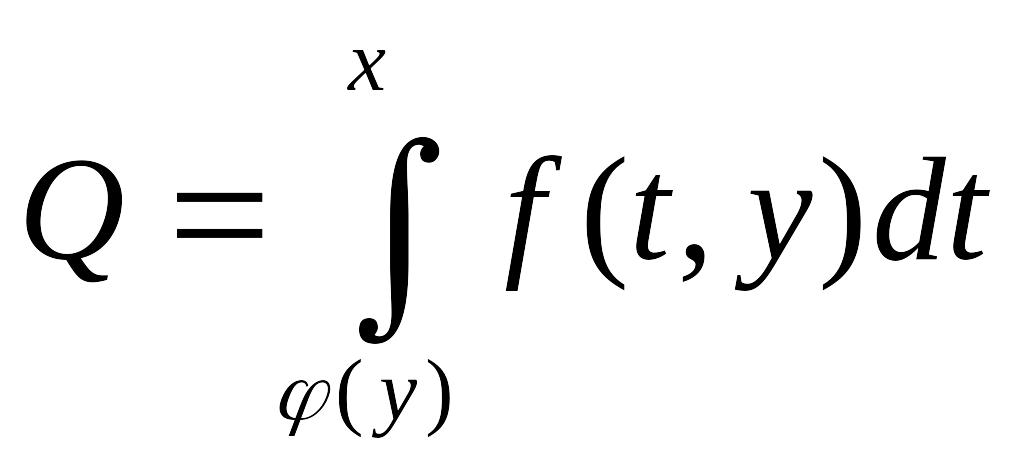
Тогда производная интеграла по верхнему пределу будет

Следовательно:

Это частный случай формулы Грина, в котором P=0

В последнем одномерном интеграле можно сделать замену переменной.

=

Теперь сгруппируем:

= [применим формулу Грина, и предположим, - дважды дифференцируемые функции]

= ==

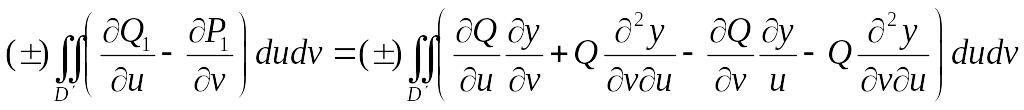Найдем и

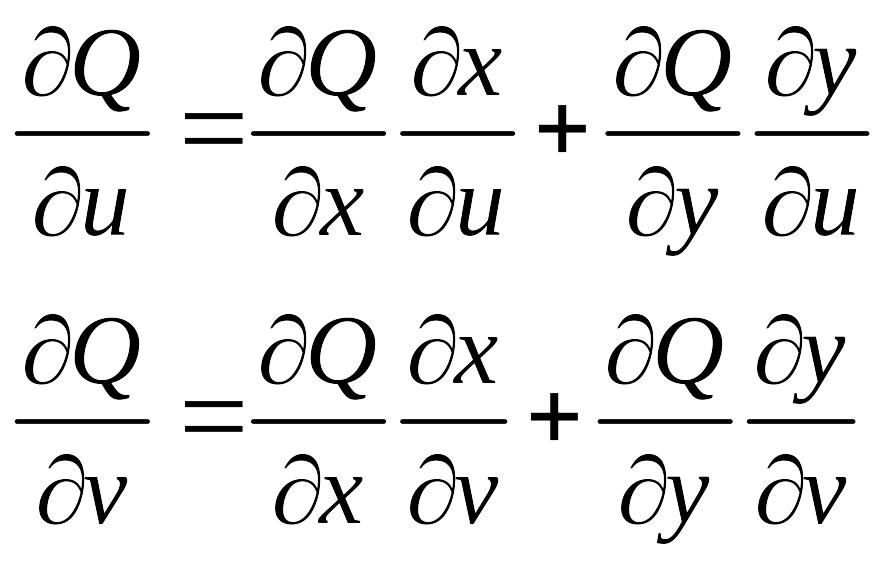подставим эти выражения в интеграл.

== =

===

- якобиан. Это определитель матрицы.

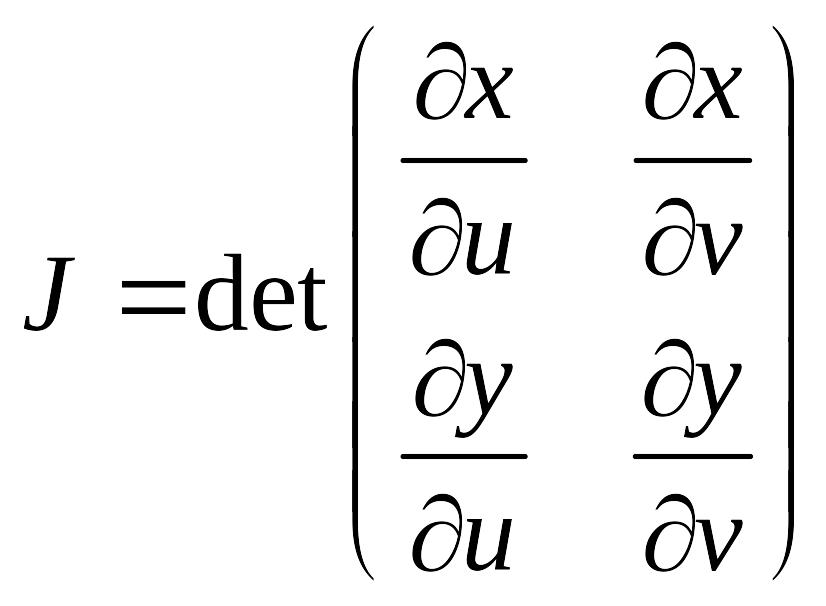это матрица дифференцированная от замены переменных.

Разберемся теперь со знаком. Знак не должен зависить от того, какая у нас функция, а только от замены переменной.

Если функция положительная, а якобиан отрицательный, то знак «-», если якобиан положительный, то знак «+».

===

Знаки обхода соответсвтвия контуров меняются на противоположные, если якобиан отрицательным.

Формуле верна же для области, которую можно разбить на элементарные.