12.5. Обчислення потрійних інтегралів

12.5.1. Основні поняття

Нехай V деяка просторова область, що обмежена замкненою поверхнею S. Область V називають правильною за напрямом осі Оz, якщо вона має властивості:

1. будь-яка пряма, що паралельна осі Оz, перетинає поверхню S не більше ніж в двох точках;

2. уся область V проектується на площину хОу в правильну двовимірну область D.

Аналогічно визначаються правильні тривимірні області за напрямами осей Ох та Оу.

Область V, яка правильна за напрямами усіх трьох координатних осей, називають правильною.

Правильними тривимірними областями є еліпсоїди, піраміди, призми та інші тіла.

Якщо тривимірна область V правильна, то обмежуючу її поверхню S можна розбити на дві частини: нижню – S₁, рівняння якої , та верхню S₂, рівняння якої (див. мал. 6).

z x y 0 a b B A M(x,y,z) N(x,y)

Обидві ці поверхні (отже, і сама область V) проектуються на площину хОу в правильну область D, межа якої точками А та В поділяється на дві криві з рівняннями , .

Позначимо довільну точку області V через М(х, у, z), а її проекцію на площину хОу – N(х, у, 0).

При фіксованих х та у апліката z точки М, що знаходиться всередині області V, може змінюватись від до .

Якщо точка М пересувається всередині області V, то точка N пересувається всередині області D, а її координати (а тому і координати х, у точки М) повинні задовольняти нерівностям .

Отже, координати будь-якої точки повинні задовольняти систему нерівностей

Системи (1) та (2) є аналітичним описом просторової області V.

Якщо функції та неперервні в замкненій області D площини хОу і область V описується системою виду (1), то обчислення потрійного інтеграла можна здійснити шляхом послідовного обчислення інтегралів меншої кратності за формулою:

Якщо область V описується системою вигляд (2), то потрійний інтеграл обчислюють за формулою:

Ці формули найчастіше записують у вигляді:

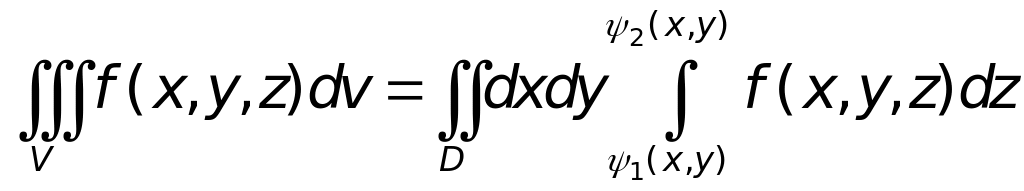(3)

, (4)

відповідно.

Отже, аналітичний опис області V виду (2) дозволяє обчислення потрійного інтеграла звести до обчислення трикратного інтеграла, в якому: межі зовнішнього інтеграла – сталі; межі середнього інтеграла можуть залежати лише від змінної інтегрування зовнішнього інтеграла; межі внутрішнього інтеграла можуть залежати від змінних інтегрування середнього та зовнішнього інтегралів.

Для обчислення потрійного інтеграла в прямокутних координатах крім формул (3) та (4) часто використовують ще формули:

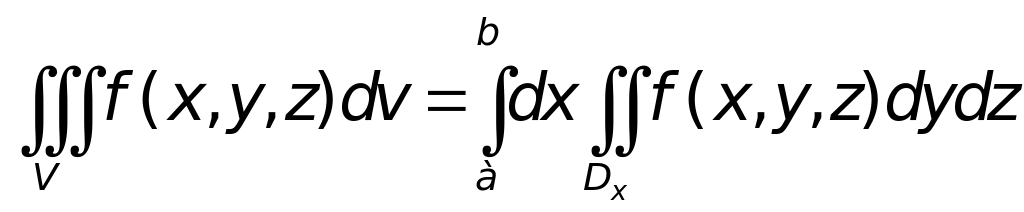(5)

(6)

, (7)

де D_x(D_z, D_у) – перетин області V площиною, яка паралельна площині уОz (площинам хОу та хОz, відповідно) і проходить через довільну точку інтервалу (а, b) (інтервалу (с, d) та ( , q), відповідно) – інтервалу зовнішнього інтеграла.

Ці формули часто спрощують обчислення потрійних інтегралів.

Приклад 6. Обчислити , де область V обмежена поверхнею обертання кривої навколо осі Оz і площиною z = h (h > 0).

Розв’язування. Щоб одержати рівняння поверхні обертання заданої лінії навколо осі Оz, залишимо змінну z в рівнянні лінії без зміни, а у замінимо на . Одержимо: – рівняння параболоїда обертання.

Проекцією області V на площину хОу буде круг х² + у² = h.

Заданий потрійний інтеграл можна обчислити за різними формулами.

Для застосування формули (4) використовуємо аналітичний опис області інтегрування V:

.

Тоді одержимо:

Обчислення інтеграла за цією формулою приводить до громіздких викладок.

Тому застосуємо формулу (6):

,

де D_z є перетин області V площиною, яка перпендикулярна до осі Оz і лежить на висоті z, причому .

Перетин D_z буде кругом радіусом , що випливає із рівняння поверхні обертання х² + у² = z.

Внутрішній інтеграл

,

оскільки він дорівнює площі круга. Отже,

.

Зауваження. Якщо область V – прямокутний паралелепіпед то формула (4) приймає вигляд:

. (8)

Якщо підінтегральна функція неперервна в області V, то у формулі (8) змінні інтегрування х, у, z можна міняти місцями:

Якщо підінтегральна функція є добутком трьох функцій , то трикратний інтеграл правої частини рівності (8) буде дорівнювати добутку трьох відповідних визначених інтегралів.

Приклад 7. Обчислити інтеграл , якщо область V обмежена поверхнями , , , х + у + z = 3.

Розв’язання. Область інтегрування V зобразимо на мал. 7. Визначимо аналітичний опис заданої області V. Для визначення меж змінної z проведемо через область V пряму, яка паралельна осі Oz. Тоді одержимо: .

Для опису області D виберемо сталі межі зміни х: . Тоді y буде змінюватись в межах: .

z x y 3 3 3 0 D z=3–x–y y=3–x

Мал.7

За формулою (4) перейдемо від заданого потрійного інтеграла до трикратного інтеграла:

Отже, область V має аналітичний опис:

=

.

Приклад 8. Обчислити об’єм області, обмеженої еліпсоїдом

Розв’язання. Згідно властивості 6 інтеграла по області шуканий об’єм v області V знайдемо за формулою:

.

Область V обмежена знизу поверхнею ,

а зверху поверхнею .

Область V проектується на площину хОу в область D, яка обмежена еліпсом .

Тому область V аналітично описується нерівностями:

.

За формулою (4) одержимо:

Для обчислення внутрішнього інтеграла зробимо підстановку

При такій підстановці t змінюється від до . Одержимо:

.

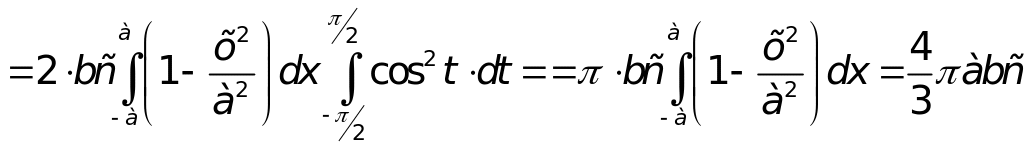Отже, об’єм еліпсоїда .

Якщо а = b = с, то одержимо об’єм кулі .

Приклад 9. Обчислити масу області V, якщо густина розподілу маси , а область V є циліндром , .

Розв’язання. Згідно пункту 12.1.4 шукану масу m знайдемо за формулою:

.

Будемо шукати масу чверті циліндра і одержаний результат помножимо на 4. Тоді

.