- •12.1. Інтеграли по області, їх властивості, різновиди та деякі застосування
- •12.1.1. Визначення інтеграла
- •12.1.2. Основні властивості інтеграла по області
- •12.1.3. Різновиди інтегралів по області
- •12.1.4. Деякі застосування інтегралів по області
- •12.2.1. Обчислення криволінійних інтегралів першого роду
- •4. Обчислити сумарний електричний заряд, який розподілений з густиною на дузі ав: .
- •12.3.1. Обчислення подвійних інтегралів
- •12.3.2 Заміна змінних в подвійному інтегралі
- •9. Застосування подвійних інтегралів
- •12.4 Обчислення поверхневих інтегралів першого роду
- •12.4.1. Основні поняття
- •12.5. Обчислення потрійних інтегралів
- •12.5.1. Основні поняття
- •12.5.2. Заміна змінних в потрійному інтегралі
- •12.6. Невластиві інтеграли по області
- •12.6.1. Основні поняття
4. Обчислити сумарний електричний заряд, який розподілений з густиною на дузі ав: .
12.3.1. Обчислення подвійних інтегралів
Якщо область D на площині хОу правильна в напрямку осі Оу (див. мал. 1, а), то її аналітично можна описати нерівностями виду
 (1)
(1)
і подвійний інтеграл зводиться до повторного за формулою:
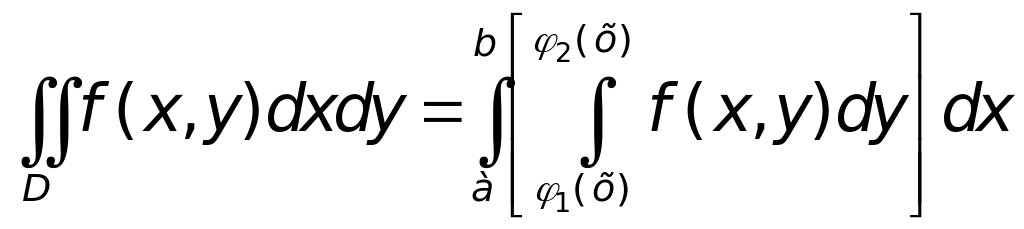 .
(2)
.
(2)
Якщо область D на площині хОу правильна в напрямку осі Ох (див. мал. 1, б), то її аналітично можна описати нерівностями виду
 (3)
(3)
і подвійний інтеграл зводиться до повторного за формулою:
 (4)
(4)
Якщо область D на площині хОу правильна в напрямі осі Оу і в напрямі осі Ох (див. мал. 1, в), тоді мають місце рівності:
 ,
(5)
,
(5)
які означають, що подвійний інтеграл в цьому випадку можна обчислити за формулою (2) або (4).
Для обчислення повторного інтеграла треба спочатку за формулою Ньютона-Лейбніца знайти внутрішній інтеграл за відповідною змінною інтегрування, а потім обчислити зовнішній інтеграл за іншою змінною інтегрування.

Y Y

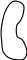

![]() d
d


![]()
D

![]() D
D
![]()

a 0 b x 0 x
c

 Y
Y
в) D Мал.1

0 X
Приклад
2.
Визначити сумарний заряд Q пластинки,
що обмежена лініями у
= х2,
у2
= х,
4х
+ 4у
– 3 = 0, якщо щільність розподіленого
поверхневого заряду
![]() .
.
Розв’язання. Згідно фізичному значенню інтеграла по області маємо:
![]() .
.
Область
інтегрування D
зображена на мал. 2. Щоб одержати
аналітичний опис заданої пластинки у
вигляді нерівностей (3) розіб’ємо D
на дві частини D1
та D2
прямою
![]() ,
яка проходить паралельно осі Ох через
точку перетину заданої прямої і параболи
,
яка проходить паралельно осі Ох через
точку перетину заданої прямої і параболи
![]() .
Використовуючи властивості інтеграла
по області отримаємо:
.
Використовуючи властивості інтеграла
по області отримаємо:
![]()



y



![]()
![]()

![]() 4x+4y-3=0
4x+4y-3=0
![]()
![]()
![]()
![]() x
x

![]()
Мал.2
З малюнка 2 одержуємо аналітичний опис областей:

 .
.
Для цього в кожній області спочатку визначили сталі межі змінної у, а потім – нерівності для х шляхом визначення значень х, якщо рухатися через область за напрямом осі Ох.
Отже,


 (од.
зар.).
(од.
зар.).
12.3.2 Заміна змінних в подвійному інтегралі
При
заміні змінних:
![]() ,
,
![]() область D
площини хОу
відображається в область G
площини uОv;
елемент площини dxdy
відобразиться в елемент площі
область D
площини хОу
відображається в область G
площини uОv;
елемент площини dxdy
відобразиться в елемент площі
![]() ,
де визначник
,
де визначник

називають функціональним визначником або якобіаном, а його модуль називають коефіцієнтом спотворення області.
Отже,
якщо функції
![]() та
та
![]() неперервні в області G
разом із своїми частинними похідними
першого порядку, то має місце рівність
неперервні в області G
разом із своїми частинними похідними
першого порядку, то має місце рівність
![]() .
.
Часто
для обчислення подвійних інтегралів
використовують полярні координати:
![]() ,
,
![]() .
Тоді якобіан переходу
.
Тоді якобіан переходу
![]() ,
а елемент площі
,
а елемент площі
![]() .
.
Перехід
в подвійному інтегралі до полярних
координат доцільно використовувати в
тих випадках, коли підінтегральна
функція залежить від х2
+ у2
або від
![]() ,
а також у випадках, коли межа області D
містить дуги кіл та промені, що виходять
із початку координат.
,
а також у випадках, коли межа області D
містить дуги кіл та промені, що виходять
із початку координат.
Приклад
3.
Обчислити інтеграл
![]() ,
по чверті кільця
,
по чверті кільця
![]() ,
що лежить в першому квадранті.
,
що лежить в першому квадранті.
Розв’язання. Область інтегрування D зобразимо на мал. 3.
Підставимо
в нерівність
,
замість х
та у
їх значення
,
.
Одержимо:
![]() .
Оскільки
кільце лежить в першому квадранті, то
.
Оскільки
кільце лежить в першому квадранті, то
![]() .
.
Отже
y
x
2
1
1
2
0
Мал. 3 |
|

![]()
Зауваження. При переході до полярних координат в подвійному інтегралі треба враховувати, що в точці О(0,0) якобіан дорівнює нулю. Так, для області D, що зображена на малюнку 4, перехід до повторного інтегралу приймає вид:

y
x
D
0
Мал. 4 |

1. Обчислити повторні інтеграли:
а)
 ;
б)
;
б)
 ;
в)
;
в)
![]() ;
;
г)
 ;
д)
;
д)
 ;
е)
;
е)
 .
.
2. Записати рівняння ліній, що обмежують області інтегрування заданих інтегралів та зобразити ці області:
а)
 ;
б)
;
б)
 ;
в)
;
в)
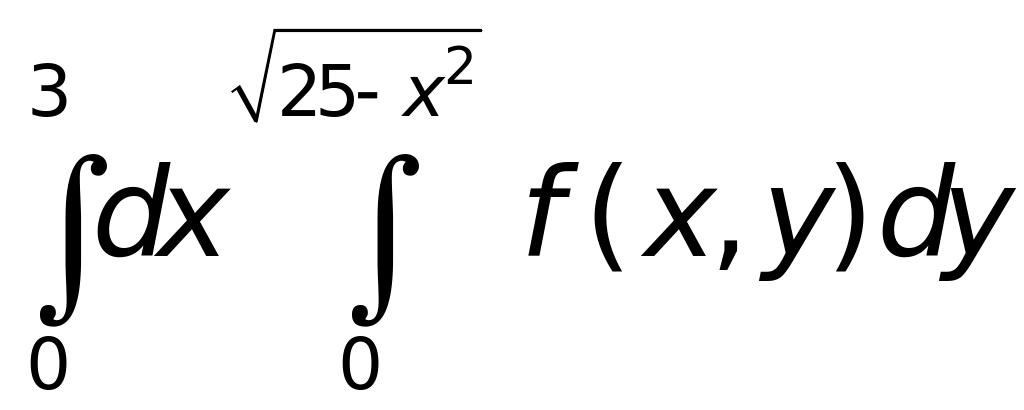 ;
;
г)
 ;
д)
;
д)
![]() .
.
3. Перейти від подвійного інтеграла до повторного:
а) D – трикутник з вершинами O(0, 0), А(1, 0), В(1, 1).
б) D – трапеція з вершинами O(0, 0), А(2, 0), В(1, 1), С(0, 1).
в) D – паралелограм з вершинами А(1, 5), В(2, 4), С(2, 7), D(1, 5).
г) D – параболічний сегмент, що обмежений параболою
у = х2 та відрізком, який з’єднує точки параболи В(–1, 2) та
А(1, 2).
д) D – кругове кільце, що обмежене колами радіусів r = 1 та R = 3 із загальним центром O(0, 0).
4. Змінити порядок інтегрування
а)
 ;
б)
;
б)
 ;
в)
;
в)
![]() .
.
5.
Обчислити інтеграл
![]() ,
якщо
,
якщо
а) D – трикутник з вершинами O(0, 0), А(1, 1) та В(0, 1);
б) D – обмежена прямою, що проходить через точки
А(2, 0) та В(0, 2), і дугою кола з центром в точці С(0, 1), радіуса 1.
6.
Обчислити інтеграл
![]() ,
де D
– область, що обмежена лініями у2
= х,
х
= 0, у
= 1.
,
де D
– область, що обмежена лініями у2
= х,
х
= 0, у
= 1.
7.
Обчислити
![]() ,
де D
– область, що обмежена лініями
,
де D
– область, що обмежена лініями
![]() ,
у
= х.
,
у
= х.
8. Використовуючи перехід до полярних координат, обчислити інтеграли:
а)
![]() ,
D
– півкруг радіуса а
з центром в початку координат, що лежить
вище осі Ох.
,
D
– півкруг радіуса а
з центром в початку координат, що лежить
вище осі Ох.
б)
 ;
;
в)
 ,
D
– визначається нерівностями
,
D
– визначається нерівностями

г)
![]() ,
D – частина кільця
,
D – частина кільця

д)
![]() ,
D
– круг
,
D
– круг
![]() .
.