12.1. Інтеграли по області, їх властивості, різновиди та деякі застосування

12.1.1. Визначення інтеграла

Нехай в замкненій області D задана функція .

Область D довільним чином розіб’ємо на n частин

D₁, D₂, ... , D_n і в кожній частині візьмемо довільну точку: М₁, М₂, ... , М_n. Позначимо міру частини D_і, діаметром d_i, а через – максимальний діаметр частин D₁, D₂, ... , D_n, тобто .

Інтеграл по області D визначається як границя інтегральної суми за формулою

(1)

Якщо інтеграл від функції по області D існує, то ця функція зветься інтегрованою в області D.

Достатньою умовою інтегрованості функції в замкненій обмеженої області D є її неперервність в цій області.

12.1.2. Основні властивості інтеграла по області

Основні властивості інтеграла по області аналогічні властивостям визначеного інтеграла. Вкажемо ці властивості при умові інтегрованості відповідних функцій.

1. Якщо область D розбити на дві області D₁ та D₂ без спільних внутрішніх точок, тоді

.

2. Сталий множник можна виносити за знак інтеграла.

3. Інтеграл по області D від алгебраїчної суми скінченої кількості функцій дорівнює такій самій алгебраїчній сумі від кожної з цих функцій:

.

4. Якщо у довільній точці , то виконується нерівність

.

5. .

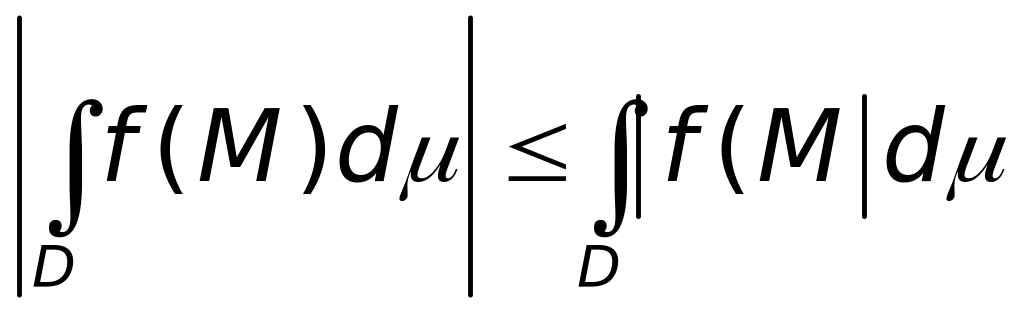6. Якщо підінтегральна функція , то інтеграл від такої функції по області D дорівнює мірі області

. (2)

7. Оцінка інтеграла по області. Якщо , то

.

8. Теорема про середнє. Якщо неперервна в замкненій області D, то в цій області знайдеться хоча б одна така точка М₀, що буде виконуватись рівність

.

12.1.3. Різновиди інтегралів по області

Інтегралам по області надають спеціальні назви і позначення в залежності від типу області.

Якщо областю інтегрування є дуга АВ кривої L, то інтеграл називають криволінійним інтегралом першого роду і позначають так:

.

Оскільки мірою лінійної множини є довжина, то під знаком інтеграла замість пишуть . Якщо дуга АВ – плоска і лежить в площині хОу, тоді точка М дуги АВ має координати (х, у), тому

(3)

Якщо дуга АВ просторова, то , тому

(4)

Криволінійний інтеграл першого роду не залежить від напряму інтегрування:

. (5)

Якщо областю інтегрування буде деяка поверхня S, тоді інтеграл називають поверхневим інтегралом першого роду і позначають .

Оскільки мірою поверхневої множини є площа, то під знаком інтеграла замість пишуть . Два знаки інтеграла вказують, що інтегрування ведеться по двовимірній області. Якщо поверхня S не плоска, тоді і тому

(6)

Якщо область інтегрування є плоскою поверхнею D, то ,

(7)

Такий інтеграл називають подвійним інтегралом.

Інтеграл по просторовій області V називають потрійним інтегралом і позначають так:

.

Оскільки , , то існують і такі позначення потрійного інтеграла:

. (8)

Існують ще криволінійні та поверхневі інтеграли другого роду, які є різновидами інтеграла по орієнтованій області від вектор-функції.

Їх позначають так:

, , . (9)

де – нормаль до поверхні S.

Криволінійний інтеграл 2 роду змінює свій знак при зміні напряму інтегрування:

.

Аналогічну властивість мають поверхневі інтеграли другого роду.

Оскільки різні сторони поверхні відповідають різним напрямкам нормалі, то інтеграли, у яких областями інтегрування є різні сторони поверхні S, відрізняються знаками.