35B/Тригонометрическая и показательная формы

Если вещественную x и мнимую y части комплексного числа выразить через модуль r = | z | и аргумент (x = rcos φ, y = rsin φ), то всякое комплексное число z, кроме нуля, можно записать в тригонометрической форме

z = r(cos φ + isin φ).

Сложение, вычитание, умножение и деление комплексных чисел.

Определение 1. Суммой двух комплексных чисел c1=(a1;b1), c2=(a2;b2) называют комплексное число c=c1+c2=(a1+a2;b1+b2).

Определение 2. Разностью двух комплексных чисел c1=(a1;b1), c2=(a2;b2) называют комплексное число c=c1+(-c2)=(a1-a2;b1-b2).

Определение 3. Произведением комплексного числа c=(a;b) на действительное число , называют комплексное число c=( a; b).

Определение 4. Произведением двух комплексных чисел c1=(a1;b1), c2=(a2;b2) называют комплексное число c=(a1*a2-b1*b2;a1*b2+a2*b1).

Возведение в степень.

Из операции умножения комплексных чисел следует, что

В общем случае получим: ,

где n – целое положительное число.

  Это выражение называется формулой Муавра.

36в

Извлечение корня есть действие, обратное возведению в степень. Поэтому (см. предыдущий параграф) модуль корня (целой степени) из комплексного числа получается извлечением корня той же степени из модуля подкоренного числа, а аргумент – делением аргумента на показатель корня:

(В)

Корень n-й степени из всякого комплексного числа имеет n различных значений. Все они Все они имеют одинаковые модули ; аргументы же получаются из аргумента одного из них последовательным прибавлением угла (1/n)*360°. Действительно, пусть φ0 есть аргумент подкоренного числа. Тогда φ0 + 360°; φ0 +2•360° и т. д. также являются его аргументами. Формула (В) показывает, что за аргумент корня можно принять не только , но также 360°, 360° и т. д. Соответствующие значения корня не все различны между собой: аргумент 360, т. е. +360°, дает то же комплексное число, что и аргумент ; аргумент 360° = 360°+360° дает то же комплексное число, что и аргумент 360°, и т.д. Различных значений корня будет ровно n. См. примеры. Пример 1. Извлечь квадратный корень из числа – 9i. Модуль этого числа есть 9. Значит, модуль корня равен Аргумент подкоренного числа можно принять равным - 90°, - 90°+360°, - 90°+2•360° и т. д. В первом случае получаем:

(1)

Во втором случае

(2)

В третьем случае

т. e. то же, что в первом. Беря φ = - 90° + 3 • 360°, - 90° + 4 • 360° или φ = - 90° - 360°; - 90° - 2•360° и т. д., мы будем поочередно получать значения (1) и (2). Пример 2. Извлечь квадратный корень из числа 16. Аргумент этого числа есть 360°k (k – целое число). Аргумент корня будет 360 k : 2 = 180k. Если k есть нуль или четное число, то аргумент корня равен нулю или кратен 360°. Тогда 16^1/2= 4 (cos 0° +isin 0°) = 4. Если же k – нечетное число, то аргумент будет 180° или отличаться от 180° на кратное 360°. Тогда 16^1/2 = 4 (соs 180° + isin180°) = - 4. Пример 3. Извлечь кубический корень из 1. Модуль корня равен Аргумент подкоренного числа есть 360k (k –любое целое число). Аргумент корня будет 120°k. Полагая k = 0,1,2, находим три значения аргумента корня: 0°, 120°, 240°. Соответствующие значения корня будут*: z1 = cos 0° + isin 0° = 1, z2 = cos 120° + isin 120° = z3 = cos 240° + isin 240° = Н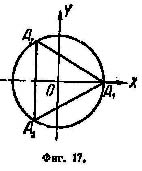 а фиг. 17 эти значения изображены точками A1, A2, A3. Треугольник A1A2A3 – равносторонний. Он вписан в окружность радиуса 1. Пример 4. Извлечь корень шестой степени из -1. Аргумент подкоренного числа -1 есть 180° + 360°k. Аргумент корня равен 30° + 60°k. 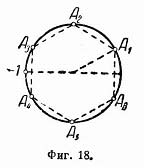Имеем следующие шесть значений корня: z1 = cos 30° + isin 30° = z2 = cos 90° + isin 90° = i, z3 = cos 150° + isin 150° = _ z4 = cos 210° + isin 210° = _ z5 = cos 270° + isin 270° = - i, z6 = cos 330° + isin 330° = _ Точки A1, A2, A3, A4, A5, A6, изображающие эти значения (фиг. 18), являются вершинами правильного шестиугольника.

Из формулы (В) следует, что n корней из какого-либо комплексного числа и n корней из сопряженного числа попарно сопряжены. Пример 5. Корни четвертой степени из числа 16(cos120° + isin120°) = - 8 + будут: z1 = 2(cos 30° + isin 30°) = + i; z2 = 2(cos 120° + isin 120°) = -1 + i; z3 = 2(cos 210° + isin 210°) = _ - i; z4 = 2(cos 300° + isin 300°) = 1 - i, а корни той же степени из числа 16 (cos120° - isin120°) = -8 - будут: = 2(cos 30° - isin 30°) = - i; = 2(cos 120° - isin 120°) = -1 - i; = 2(cos 210° - isin 210°) = - + i; = 2(cos 300° - isin 300°) = 1 + i. Числа z1 и , z2 и и т. д. попарно сопряжены. *Эти результаты полезно проверить. Помножив число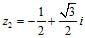 само на себя по правилу § 38, найдем 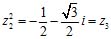. Помножая еще раз, получим Так же проверяется и корень . Именно ,

Корни n-й степени из единицы — комплексные корни многочлена . Другими словами, это комплексные числа, n-я степень которых равна 1.

Представим комплексную единицу в тригонометрическом виде:

Тогда по формуле Муавра, получим:

Здесь u_k — корни из единицы.

Корни из единицы могут также быть представлены в показательной форме:

Из этих формул вытекает, что корней из единицы всегда ровно n, и все они различны.