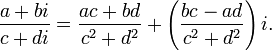Определение

Пусть  — тройка непустых множеств. Бинарной операцией или двуме́стной опера́цией в паре со значениями в C называется отображение , где

Если A = B = C, то действие называется внутренним, если A = C или B = C — внешним. В частности, любое внутреннее действие является внешним.

Замечание

Бинарную операцию принято обозначать знаком действия, который ставится между операндами (инфиксная форма записи). Например, для произвольной бинарной операции результат её применения к двум элементам x и y записывается в виде .

Это не значит, что не используются другие формы записи бинарных операций. Существуют и другие виды записи:

Примеры

Примерами бинарных операций могут служить сложение, умножение и вычитание на поле вещественных чисел. Сложение и умножение чисел являются коммутативными и ассоциативными операциями, а вычитание — нет.

Гру́ппа  — непустое множество с определённой на нём бинарной операцией, удовлетворяющей указанным ниже аксиомам. Группы являются важными инструментами в изучении симметрии во всех её проявлениях. Примерами групп являются вещественные числа с операцией сложения, множество вращений плоскости вокруг начала координат и т. п. Ветвь математики, занимающаяся группами, называется теорией групп.

Непустое множество G с заданной на нём бинарной операцией называется группой (G, * ), если выполнены следующие аксиомы:

1. ассоциативность: ;

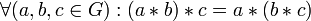2. наличие нейтрального элемента: ;

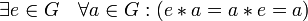3. наличие обратного элемента:

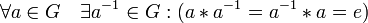
(Внутренним) законом композиции на множестве называется отображение . Элемент называется нейтральным, если Элемент называется симметричным элементу , если

Непустое множество R называется кольцом, если в нем определены две алгебраические операции: сложение, ставящее в соответствие каждым двум элементам a, b элемент a + b, называемый их суммой, и умножение, ставящее в соответствие каждым двум элементам a, b элемент ab, называемый их произведением, причем эти операции обладают следующими свойствами:

     I. (Коммутативность сложения) a + b = b + a;

     II. (Ассоциативность сложения) a + (b + c) = (a + b) + c;

     III. (Обратимость сложения) Для любых a и b из R уравнение a + x = b имеет (по крайней мере одно) решение, т. е. существует элемент такой, что a + c = b;

     IV. (Коммутативность умножения) ab = ba;

     Термин "кольцо" применяется также ко множествам с некоммутативным или даже неассоциативным умножением. Формулировки других свойств также меняются.

     V. (Ассоциативность умножения) a(bc) = (ab)c;

     VI. (Дистрибутивность умножения относительно сложения) (a + b)c = ac + bc.

     Примеры колец. При обычных операциях сложения и умножения кольцом является:

     1. Множество целых чисел.

     2. Множество рациональных чисел.

     3. Множество действительных чисел.

     4. Множество рациональных чисел.

34B

Ко́мпле́ксные^[1] чи́сла (устар. Мнимые числа^[2]), — расширение множества вещественных чисел, обычно обозначается . Любое комплексное число может быть представлено как формальная сумма x + iy, где x и y — вещественные числа, i — мнимая единица^[3].

Комплексные числа образуют алгебраически замкнутое поле — это означает, что многочлен степени n с комплексными коэффициентами имеет ровно n комплексных корней (основная теорема алгебры).

Построение поля комплексных чисел.

   Пусть  – декартов квадрат поля действительных чисел, т.е.  – множество упорядоченных пар действительных чисел. Определим на этом множестве две внутренние бинарные алгебраические операции – сложение и умножение по следующим правилам:  положим по определению

(1)              

(2)            .

Очевидно, что сумма и произведение двух пар из  снова есть пара из множества , т.к. сумма, произведение и разность действительных чисел есть действительные числа. Таким образом,  – алгебраическая структура с двумя внутренними бинарными алгебраическими операциями.

Теорема.  – поле.

• Сравнение

a + bi = c + di означает, что a = c и b = d (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).

• Сложение

(a + bi) + (c + di) = (a + c) + (b + d)i.

• Вычитание

(a + bi) − (c + di) = (a − c) + (b − d)i.

• Умножение

• Деление