Скалярное произведение в произвольном базисе
Пусть
-
базис евклидова пространства
,
,
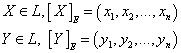рассмотрим скалярное произведение:
=
(*)
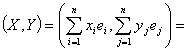
Если записать (*) в матричном виде, то получим:
.
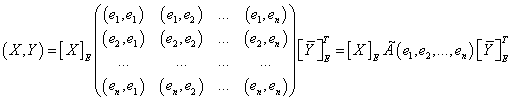Если базис
-
ортонормированный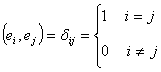, то
,
то
.
48\B
Ортогональное дополнение подпространства m из l
Пусть
-
евклидово (унитарное) пространство,
подпространство
.
Вектор
называется
ортогональным к подпространству
,
если для всех
.
Множество всех векторов
ортогональных
к подпространству
называется
ортогональным дополнением
и
обозначается
.
Очевидно, М┴
является подпространством пространства
,
причем для размерности подпространств
и
размерность пространства
связаны
соотношением
.
Действительно, выберем
базис 
подпространства
,
дополним его до базиса
,
получим
.
Ортогонализируем данный базис
методом Грамма-Шмидта, получим:
-
базис пространства
,
-
базис подпространства
,
-
базис подпространства
ортогонального дополнения
.
Говорят, что пространство
является
прямой ортогональной суммой своих
подпространств
и
:
Ортогональное дополнение подпространства m из l
Пусть - евклидово (унитарное) пространство, подпространство . Вектор называется ортогональным к подпространству , если для всех .
Множество всех векторов ортогональных к подпространству называется ортогональным дополнением и обозначается .
Очевидно, М┴ является подпространством пространства , причем для размерности подпространств и размерность пространства связаны соотношением
.
Действительно, выберем базис подпространства , дополним его до базиса , получим . Ортогонализируем данный базис методом Грамма-Шмидта, получим: - базис пространства ,
- базис подпространства , - базис подпространства ортогонального дополнения .
Говорят, что пространство является прямой ортогональной суммой своих подпространств и :
49/B
Опера́тор (позднелат. operator — работник, исполнитель, от operor — работаю, действую) — то же, что отображение в математике.
Привычная функция отображает одно число (аргумент) на другое (значение функции). Функция нескольких переменных отображает вектор (ряд чисел) на число. В случае отображения вектора на вектор, отображение чаще называют оператором. А поскольку функции относятся к векторам (аргумент функции служит индексом, при этом количество элементов может достигать континуума для недискретных функций), операторы часто применяются к функциям. Таким образом оператор можно считать обобщением функции: если функция оперирует числами, возвращая число, то оператор принимает и возвращает ряд чисел, то есть оперирует функциями.
Наиболее часто встречающиеся операторы:
Функциональный анализ: Операторы на пространствах функций (дифференцирование, интегрирование, свертка с ядром, преобразование Фурье).
Линейная алгебра: Отображения (в особенности линейные) векторных пространств (проекторы, повороты координат, гомотетии, умножения вектора на матрицу).