[Править] Связанные определения

• Под евклидовой метрикой может пониматься метрика, описанная выше, а также соответствующая риманова метрика.

• Под локальной евклидовостью обычно имеют в виду то, что каждое касательное пространство риманова многообразия есть евклидово пространство со всеми вытекающими свойствами, например, возможностью (по гладкости метрики) ввести в малой окрестности точки координаты, в которых расстояние выражается (с точностью до какого-то порядка) в соответствии с описанным выше.

• Метрическое пространство называют локально евклидовым также если возможно ввести на нём координаты, в которых метрика будет евклидовой (в смысле второго определения) всюду (или хотя бы на конечной области) - каковым, например, является риманово многообразие нулевой кривизны.

[Править] Примеры

Наглядными примерами евклидовых пространств могут служить пространства:

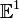• размерности 1 (вещественная прямая)

• размерности 2 (евклидова плоскость)

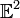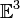• размерности 3 (евклидово трехмерное пространство)

• Евклидово пространство можно считать современной интерпретацией и обобщением (так как оно допускает размерности больше трех) классической (Евклидовой) геометрии.

Более абстрактный пример:

• пространство вещественных многочленов p(x) степени, не превосходящей n, со скалярным произведением, определенным как интеграл произведения по конечному отрезку (или по всей прямой, но с быстро спадающей весовой функцией, например )

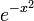п.5. Ортогональные векторы. Определение. Два вектора называются ортогональными, если угол между ними равен прямому углу, т.е. .

Обозначение:  – векторы  и  ортогональны.

Определение. Тройка векторов  называется ортогональной, если эти векторы попарно ортогональны друг другу, т.е. , .

Процесс ортогонализации Грама--Шмидта в конечномерном евклидовом пространстве

Определение 1.   Линейное пространство конечной размерности над полем называется унитарным, если для любых двух элементов определена комплекснозначная функция (скалярное произведение), обозначающаяся , удовлетворяющая свойствам:

1. (Коммутативность) ;

2. ;

3. ;

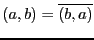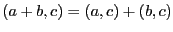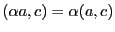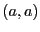4. -- вещественное .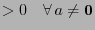

Определение евклидова пространства отличается тем, что поле заменяется на , а комплексное сопряжение в свойстве не требуется.

Теорема 1. (Грама--Шмидта)   в любом конечномерном унитарном (евклидовом) пространстве можно построить ортонормированный базис.

Доказательство. Докажем методом математической индукции.

База индукции. . . Это и есть ОНБ.

Предположение. Пусть верно для .

Доказательство индукции. Возьмем базис . Рассмотрим его в -мерном пространстве . По предположению, там найдется ОНБ . Дополним этот базис до базиса : (без ограничения общности, последний вектор линейно не зависит от этого базиса). Сконструируем вектор

Нужно, чтобы он был ортогонален всем векторам:

а это выполнено тогда и только тогда, когда (умножая обе части равенства на последовательно)

Отсюда, , . Теперь положим , построив тем самым ОНБ и доказав утрверждение теоремы.

47/B

Ортогональный (ортонормированный) базис — ортогональная (ортонормированная) система элементов линейного пространства со скалярным произведением, обладающая свойством полноты

Ортогональный базис — базис, составленный из попарно ортогональных векторов.

Ортонормированный базис удовлетворяет еще и условию единичности нормы всех его элементов. То есть это ортогональный базис с нормированными элементами.

Последнее удобно записывается при помощи символа Кронекера:

то есть скалярное произведение каждой пары базисных векторов равно нулю, когда они не совпадают ( ), и равно единице при совпадающем индексе, то есть когда берется скалярное произведение любого базисного вектора с самим собой.

Очень многое записывается в ортогональном базисе гораздо проще, чем в произвольном, поэтому очень часто стараются использовать именно такие базисы, если только это возможно или использование какого-то специального неортогонального базиса не дает особых специальных удобств. Или если не отказываются от него в пользу базиса общего вида из соображений общности.

Ортонормированный базис является самодуальным (дуальный ему базис совпадает с ним самим). Поэтому в нём можно не делать различия между верхними и нижними индексами, и пользоваться, скажем, только нижними (как обычно и принято, если конечно при этом используются только ортонормированные базисы).

Линейная независимость следует из ортогональности, то есть достигается для ортогональной системы векторов автоматически.

Коэффициенты в разложении вектора по ортогональному базису:

можно найти так:

.

Полнота ортонормированной системы векторов эквивалентна равенству Парсеваля: для любого вектора квадрат нормы вектора равен сумме квадратов коэффициентов его разложения по базису:

Аналогичные соотношения имеют место и для бесконечномерного случая (см. ниже).