3. Некоторые способы решения типичных тестовых и экзаменационных задач (3 семестр)

Математический анализ (иное название – дифференциальное и интегральное исчисление; старое название – анализ бесконечно малых) преподаётся студентам 300 лет.

Рекомендуем при решении задач входного теста следовать способам, терминам и обозначениям того «толстого» учебника, по которому студент готовился.

На тот случай, если нужные страницы в «толстом» учебнике оказались вырванными, ниже приводятся некоторые из способов решения типичных тестовых и экзаменационных задач.

П р и м е р  1. Найти выражение для –й частичной суммы числового ряда

и найти сумму этого ряда.

Р е ш е н и е. Шаг 1. Находим выражение для –й частичной суммы данного числового ряда. По определению

.

Общий член ряда – правильная рациональная функция от . Разложим общий член ряда на простые дроби:

.

Тогда для –й частичной суммы имеем:

.

Давая индексу последовательно значения 1, 2, 3 и , , , получим:

.

Отсюда имеем следующее выражение для –й частичной суммы:

.

Шаг 2. Согласно определению сумма ряда – предел последовательности его частичных сумм: . Тогда в силу шага 1 получаем:

.

О т в е т. .

П р и м е р  2. Найти сумму числового ряда

.

Р е ш е н и е. Шаг 1. Сводим данный числовой ряд к разности двух геометрических рядов. Последовательно имеем:

.

Шаг 2. Воспользуемся следующей известной формулой суммы геометрического ряда:

.

Тогда с учётом шага 1 сумма данного ряда

.

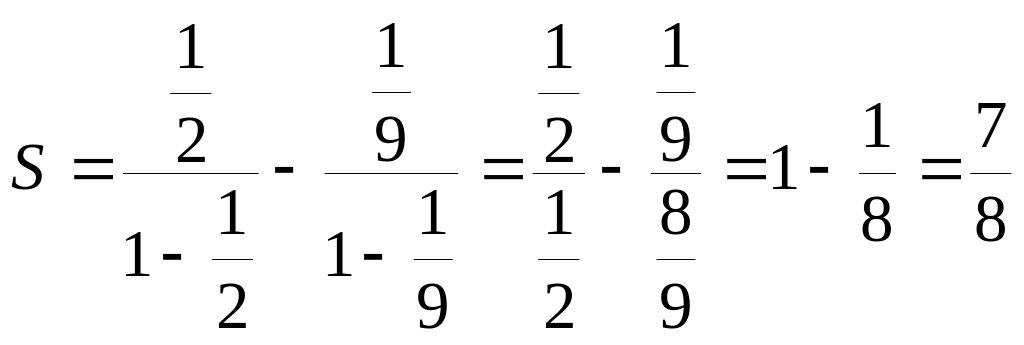О т в е т. .

П р и м е р  3. Найти разложение в степенной ряд по степеням х решения дифференциального уравнения , (записать три первых, отличных от нуля, члена этого разложения).

Р е ш е н и е. Искомое разложение ищем в виде ряда Тейлора с центром разложения (в виде ряда Маклорена):

,

в котором по условию .

Перепишем дифференциальное уравнение с указанием аргумента: . Тогда значение первой производной .

Согласно определению . Тогда вторая производная

.

Её числовое значение

.

Подставляем данное значение и найденные значения и в записанный выше ряд Тейлора с центром разложения и получаем следующий ответ.

О т в е т. .

П р и м е р  4. По формуле , в которой дискретный параметр пробегает натуральные значения =1, 2, 3, …, методом интегрирования по частям вычислить синус-коэффициенты Фурье функции

Р е ш е н и е. Разбиваем отрезок интегрирования на два: и . Тогда для синус-коэффициентов Фурье данной функции имеем:

.

Воспользуемся формулой интегрирования по частям:

.

Тогда последовательно получаем:

.

С учётом значений тригонометрических функций , , и , для синус-коэффициентов Фурье данной функции имеем:

.

Отсюда для соответственно чётного и нечётного получаем следующий ответ.

О т в е т.

П р и м е р  5. Вычислить поверхностный интеграл первого рода

,

где поверхность S – часть плоскости

x+2y+z-2=0,

отсеченная координатными плоскостями.

Р е ш е н и е. Из данного общего уравнения плоскости получаем уравнение плоскости «в отрезках»:

.

Строим поверхность S – треугольник .

z	C(0; 0; 2) O(0; 0; 0) y
A(2; 0; 0) x	B(0; 1; 0)

Сводим вычисление поверхностного интеграла первого рода (по площади) по поверхности пространственного треугольника к вычислению двойного интеграла в координатной плоскости Оху.

Находим явное уравнение поверхности S:

.

Тогда элемент площади

и искомый интеграл

.

Вычисление последнего двойного интеграла по треугольнику (проекции пространственного треугольника на плоскость Оху) сводим к вычислению повторного (двукратного) интеграла.

В плоскости Оху (z=0) общее уравнение стороны АВ имеет вид: x+2y-2=0. Отсюда имеем для неё явное уравнение х=-2у+2. Тогда искомый интеграл

.

Вычисляем внутренний интеграл:

=

= =

= .

Вычисляем внешний интеграл:

.

О т в е т. .

П р и м е р  6. Найти дивергенцию дифференцируемого векторного поля

.

По формуле Остроградского – Гаусса вычислить поток этого векторного поля через внешнюю поверхность пирамиды, образуемую плоскостью

2x+3y+z-6=0

и координатными плоскостями.

Р е ш е н и е. Шаг 1. По определению дивергенция

.

Шаг 2. Из общего уравнения плоскости 2x+3y+z-6=0 получаем уравнение плоскости «в отрезках»:

.

Строим пирамиду ОАВС.

z	C(0; 0; 6) O(0; 0; 0) y
A(3; 0; 0) x	B(0; 2; 0)

Шаг 3. По теореме Остроградского – Гаусса поток векторного поля через поверхность пирамиды ОАВС в направлении вектора внешней нормали равен тройному интегралу от дивергенции по объёму этой пирамиды ОАВС:

.

Геометрический смысл последнего тройного интеграла – объём пирамиды ОАВС. Тогда поток

.

Объём пирамиды ОАВС равен одной шестой объёма прямоугольного параллелепипеда со сторонами ОА, ОВ и ОС:

.

Итак, поток

.

О т в е т. ; .

П р и м е р  7. Найти ротор дифференцируемого векторного поля

.

По формуле Стокса вычислить циркуляцию этого векторного поля по контуру треугольника, полученного в результате пересечения плоскости

3x+2y+2z-6=0

с координатными плоскостями, при положительном направлении обхода относительно нормального вектора данной плоскости.

Р е ш е н и е. Шаг 1. По определению ротор

.

Символический определитель третьего порядка раскладываем по элементам верхней строки:

.

Вычисляем символические определители второго порядка:

.

Последовательно имеем:

.

Шаг 2. Из общего уравнения плоскости 3x+2y+2z-6=0 получаем уравнение плоскости «в отрезках»:

.

Строим замкнутый контур АВСА.

z	C(0; 0; 3) O(0; 0; 0) y
A(2; 0; 0) x	B(0; 3; 0)

Шаг 3. По теореме Стокса циркуляция векторного поля вдоль замкнутого контура АВСА равна потоку ротора через поверхность треугольника , натянутого на этот контур АВСА, в направлении вектора :

,

где точка « » обозначает скалярное умножение. Скалярное произведение векторов равно сумме произведений одноимённых координат. Поэтому циркуляция

.

Сводим вычисление предыдущих поверхностных интегралов второго рода (по координатам) к вычислению двойных интегралов (в одноимённых координатных плоскостях). Так как углы и - острые, то изменения знака при переходе от поверхностных интегралов к двойным интегралам не происходит и циркуляция

.

Геометрический смысл последних двойных интегралов – площади прямоугольных треугольников и . Тогда циркуляция

.

Площадь прямоугольного треугольника равна одной второй произведения длин его катетов:

.

Итак, циркуляция

.

О т в е т. ; .

П р и м е р  8. Является ли функция действительной частью аналитической функции. Если да, то найти аналитическую функцию при условии, что .

Р е ш е н и е. Шаг 1. Выясняем, удовлетворяет ли данная функция дифференциальному уравнению Лапласа.

Последовательно находим частные производные первого и второго порядков функции по и по :

;

.

Тогда

во всей плоскости .

Итак, функция удовлетворяет дифференциальному уравнению Лапласа во всей плоскости , т. е. является гармонической во всей плоскости .

Следовательно, функция является действительной частью аналитической во всей комплексной плоскости функции (является действительной частью целой функции ).

Шаг 2. Находим гармоническую функцию , сопряжённую к гармонической функции .

Из условий Коши – Римана

и шага 1 получаем следующую систему дифференциальных уравнений для нахождения функции :

.

Интегрируем верхнее уравнение последней системы по :

,

где - произвольная функция от . Полученное выражение для функции дифференцируем по :

.

Отсюда с учётом нижнего уравнения последней системы получаем уравнение

,

из которого находим, что

.

Последнее уравнение интегрируем по :

,

где - произвольная постоянная.

Итак, искомая гармоническая во всей плоскости функция

.

Шаг 3. Искомая аналитическая во всей комплексной плоскости функция найдена с точностью до постоянной:

.

Отсюда, с одной стороны, имеем:

.

С другой стороны, по условию

.

При сравнении последних двух правых частей получаем значение .

О т в е т. .

Если учесть, что

=

= ,

то ответ можно записать в следующем виде:

.

Ещё раз рекомендуем при решении задач входного теста следовать способам, терминам и обозначениям того «толстого» учебника, по которому студент готовился.