28.A. Тэарэмы Ойлера, Фэрма і Вільсана (без доказаў).

Тэарэма1. Функцыя Ойлера – мультыплікатыўная, г.зн 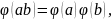калі (a,b)=1

Тэарэма2.(Ойлера)

Няхай , n-натуральны, (a, n)=1, тады

а^f⁽ⁿ⁾=1(mod n)

Тэарэма3.(Малая тэарэма Фэрма)

Няхай р-просты лік. Тады для адвольнага ,

а^р а(mod p)

Тэарэма4.(Вільсана)

Лік р-просты к.і.т.к (р-1)! -1(mod p)

30.A. Тэарэма пра існаванне кораня (без доказу). Поле раскладу паліному.

Тэарэма1(пра існаванне кораня):Для адвольнага поля Р і адвольнага паліному ненулявой ступені f(x)℮P[x]. Існуе пашырэнне поля Р, у якім ёсць прынамсі адзін корань паліному f(x).

Вынік: Існуе пашырэнне поля Р, у якім паліном f(x) раскладаецца на лінейныя множнікі.

α₁,α₂,…, α_n℮F, f(α_i)=0, i=1,…,n

P(α₁,α₂,…, α_n) называецца полем раскладу f(x) над P.

Тэарэма2: Для адвольнага паліному ненулявой ступені над полем P існуе поле раскладу.

32.A. Алгебрычныя і трансцэндэнтныя элементы. Поле алгебрычных элементаў. Алгебрычная замкнёнасць поля алгебрычных лікаў (без доказаў).

Тэарэма1. P алгебрычны над Р к.і.т.к [P(a): P]< .

У гэтым выпадку [P(a): P] роўная ступені мінімальнага палінному элемента а над полем Р

Тэарэма2. Няхай F пашырэнне поля Р. А- мноства элементаў з F, алгебрычных над Р.Тады А-падполе поля F, A P

Азн1. Поле наз алгебрычна замкнёным, калі адвольны паліном ненулевой ступені над Р мае корань у поле Р

Тэарэма3. Поле алгебрычна лікаў алгебраічна замкнёнае.Гэта зн, што адвольнаы корань паліному ненулявой ступені, каэфіцыенты якога алгебрычныя лікі, ёсць алгебрычны лік.

Тэарэма4. Поле алгебрычных лікаў злічанае

_Азн2. Элемент а Р наз алгебрычным над Р ,калі існуе ненулявы элемент 0 f(x) _P_[_x_]_f₍_a_)=0,_{трансцэндэнтным
над Р, калі такого паліному няма}