14. A. Група. Азначэнне, прыклады, уласцівасці. Два крытэры падгрупы.

Азн.1: , на якім вызначаны бінарная алгебрычная аперацыя •, наз. групай , калі выконваюцца наступныя аксіёмы:

1.Аперацыя • асацыятыўная, г.зн.

2.Існуе нейтральны элемент у дачыненні да аперацыі •, г.зн. такі элемент, што

;

існуе сіметрычны элемент, г.зн. такі элемент што .

Прыклады:1).Няхай F – поле, GL(n,F) - мноства ўсіх незвыродных матрыцаў ступені n над F. Тады на гэтым полі вызначана аперацыя множання det(a*b)=deta*detb≠0, калі a,b GL(n,F). Аперацыя асацыятыўна, ёсць адзінкавая матрыца у гэтым полі, такая, што ,

2).Няхай – мноства ўсіх біекцый . Падстановы . На вызначана аперацыя множання. Яна асацыятыўная, таму што множанне адвольных адлюстраванняў асацыятыўна, тоеснае адлюстраванне, такое, што Азн. 2: наз. падгрупай групы G, калі H –група ў дачыненні да аперацыяў, вызначаных ў G. Абазначаецца H<G.

Тэарэма 1 (1 крытэр падгрупы): 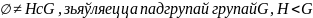к.іт.к : .

Тэарэма 2 (2 крытэр падгрупы): к.іт.к. .

Азн.3: Няхай –групы з аперацыямі • і * адпаведна. Біекцыя адлюстравання наз. Ізамарфізмам G на , калі: .

Калі існуе які-небудзь ізамарфізм групы G на будзем казаць,што G ізаморфны ( ).

Уласцівасці ізамарфізмаў групаў:

– ізамарфізм (адвольная група ізаморфная сама сабе)

2.Калі – ізамарфізм, - ізамарфізм, тады – ізамарфізм;

3.Калі , - ізамарфізмы групаў, тады – ізамарфізм ( ).

15. A. Спараджальнае мноства (сістэма ўтваральных) падгрупы. Цыклічная група. Падгрупы цыклічнай групы.(8)

Сцв.1: Перасячэнне адвольнага мноства падгрупаў групы G ёсць падгрупа групы G.

Азн.1: Няхай M падмноства групы G, перасячэнне ўсіх падгрупаў групы G, якія змяшчаюць H. Будзем абазначаць і наз. падгрупай спароджаных M. Само M наз. спараджальным мноствам (ці мноствам утваральных) падгрупы (M). Відавочна (M) ёсць найменшая падгрупа групы G, якая змяшчае M, г.зн. калі .

Тэарэма 1: Няхай . Падгрупа спараджальная

.

Азн.2: Група спароджаных аднаэлементавым мноствам элементаў наз. цыклічнай .

Вызначым ступені элемента a наступным чынам: . Паводле тэарэмы 1 цыклічная група спароджаныхт . Магчымы выпадкі:

1)

Азн.3: Парадкам наз. найменшы натуральны такі, што . Калі такога n няма, тады a наз. элементам бясконцага парадку. Абазначаецца .

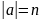Характарыстыка поля – парадак адзінкі ўдачыненні да складання.

Тэарэма 2: Няхай , , тады цыклічная група (a) – канцоўная група парадку n і . (*)

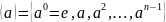Тэарэма 3: Няхай |а|– бясконцага парадку, тады (a) – бясконцая і пры n≠k.

заўвага*: |а|=n тады . У прыватнасці .

Тэарэма 4: Адвольная падгрупа цыклічнай групы цыклічная.

Сцв.2: Няхай . Для адвольнага .

Сцв.3: У цыклічнай групе парадку n, для адвольнага натуральнага дзельніку k, ліку n (k|n) існуе адзіная падгрупа парадку k.

Тэарэма 5: 1) Адвольная бясконцая цыкічная група ізаморфная адытыўнай групе Z;

2) Адвольная канцоўная цыклічная група парадку n ізаморфная групе C(n) камплексных каранёў ступені n з адзінкі.