
- •1. Уравнение Ляпунова для исследования устойчивой линейной системы.
- •2. Переходная матрица. Методы ее нахождения и ее свойства.
- •3. Решение линейной нестационарной системы в пространстве состояний.
- •4. Решение линейной стационарной системы в пространстве состояний.
- •5. Определение управляемости. Анализ управляемости системы.
- •6. Определение наблюдаемости. Анализ наблюдаемости системы.
- •7. Условия управляемости и наблюдаемости Гильберта.
- •8. Метод модального управления.
- •9. Основные свойства нелинейных систем
- •10. Основные типы нелинейностей.
- •11. Понятие фазовой плоскости, фазовой траектории и фазового портрета.
- •18. Вычисление коэффициентов гармонической линеаризации.
- •19. Понятие об эквивалентном комплексном коэффициенте усиления нелинейного элемента.
- •20. Нормированные коэффициенты гармонической линеаризации
- •21. Метод гармонического баланса.
- •22. Определение параметров автоколебаний методом гармонического баланса.
- •23. Критерий устойчивости автоколебаний Попова.
- •24. Анализ автоколебательных режимов с помощью логарифмических частотных характеристик.
- •25. Анализ смещенных автоколебаний.
- •26. Применение метода гармонического баланса для исследования системы, имеющей более одной нелинейной статической характеристики.
- •27. Критерий абсолютной устойчивости Попова.
- •28. Математическое описание процесса преобразования непрерывного сигнала в дискретный сигнал.
- •29. Математическое описание преобразователя дискретного сигнала в непрерывный сигнал.
- •30. Преобразование спектров сигнала при прохождении через импульсный элемент.
- •31. Частотные характеристики экстраполятора нулевого порядка.
- •32. Прохождение сигнала во временной и частотной областях через цепочку элементов а-к, цвм, к-а.
- •33. Передаточная функция и частотные характеристики программы интегрирования, реализованная на цвм методом Эйлера.
- •38. Исследование устойчивости дискретно-непрерывных систем на плоскости s и w*(s).
- •39. Математический аппарат z-преобразования.
- •40. Вычисление z-преобразований сигналов и соответствующих передаточных функций.
- •41. Описание дискретно-непрерывных систем с помощью передаточной функции w(z) и ф(z).
- •42. Построение годографа w(z).
- •43. Анализ устойчивости дискретно-непрерывных систем на плоскости z и w(z)
- •44. Билинейное преобразование. Понятие псевдочастотных характеристик.
- •45. Передаточные функции дискретно-непрерывных систем с экстраполятором нулевого порядка на плоскости w(̄s̄).
- •46. Вычисление переходного процесса в дискретные моменты времени с помощью вычетов.
- •47. Вычисление переходного процесса в дискретные моменты времени с помощью разложения сигнала y(z) в степенной ряд.
- •48. Вычисление переходного процесса в дискретные моменты времени с помощью разложения сигнала y(z)/z на простые дроби.
- •49. Вычисление переходного процесса в дискретные моменты времени с помощью разностного уравнения.
- •50. Построение дискретной модели системы в пространстве переменных состояния.
Пространство переменных состояний:
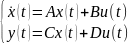
1. Уравнение Ляпунова для исследования устойчивой линейной системы.
Об
устойчивости линейной системы можно
судить, используя уравнение Ляпунова.
Для его вывода мы обозначим функцию
Ляпунова
 .
Эта функция определена в окрестностях
положения равновесия системы, в нуле
она равна нулю. Функция Ляпунова убывает
с течение времени, поэтому
.
Эта функция определена в окрестностях
положения равновесия системы, в нуле
она равна нулю. Функция Ляпунова убывает
с течение времени, поэтому
 ,
вычисляем:
,
вычисляем:
 ,
Q
– положительно определенная матрица
NxN.
Чтобы нулевое решение автономной
линейной системы было асимптотически
устойчивым, необходимо и достаточно,
чтобы для производной положительно
определенной матрицы Q
существовала положительно определенная
матрица P,
удовлетворяющая уравнению Ляпунова.
Уравнение Ляпунова для линейных систем:
,
Q
– положительно определенная матрица
NxN.
Чтобы нулевое решение автономной
линейной системы было асимптотически
устойчивым, необходимо и достаточно,
чтобы для производной положительно
определенной матрицы Q
существовала положительно определенная
матрица P,
удовлетворяющая уравнению Ляпунова.
Уравнение Ляпунова для линейных систем:
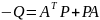 .
Можно доказать, что Q
симметрична
.
Можно доказать, что Q
симметрична
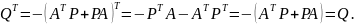 Для
удобства можно брать в качестве Q
единичную матрицу.
Для
удобства можно брать в качестве Q
единичную матрицу.
2. Переходная матрица. Методы ее нахождения и ее свойства.
Переходная
матрица
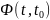 позволяет отыскать решение
позволяет отыскать решение
 в пространстве переменных состояний,
начиная с некоторого значения
в пространстве переменных состояний,
начиная с некоторого значения
 до ∞.
Она должна удовлетворять уравнениям:
до ∞.
Она должна удовлетворять уравнениям:
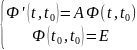 ,
где E
– единичная матрица.
,
где E
– единичная матрица.
Чтобы
отыскать каким образом переходная
матрица связана с
,
будем варьировать векторную переменную
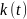 :
:
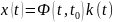
Дифференцируем
систему:
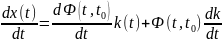 ,
сравниваем с уравнением в пространстве
переменных состояний:
,
сравниваем с уравнением в пространстве
переменных состояний:
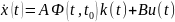
 ,
домножим
на обратную переходную матрицу
,
домножим
на обратную переходную матрицу
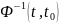 :
:
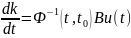
Интегрируем
это выражение:
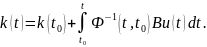 Так как при
Так как при
 выполняется второе уравнение переходной
матрицы, то
выполняется второе уравнение переходной
матрицы, то
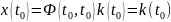 .
Получаем уравнение:
.
Получаем уравнение:
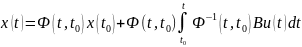 .
Обратная переходная матрица:
.
Обратная переходная матрица:
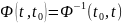 .
Решение системы в общем виде:
.
Решение системы в общем виде:
 ,
где
,
где
 .
Для нахождения переходной матрицы
требуется иметь матрицу
.
Для нахождения переходной матрицы
требуется иметь матрицу
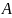 ,
с ее помощью мы находим корни
,
с ее помощью мы находим корни
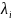 характеристического уравнения
характеристического уравнения
 .
Затем решаем n
уравнений
.
Затем решаем n
уравнений
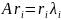 (где n
– порядок системы), откуда узнаем
матрицу
(где n
– порядок системы), откуда узнаем
матрицу
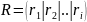 .
.
Переходная
матрица:
 ,
где
,
где
 ,
где
– решения
,
где
– решения
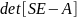 .
.
Второй способ нахождения переходной матрицы:
Для
случая стационарных систем

 ,
,
 .
.
Применим
преобразование Лапласа к диф. уравнению:
 .
Следовательно,
.
Следовательно,
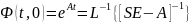
Третий
способ нахождения переходной матрицы:
 ,
где
,
где
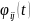 – элемент переходной матрицы, представляет
собой описание переходного процесса
по i-ой
координате вектора состояния при
заданных единичных начальных условиях
на j-ую
координату вектора состояний при
остальных координатах равных нулю.
– элемент переходной матрицы, представляет
собой описание переходного процесса
по i-ой
координате вектора состояния при
заданных единичных начальных условиях
на j-ую
координату вектора состояний при
остальных координатах равных нулю.
Свойства переходной матрицы:
- Переходная матрица полностью определена
- Переходная матрица является невырожденной
3. Решение линейной нестационарной системы в пространстве состояний.
Переходная матрица позволяет отыскать решение в пространстве переменных состояний, начиная с некоторого значения до ∞. Она должна удовлетворять уравнениям:
, где E – единичная матрица.
Чтобы отыскать каким образом переходная матрица связана с , будем варьировать векторную переменную :
Дифференцируем систему: , сравниваем с уравнением в пространстве переменных состояний:
, домножим на обратную переходную матрицу :
Интегрируем это выражение: Так как при выполняется второе уравнение переходной матрицы, то . Получаем уравнение: . Обратная переходная матрица: . Решение системы в общем виде: , где .
