10 ФУНКЦИОНАЛЬНЫЕ РЯДЫ

2 ФУНКЦИОНАЛЬНЫЕ РЯДЫ

2.1 Основные понятия Ряд, членами которого являются функции от переменной х, называется функциональным:

(2.1)

Придавая переменной х определенное значение , получим числовой ряд: , который может быть как сходящимся, так и расходящимся. Если полученный числовой ряд сходится, то точка называется точкой сходимости ряда (2.1); если же ряд расходится – точкой расходимости функционального ряда. Совокупность числовых значений аргумента х, при которых функциональный ряд сходится, называется его областью сходимости. В области сходимости функционального ряда его сумма является некоторой функцией от х: S=S(x). Определяется она в области сходимости равенством , где – частичная сумма ряда. ^ 2.2 Степенные ряды Среди функциональных рядов в математике и ее приложениях особую роль играет ряд, членами которого являются степенные функции аргумента х, т.е. так называемый степенной ряд: (2.2) Действительные (или комплексные) числа называются коэффициентами ряда (2.2), – действительная переменная. Ряд (2.2) разложен по степеням х. Рассматривают также степенной ряд, разложенный по степеням , т.е. ряд вида , (2.3) где – некоторое постоянное число. Ряд (2.3) легко приводится к виду (2.2), если положить . Поэтому при изучении степенных рядов можем ограничиться степенными рядами вида (2. 2). Область сходимости степенного ряда (2.2) содержит по крайней мере одну точку х = 0 (ряд (2.3) сходится в точке ). Теорема 2.1 (Абеля). Если степенной ряд (2.2) сходится при , то он абсолютно сходится при всех значениях х, удовлетворяющих неравенству | х | < ||. Следствие. Если ряд (2.2) расходится при х = , то он расходится и при всех х, удовлетворяющих неравенству |х| > ||. Из теоремы Абеля следует, что если есть точка сходимости степенного ряда, то интервал (-||;|||) весь состоит из точек сходимости данного ряда; при всех значениях х вне этого интервала ряд (2.2) расходится. Интервал (-||;||) называют интервалом сходимости степенного ряда. Положив ||= R, интервал сходимости можно записать в виде (-R; R). Число R называют радиусом сходимости степенного ряда, т. е. 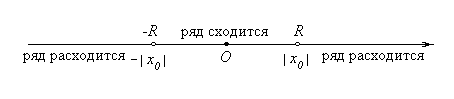радиус сходимости – это такое положительное число R, что при всех х, для которых ||< R, ряд (2.2) абсолютно сходится, а при ||> R – расходится (рисунок 1).

Рисунок 1 – Интервал сходимости степенного ряда

Отметим, что на концах интервала сходимости (т. е. при х = R и при х = -R) сходимость ряда проверяется в каждом случае отдельно. Радиус сходимости степенного ряда (2.2) находится по формулам

,	(2.4)
.	(2.5)

Замечания: 1)  интервал сходимости степенного ряда (2.3) находят из неравенства ||< R; он имеет вид (); 2)  если степенной ряд содержит не все степени х, т.е. задан неполный степенной ряд, то интервал сходимости ряда находят без определения радиуса сходимости (формулы (2.4) и (2.5)), а непосредственно применяя признак Даламбера (или Коши) для ряда, составленного из модулей членов данного ряда. Пример 9. Найти область сходимости ряда. Решение: Воспользуемся формулой (2.4), с учетом, что , : 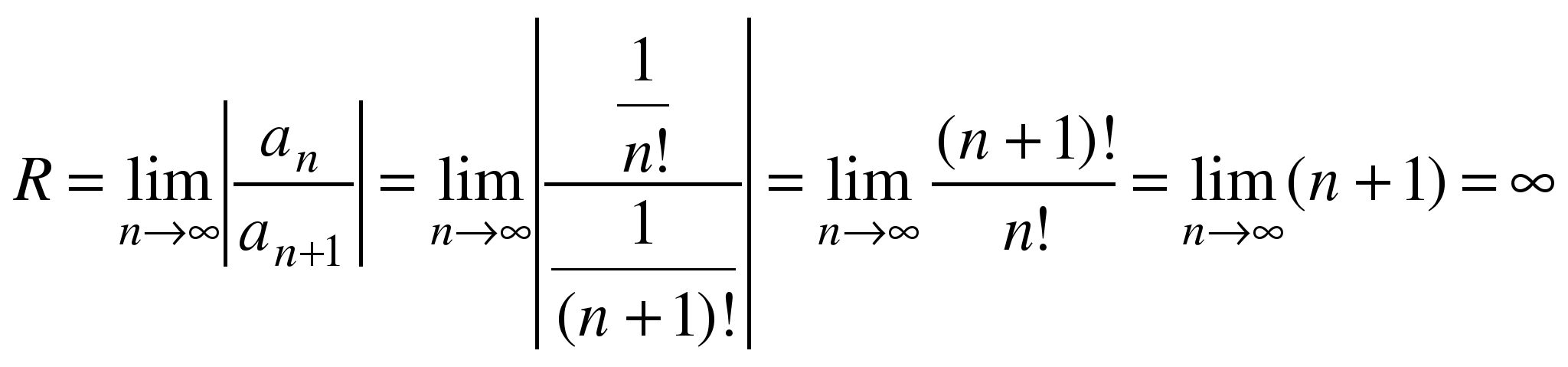. Следовательно, данный ряд абсолютно сходится на всей числовой оси. Пример 10. Найти область сходимости ряда. Решение: Находим радиус сходимости ряда по формуле (2.4). , ; . Следовательно, ряд сходится при , т.е. при . При имеем ряд , который сходится по признаку Лейбница (см. пример 8). При имеем расходящийся ряд . Итак, областью сходимости исходного ряда является промежуток [-4; 0). Пример 11. Найти область сходимости ряда Решение: Заданный ряд неполный. Воспользуемся признаком Даламбера. Для данного ряда имеем: , , . Ряд абсолютно сходится, если < 1 или . Исследуем поведение ряда на концах интервала сходимости. При имеем ряд , который сходится по признаку Лейбница. При имеем ряд – это тоже сходящийся лейбницевский ряд. Следовательно, областью сходимости исходного ряда является отрезок [-1; 1]. Свойства степенных рядов Свойство 1. Сумма S(x) степенного ряда (2.2) является непрерывной функцией в интервале сходимости (-R;R). Свойство 2. Степенные ряды и , имеющие радиусы сходимости R₁ и R₂ соответственно, можно почленно складывать, вычитать и умножать. Свойство 3. Степенной ряд внутри интервала сходимости можно почленно дифференцировать; при этом для ряда при выполняется равенство . Свойство 4. Степенной ряд можно почленно интегрировать на каждом отрезке, расположенном внутри интервала сходимости; при этом для ряда (2.2) при выполняется равенство . Перечисленные свойства 1–4 остаются справедливыми и для степенных рядов вида (2.3).

Равномерная сходимость последовательности функций (отображений) — свойство последовательности , где — произвольное множество, — метрическое пространство, сходится к функции (отображению) , означающее, что для любого существует такой номер , что для всех номеров и всех точек выполняется неравенство

Обычно обозначается .

Это условие равносильно тому, что

[править] Пример

• Последовательность , равномерно сходится на любом отрезке , и не сходится равномерно на отрезке .

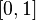[править] Свойства

• Если — линейное нормированное пространство и последовательности отображени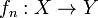й и 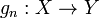, 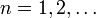равномерно сходятся на множестве 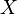, то последовательности 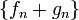также как и 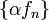при любых 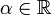также равномерно сходятся на .

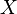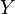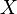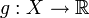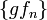• Для вещественнозначных функций (или, более обще, если — линейное нормированное кольцо), последовательность отображений , равномерно сходится на множестве и ограниченное отображение, то последовательность также равномерно сходится на .

• Если 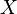— топологическое пространство, — метрическое пространство и последовательность непрерывных в точке 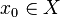отображений 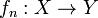равномерно сходится на множестве к отображению 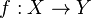, то это отображение также непрерывно в точке .

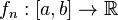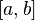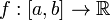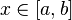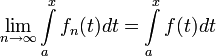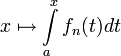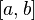• Если последовательность интегрируемых по Риману (по Лебегу) функций равномерно сходится на отрезке к функции , то эта функция также интегрируема по Риману (соответственно по Лебегу), и для любого имеет место равенство      и сходимость последовательности функций      на отрезке к функции 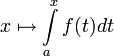     равномерна.

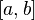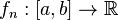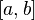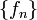• Если последовательность непрерывно дифференцируемых на отрезке функций , сходится в некоторой точке , a последовательность их производных равномерно сходится на , то последовательность также равномерно сходится на 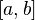, её предел является непрерывно дифференцируемой на этом отрезке функцией.

• ВЕЙЕРШТРАССА ПРИЗНАК

• равномерной сходимости - утверждение, дающее достаточные условия равномерной сходимости ряда или последовательности функций посредством сравнения их с соответствующими числовыми рядами и последовательностями; установлен К. Вейерштрассом [1]. Если для ряда

• 

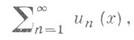
• составленного из действительных или комплексных функций, определенных на нек-ром множестве Е, существует числовой сходящийся ряд

• 

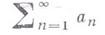
• такой, что

• 

• то исходный ряд сходится равномерно и абсолютно на множестве Е. Напр., ряд

• 

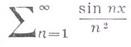
• абсолютно сходится на всей действительной оси, поскольку

• 

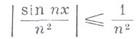
• и ряд

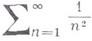• t

• СХОДИТСЯ.

• Если для последовательности действительных или комплексных функций 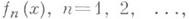сходящейся на множестве к функции 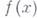, существует бесконечно малая числовая последовательность 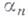такая, что 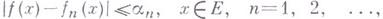то данная последовательность сходится на множестве Еравномерно. Напр., последовательность

• 

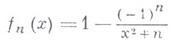
• равномерно на всей действительной оси сходится к функции 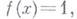так как

• 

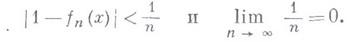
• В. п. равномерной сходимости переносится на функции, значения к-рых лежат в нормированных линейных пространствах.