3. Виды и обозначения напряжений и деформаций. Правило знаков. Закон Гука при растяжении и сдвиге.

Это отношение – среднее напряжение на указанной площадке. При уменьшении размеров площадки (стягивании её в данную точку) в пределе получается напряжение в точке рассматриваемого сечения:

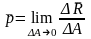
Вектор называют полным напряжением в рассматриваемой точке сечения.

В СИ для измерения напряжений принимается паскаль: 1 Па = 1 Н/м²

Нормальные и касательные напряжения.

Вектор напряжения можно разложить по осям координат на нормальное напряжение , перпендикулярное к сечению, и два касательных напряжения , лежащих в плоскости сечения. Нормальные напряжения препятствуют отрыву одной части элемента от другой или их взаимному прижатию. Касательные напряжения препятствуют взаимному сдвигу.

Формула, связывающая напряжение с продольной силой:

Продольные деформации.

Линейная деформация:

Угловая деформация в точке О в плоскости СОD:

Поперечные деформации.

Закон Гука при растяжении-сжатии.

Напряжения и деформации линейно связаны между собой законом Гука, который подтверждён экспериментально и при растяжении-сжатии стержня имеет вид: , где Е – модуль Юнга.

4. Методы механических испытаний материалов.

Механические испытания – экспериментальное изучение механических св-в материалов на специальных образцах, изготовленных из исследуемого материала.

1) Испытания на растяжение. Осуществляются на специальных разрывных или универсальных машинах. Образец, закреплённый в захватах машины, подвергается принудительному удлинению путём перемещения одного из захватов. Растягивающая сила создаётся испытательными машинами механическим или гидравлическим приводом. Скорость перемещения захватов должна быть постоянной, не более 20 мм/мин. В этом случае нагружение можно считать статическим.

2) Испытания на сжатие. Проводят на специальных прессах или на универсальных машинах и строят диаграммы сжатия. В опытах используют образцы, выполненные в виде коротких цилиндров (высотой 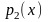, где - диаметр), кубиков и призм.