(положением), и его можно интерпретировать как среднее регио- нальное значение. Остатки Eij являются отклонениями от уравнения
связи двух полей (j-го года и климатического) и характеризуют вну- треннюю неоднородность поля j-го года. Так же как и зависимость (10.28), уравнение (10.40) позволяет разделить все пространствен- ные изменения на две основные части: первую, которая отражает главные показатели пространственных изменений (Y1ij = A1jYсрi + A0j)
и вторую, связанную с внутренней неоднородностью поля (Y2ij = Eij), что так же можно представить в виде обобщенного параметра
– среднего квадратического отклонения остатков – SЕj. Чем больше ве- личина SЕj, тем больше внутренняя неоднородность поля, связанная с локальными особенностями и адвекцией. При SЕj = 0
поле не имеет |
внутренней неоднородности |
и полностью |
соответствует климатиче- скому. Коэффициенты A1j |
и A0j в (10.40) |
|
представлены в отклонениях от среднего климатического поля и при A1j = 1 и A0j = 0 поле j-го года равно среднему многолетнему или
климатическому.
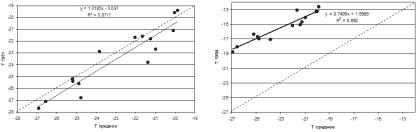
Линейность модели (10.40) постулируется наличием единой функции климатического поля как за каждый год, так и за многолет- ний период, что требует эмпирической проверки. Пример постро- ения ежегодных зависимостей по (10.40) показан на рис. 10.12 для поля температур января на севере Западной Сибири.
Как видно из графиков рис. 10.12, зависимости за отдельные годы являются прямолинейными и достаточно тесными с высокими коэффициентами корреляции R. На этих же графиках пунктиром
Рис. 10.12. Зависимости между климатическим полем температуры января и полями 1951 и 1984 гг. соответственно для 15 метеостанций на севере Западной Сибири
31
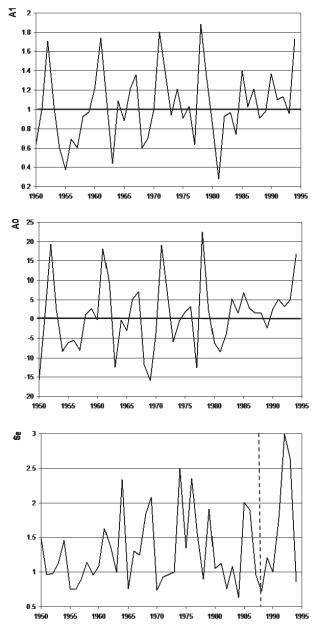
Рис. 10.13. Многолетние ряды коэффициентов A1j, A0j и SЕj пространственной статистической модели температур января на севере Западной Сибири
Следующим большим классом пространственных моделей яв- ляются интерполяционные модели, применяемые для построения изолиний и для получения значений в любой точке пространства на основе интерполяции данных в пунктах наблюдений. В общем случае задача интерполяции сводится к определению значения кли- матической характеристики в любой m-й точке пространства на ос- нове обобщения информации в других точках рассматриваемой тер- ритории. Как правило, это обобщение реализуется в виде
весового осреднения: |
K2Y2 |
2 , 2 . . . KnYn n , n , |
(10.41) |
Ym m , m K1Y1 1, 1 |
где Ym – значение климатической характеристики в любой точке пространства с координатами φm и λm; Y1, Y2, ..., Yn – значения кли-
матической характеристики в пунктах наблюдений с координатами:
φ1, λ1; φ2, λ2; ..., φn, λn; K1, K2, …, Kn, – весовые коэффициенты. Наиболее простым способом является задание весовых коэф-
фициентов обратно пропорциональными расстояниям или квадра- там расстояний до изученного пункта m:
K1 1 / l1 / 1 / l1 1 / l2 1 / ln ;
|
|
|
1 |
K2 |
1 / l2 / |
1 / |
l1 1 / l2 1 / ln , ..., |
|
|||||
|
|
|
|
|
1 |
|
|
1 |
2 |
n |
|
|
|
или |
K |
|
1 / l2 |
/ |
1 / l2 |
1 / l2 |
1 / l 2 |
|
|
||||
|
|
|
K; |
|
1 / l2 |
/ 1 / l2 |
1 / l2 |
1 / l2 |
, |
(10.42) |
|||
|
|
|
2 |
|
|
2 |
|
1 |
2 |
n |
|
||
где l |
, l |
, … l |
– расстояния между неизученным и изученными пун- |
||||||||||
1 |
2 |
n |
|
|
|
|
|
|
|
|
|
|
|
ктами.
Подобный метод интерполяции имеет название метода лучей и в зависимости от топологии пространства (линейное или нелиней-
ное) весовые коэффициенты могут быть даны как в линейной (1/lj ), так и квадратичной (1/l2j) [16].
формеДругим вариантом является использование весовых коэффи- циентов обратно пропорциональными длине перпендикуляров от неизученной точки к линии, соединяющей каждую пару климатиче- ских характеристик на географическом пространстве, как показано на рис. 10.14.
Перпендикуляр представляет собой часть изолинии, проходя- щей через неизученную точку, и чем ближе эта изолиния проходит
33
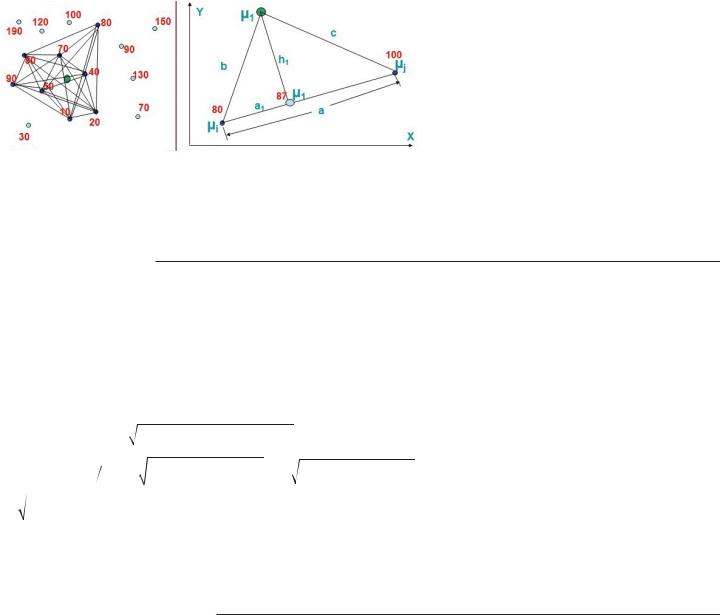
Рис. 10.14. Графическая интерпретация метода перпендикуляров
к рассматриваемой точке, тем больше ее вес. Выражение для полу- чения интерполированного значения в неизученном пункте имеет вид (см. рис. 10.14):
|
cp |
1 / h1 1 1 / h2 2 ... |
(10.43) |
|
|
|
|
|
, |
|
1 / h1 1 / h2 ...
где µср – проинтерполированное значение климатической характе-
ристики в заданной точке пространства; µ1, µ2, … – значения кли-
матической характеристики, полученные на основе линейной ин- терполяции между каждой парой точек с информацией; h1, h2, ... –
расстояния от рассматриваемой точки по перпендикуляру до линии, соединяющей каждую пару пунктов наблюдений.
Каждое значение h вычисляется при этом следующим образом
(см. рис. 10.14 справа): |
p p a p b p c / |
|
(10.44) |
|||
|
h 2 |
|
|
|||
|
|
|
|
|
|
|
где p a b c |
|
|
z i |
|
; |
|
2; a |
j i ; b |
|||||
|
|
|
|
|
2 |
|
|
z j |
|
|
|
2 |
|
2 |
2 |
c |
|
j |
|
i |
||||
, λ , φ , λ , φ , λ , φ , – координаты |
z |
|||||||
(долгота и |
|
|
|
|
|
|
i |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
z |
|
|
|
ji |
i i j j z z |
|
широта) каждой пары пунктов (i и j) и пункта, в который осущест- вляется интерполяция (z).
Каждое проинтерполированное значение (µ) определяется по формуле
Yi a1 ,
(10.45)
где a |
1 |
|
b2 |
h 2 |
; |
= Y – Y при a < a; Y , Y – |
значения климати- |
||
|
|
|
|
|
j i |
1 |
i j |
|
|
ческих характеристик в точках i и j.
Этот метод интерполяции носит название метода перпенди-
куляров, и весовые коэффициенты в нем также могут быть заданы в виде линейной (1/hi ) или квадратичной (1/h2 i) меры.
Исторически имеют место две разновидности интерполяции на географическом пространстве. Первый вид интерполяции связан с построением изолиний и относится к периоду ручной обработки информации и ее интерполяции на географическом пространстве с проведением субъективно сглаженных изолиний. Второй вид ин- терполяции в узлы регулярной сетки развился в условиях
компьютер- |
ной |
интерполяции, когда на |
пространство |
||
накладывается сетка с за- |
данным шагом и данные наблюдений |
||||
интерполируются в |
узлы |
этой |
сетки [19]. |
Таким образом |
|
сформированы, например, климатические архивы данных реанализа для сеточных климатических моделей.
Приведенные здесь методы интерполяции: метод лучей и метод перпендикуляров позволяют осуществлять оперативную интерпо- ляцию в любую точку пространства, при этом можно выбрать оп- тимальное число точек, по которым осуществляется интерполяция путем сравнения интерполированных и наблюденных данных. Для этой цели ближайшие к рассматриваемой неизученной точке пункты наблюдений последовательно переводятся в категорию «неизучен- ных» и в них проводится интерполяция при разном
наборе пунктов |
с данными наблюдений. Затем значение, |
|
полученное с |
помощью |
интерполяции, сравнивается с |
фактическим и рассчитывается «не- зависимая» погрешность, то есть на независимом от расчета мате- риале наблюдений. При этом можно варьировать набором пунктов для интерполяции, методом и
линейностью |
весовых коэффициен- |
тов для |
достижения |
минимальной |
погрешности. Условия, при |
кото- рых получена |
|
минимальная погрешность, и будут оптимальными на |
практике с |
||
точки зрения выбираемых для интерполяции пунктов и топологии пространства.
10.4.Статистические модели от факторов
ианализ остатков
Часто бывает необходимо построить статистическую модель от факторов, формирующих рассматриваемую характеристику и на
нее влияющих вида: Y = f(X , X , …, X ), где Y – отклик; X , X , …,
Xm – факторы. Примеры этих моделей могут быть разнообразные:
от построения региональных зависимостей температуры или осадков от высоты местности и других азональных факторов до построе- ния уравнений, связывающих между собой коэффициенты и пара- метры различных статистических моделей. Для построения таких зависимостей от факторов применяются регрессионный анализ и уравнение множественной или, в частном случае, одного фактора – простой регрессии. Как правило, применяется линейный регресси- онный анализ, когда любые непрямолинейные зависимости отклика от факторов могут быть сведены к прямолинейным за счет функ- циональных преобразований, например, Z = lg(X), Z = eX, Z = X2 и других.
Построение статистических регрессионных зависимостей от факторов включает три стадии [9].
1. Предварительный анализ данных для: а) выбора предпола- гаемых факторов; б) построения и анализа однофакторных зависи- мостей с целью оценки тесноты связи с рассматриваемым фактором и необходимости функциональных преобразований.
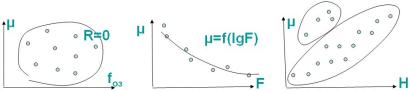
Выбор предполагаемых факторов основан не только на оценке тесноты связи, но и на анализе разброса точек в однофакторной за- висимости на предмет оценки «лишних точек», отклоняющихся от общей взаимосвязи и поиска причин, которые их обусловили. При- меры анализа однофакторных зависимостей показаны на рис. 10.15. Первый график свидетельствует о том, что зависимость отклика μ
от фактора fоз отсутствует, так как коэффициент корреляции R = 0. Но это не означает, что фактор fоз должен быть сразу исключен из уравнения, – его можно оставить, но только при оценке совместных эффектов, то есть произведения этого фактора с другим. Фактор мо- жет быть и не связан с откликом напрямую, но произведение
Рис. 10.15. Примеры анализа однофакторных зависимостей отклика μ от факторов fоз, F, Н
36
На среднем графике (см. рис. 10.15) показана не прямолиней- ная зависимость μ от F, которая свидетельствует о необходимости выполнить функциональное преобразование и представить этот фактор, например как lg(F). Последний правый график свидетель- ствует о том, что в зависимости μ от Н в ее верхней части есть «лиш- ние» точки, которые уменьшают тесноту связанности и находятся с краю от нее. Поэтому эти отклоняющиеся от зависимости точки надо проанализировать и установить причины их отклонений. На- пример, одной из причин может быть их расположение на границе района, и поэтому они уже могут не принадлежать рассматривае- мому однородному району, границы которого требуется скорректи- ровать и уменьшить, а затем построение и анализ однофакторных зависимостей повторить.
2. Вторая стадия моделирования связана: а) с формированием общей структуры региональной зависимости; б) определением ко- эффициентов регрессионной зависимости с учетом их статистиче- ской значимости.
Общая структура уравнения множественной регрессии может быть задана или аналитически, в соответствии со структурой из- вестного применяемого уравнения, например, теплового баланса, или подобрана эмпирически из нескольких основных структур:
–аддитивная структура без функциональных преобразований,
когда факторы не зависят один от другого: |
|
Y b1 X1 b2 X 2 b0 , |
(10.46) где b1, |
b2, …, b0 – коэффициенты уравнения, вычисляемые по МНК;
– аддитивная структура с функциональными преобразования- ми факторов:
Y b1 lg X1 b2 X 22 b0 ;
(10.47)
–мультипликативная структура, включающая произведения факторов (совместные эффекты):
Y b1 X1·X 2 b2 X 2·X 3 b0 ;
(10.48)
–комплексная, или смешанная, структура, включающая адди- тивные факторы, функциональные преобразования и совместные эффекты:
Y b1X1 b2 X 22 b3 X1X 2 b4 X 2 X 3 b5 X1·lg X 4 b0.
значимости, например с помощь 95 %-ного или 2σ-го доверительно интервала случайной погрешности коэффициентов. Если факторы и структура уравнения являются нелинейными и не могут быть ли- неаризованы, то для расчета коэффициентов таких уравнений при- меняются методы нелинейного МНК: симплекс-метод, метод Розен-
брока, метод креста и т.д. в зависимости от сложности поверхности коэффициентов [16].
Для оптимизации вычислений уравнений сложной структу- ры применяют также методы получения эффективного по составу факторов уравнения. Для выбора такого «наилучшего» уравнения регрессии обычно применяется два известных метода: метод ис- ключения и шаговая процедура, или метод включения [5].
Метод исключения представляет собой усовершенствованный вариант метода «всех регрессий», то есть полного перебора всех возможных сочетаний факторов. Основные этапы метода исключе- ния следующие:
–рассчитывается регрессионное уравнение, включающее все переменные;
–рассчитывается величина частного F-критерия для каждой из переменных, как будто бы она была последней переменной, введен- ной в регрессионное уравнение;
–наименьшая величина частного F-критерия, обозначенная, например, через FL, сравнивается с заранее выбранным уровнем значимости F0 и
–если FL < F0, то переменная XL, связанная с FL, исключает- ся
из рассмотрения и производится пересчет уравнения регрессии с учетом оставшихся переменных и затем осуществляется переход ко второму шагу и анализируется следующая переменная на пред- мет исключения из уравнения и т.д.;
–если FL > F0, то регрессионное уравнение оставляют таким,
как оно было получено.
В результате применения этого метода в уравнении остаются только те факторы, исключение каждого из которых приводит к ста- тистически значимому уменьшению дисперсии, объясненной с по- мощью уравнения.
Второй метод – шаговая процедура является улучшенным вари- антом метода включения и содержит следующие шаги.
Шаг 1. Шаговый метод начинается с построения простой корре- ляционной матрицы и включения в регрессионное уравнение пере- менной X, наиболее сильно коррелированной с откликом (например, X1), то есть с наибольшим коэффициентом
Шаг 2. Выбирается следующая переменная (X2), у которой
коэффициент парной корреляции тоже большой, но меньший, чем
у X1.
Шаг 3. Получают регрессионное уравнение с двумя перемен- ными: Y = f(X1, X2) и затем исследуют вклад переменной X1, кото-
рый имел бы место, если бы в модель была введена сначала X2, а затем X1, и если этот вклад статистически значимо увеличивает
объясненную уравнением долю неопределенности, то переменную X1 оставляют в уравнении.
Шаг 4. Далее включают следующую по величине парно- го коэффициента корреляции переменную X3 и строят уравнение: Y =
f(X1, X2, X3) и затем в него вначале включают переменную X3, а затем последовательно X1 и X2, при этом оценивая, увеличивается
эффективность уравнения с включением каждой новой переменной или нет и если нет, то переменную не включают.
Шаг 5 и остальные. Процесс продолжается до тех пор, пока не будут рассмотрены все переменные.
Помимо этих двух методов раньше применялся также и
ступен- чатый регрессионный метод, имеющий простую графическую ин- терпретацию. В этом методе также, как и в шаговой процедуре вна- чале строится однофакторное уравнение с переменной, имеющей
наиболее высокий коэффициент парной корреляции Y = f(X1). Затем находятся разности между фактическими Yi и
рассчитанными по
этому уравнению Y’i, то есть остатки Zi = Yi – Y’i. Эти остатки теперь
рассматриваются как значения нового отклика и строится регресси- онная зависимость этого нового отклика со следующим фактором, имеющих наибольшее значение коэффициента парной корреляции. Этот процесс продолжается до любой конечной стадии, например, до тех пор, пока значение коэффициента парной корреляции станет статистически незначимым.
3. Третья, последняя, стадия моделирования связана с оценкой эффективности построенных региональных зависимостей и имеет самостоятельное название – анализ остатков [5].
Остатки любой эмпирической зависимости определяются как разности между фактическими (наблюденными) и расчетными по этой зависимости значениями:
В качестве безразмерной характеристики остатков могут рас-
сматриваться их относительные значения (Δi): |
|
i Yi Yi Yi , |
(10.51) |
которые выражаются в долях единицы или процентах. Наиболее распространенной обобщенной характеристикой
остатков является их среднее квадратическое отклонение (σε):
n2
|
i |
, |
(10.52) |
|
|
||||
|
i 1 |
n 1 |
|
|
или |
|
|
|
|
|
|
1 |
|
(10.53) |
|
|
|||
|
Y |
|
|
|
R2 ,
где ¯ε– среднее значение остатков; R – коэффициент корреляции по- лученной зависимости; σY – стандартное (среднее квадратическое)
отклонение ряда фактических значений.
Стандартная погрешность дает первичную информацию об эф- фективности полученной эмпирической зависимости. В качестве
обобщенной меры может служить также величина:
(10.54)
1 R2 ·100
которая характеризует долю исходного рассеивания (в %), не объяс- %,
ненного с помощью построенной зависимости.
Стандартная погрешность остатков, как следует из (10.53) и (10.54), связана с коэффициентом корреляции полученного уравнения. Поэтому можно решать и обратную задачу: определить,
каким должен |
быть коэффициент |
корреляции, чтобы уравнение |
||||
удовлетворяло |
прак- |
тической |
эффективности, |
например, по |
||
заданной |
стандартной |
по- |
грешности |
климатической |
||
характеристики, |
вычисляемой по |
уравне- |
нию |
(10.53). Если |
||
полученное уравнение имеет эффективность ниже, чем требуемая, то
его можно |
попытаться улучшать путем введения |
новых факторов, |
|
изменения |
структуры зависимости |
и т. д. При этом необходимо |
|
иметь в виду, что практическая |
эффективность |
должна быть |
|
ориентирована на реальные возможности, связанные с погреш- ностями измерений и пространственно-временных обобщений факто- ров и определяемой климатической характеристики, с ограниченно- стью объема данных, множеством неучтенных факторов и т. д.