12. Интервальная оценка мат. Ожидания нормально распределенного признака при известном среднем квадратическом отклонении.
Интервальной называют оценку, которая определяется двумя числами – концами интервала, покрывающего оцениваемый параметр.
Доверительным называют
интервал, который с заданной
надежностью 
покрывает
заданный параметр.
1. Интервальной
оценкой (с надежностью 
)
математического ожидания 
нормально
распределенного количественного
признака 
по
выборочной средней при
известном среднем квадратическом
отклонении 
генеральной
совокупности служит доверительный
интервал
,
(18)
где 
–
точность оценки;
–
объем выборки;
–
значение аргумента
функции Лапласа 
,
при котором 
;
при неизвестном 
(и
объеме выборки 
)
,
(19)
где 
–
«исправленное» выборочное среднее
квадратическое отклонение, 
находят
по таблице приложения 3 по заданным 
и 
.
2. Интервальной
оценкой (с надежностью 
)
среднего квадратичекого отклонения 
нормально
распределенного количественного
признака 
по
«исправленному» выборочному среднему
квадратическому отклонению 
служит
доверительный интервал
(20)
где 
находят
по таблице приложения 4 с заданными 
и 
.
3. Интервальной
оценкой (с надежностью 
)
неизвестной вероятности 
биноминального
распределения по
относительной частоте 
служит
доверительный интервал (с приближенными
концами 
и 
)
,
где 
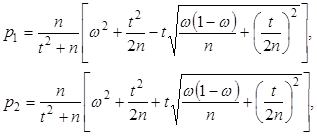(21)
где 
–
общее число испытаний; 
–
число появлений события; 
–
относительная частота, равная
отношению 
; 
–
значение аргумента функции Лапласа
(приложение 2), при котором 
( 
–
заданная надежность).
Замечание. При
больших значениях 
(порядка
сотен) можно принять в качестве
приближенных границ доверительного
интервала
, 
.
(22)
Пример.
Найти доверительный интервал для оценки
с надежностью 0,975 неизвестного
математического ожидания 
нормально
распределенного признака 
генеральной
совокупности, если генеральное среднее
квадратическое отклонение 
,
выборочная средняя 
и
объем выборки 
.
Решение. Требуется найти доверительный интервал
.
(23)
Все величины,
кроме 
,
известны. Найдем 
из
соотношения . По таблице
приложения 1 находим 
.
Подставив 
, 
, 
, 
в
(23), окончательно получим искомый
доверительный интервал 
.
Пример.
Найти минимальный объем выборки, при
котором с надежностью 0,95 точность оценки
математического ожидания 
генеральной
совокупности по выборочной средней
равна 
,
если известно среднее квадратическое
отклонение 
нормально
распределенной генеральной совокупности.
Решение. Воспользуемся
формулой, определяющей точность оценки
математического ожидания генеральной
совокупности по выборочной средней: 
.
Отсюда 
.
(24)
по условию, 
;
следовательно, 
.
По таблице приложения 2 найдем 
.
Подставив 
, 
и 
в
(24), получим искомый объем выборки 
.
Пример.
Произведено 15 измерений одним прибором
(без систематической ошибки) некоторой
физической величины, причем «исправленное»
среднее квадратическое отклонение 
случайных
ошибок измерений оказалось равным 0,7.
Найти точность прибора с надежностью
0,99. Предполагается, что результаты
измерений распределены нормально.
Решение. Точность
прибора характеризуется средним
квадратическом отклонением случайных
ошибок измерений. Поэтому задача сводится
к отысканию доверительного интервала,
покрывающего 
с
заданной надежностью 
:
.
(25)
По данным 
и 
по
таблице приложения 4 найдем 
.
Подставив 
, 
в
соотношение (25), окончательно получим 
.