4. Зависимые и независимые случайные величины. Ковариация и коэффициент корреляции случайных величин. Связь между некоррелированностью и независимостью случайных величин.

Случайные величины называются независимыми, если закон распределения одной из них не зависит от того какое значение принимает другая случайная величина.

Условные распределения независимых случайных величин равны их безусловным распределениям.

Теорема. Для того, чтобы случайные величины Х и Y были независимы, необходимо и достаточно, чтобы функция распределения системы (X, Y) была равна произведению функций распределения составляющих.

Аналогичную теорему можно сформулировать и для плотности распределения:

Теорема. Для того, чтобы случайные величины Х и Y были независимы, необходимо и достаточно, чтобы плотность совместного распределения системы (X, Y) была равна произведению плотностей распределения составляющих.

Пусть имеется двумерная СВ (Х,Y), распределение которой известно, т.е. известна табл. 5.1 или совместная плотность вероятности . Тогда можно найти математические ожидания М(Х) = а_х, М(Y) = а_у и дисперсии иодномерных составляющих Х иY. Однако математические ожидания и дисперсии случайных величин Х и Y недостаточно полно характеризуют двумерную случайную величину (Х,Y), т.к. не выражают степени зависимости ее составляющих Х и Y эту роль выполняют ковариация и коэффициент корреляции.

Определение. Ковариацией (или корреляционным моментом) К_ху случайных величин Х и Y называется математическое ожидание произведения отклонений этих величин от своих математических ожиданий, т.е.

, Или ,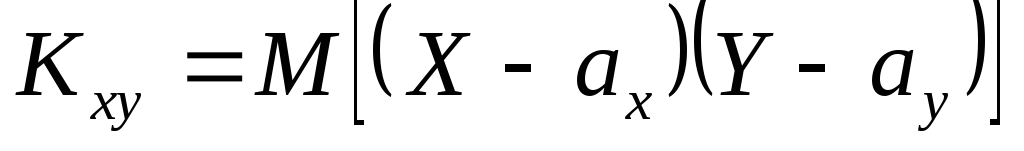

Где ,.

Из определения следует, что . Кроме того,.

т.е. ковариация СВ с самой собой есть ее дисперсия.

Для дискретных случайных величин:

 .

Для непрерывных случайных величин:

 .

Ковариация двух случайных величин характеризует как степень зависимости случайных величин, так и их рассеяние вокруг точки . Об этом, в частности, свидетельствуютсвойства ковариации случайных величин.

1. Ковариация двух независимых случайных величин равна нулю.

2. Ковариация двух случайных величин равна математическому ожиданию их произведения минус произведение математических ожиданий, т.е. , или.

3. Ковариация двух случайных величин по абсолютной величине не превосходит произведения их средних квадратических отклонений, т.е..

Ковариация, как уже отмечено, характеризует не только степень зависимости двух случайных величин, но и их разброс, рассеяние. Кроме того, она - величина размерная, ее размерность определяется произведением размерностей случайных величин. Это затрудняет использование ковариации для оценки степени зависимости для различных случайных величин. Этих недостатков лишен коэффициент корреляции.

Определение. Коэффициентом корреляции двух случайных величин называется отношение их ковариации к произведению средних квадратических отклонений этих величин:

.

Из определения следует, что . Очевидно также, что коэффициент корреляции естьбезразмерная величина.

Свойства коэффициента корреляции:

1. Коэффициент корреляции принимает значения на отрезке [-1;1], т.е. .

2. Если случайные величины независимы, то их коэффициент корреляции равен нулю, т.е. .

Случайные величины называются некоррелированными, если их коэффициент корреляции равен нулю. Т.о., из независимости случайных величин следует их некоррелированность. Обратное утверждение, вообще говоря, неверно: из некоррелированности двух случайных величин еще не следует их независимость.

3. Если коэффициент корреляции двух случайных величин равен (по абсолютной величине) единице, то между этими случайными величинами существует линейная функциональная зависимость.

Закон распределения дискретной с.в.задан таблицей

	-1	0	1
0
1

Найти коэффициент корреляции 

Решение. Находим законы распределения составляющихи:

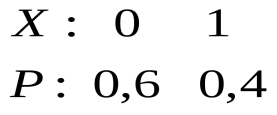
Теперь вычислим м.о. составляющих:

.

Этих величин можно было находить на основании таблицы распределения с.в. 

из равенства (1) пункта 12.1. Например,

.

Аналогично, находите самостоятельно.

Вычислим дисперсии составляющих при это будем пользоваться вычислительной формулой:

Следовательно,Далее, на основании первой формулы

(6) имеем:

Составим закон распределения , а затем найдём:

При составлении таблицы закона распределения следует выполнять действия:

1) оставить лишь различные значения всевозможных произведений .

2) для определения вероятности данного значения , нужно

складывать все соответствующие вероятности, находящиеся на пересечении основной таблицы, благоприятствующие наступлению данного значения.

В нашем примере с.в.принимает всего три различных значения. Здесь первое значение () соответствует произведениюиз второй строки ииз первого столбца, поэтому на их пересечении находится вероятностное числоаналогично

,

которое получено из суммы вероятностей, находящихся на пересечениях соответственно первой строки и первого столбца (0,15 ; 0,40; 0,05) и одно значение , которое находится на пересечении второй строки и второго столбца, и наконец,, которое находится на пересечении второй строки и третьего столбца.

Из нашей таблицы находим:

Находим корреляционный момент, используя формулу (38):

Находим коэффициент корреляции по формуле (41)

Таким образом, отрицательная корреляция.