
Волны и квантовая физика Разное
-
Градусы Цельсия и кельвина – связь T(K)=t(°C) + 273
З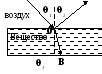 аконы
преломления и отражения
Закон
отражения: Θ1= Θ2
аконы
преломления и отражения
Закон
отражения: Θ1= Θ2
Закон
преломления:
![]()
-
Интенсивность и амплитуда волны I ~ A2
-
Длинна волны, частота и циклическая частота колебаний в волне, волновое число
-
ω – циклическая частота колебаний в волне (рад/с)
-
ν или f – частота колебаний в волне (с-1=Гц). ν = ω /2π
-
T – период колебаний (с). T = 1/ ν = 2π/ω
-
v – скорость распространения волны (фазовая скорость)
-
λ – длина волны (м). λ=vT=v/ ν
-
k – волновое число (м-1). k = 2π/ λ
-
Электрон-вольт 1эВ = 1.602·10-19Дж
Интерференция
-
Оптическая длина пути L = n·l Пример: Н
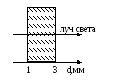 айти
оптическую длину пути в прозрачной
пластинке с показателем преломления
n= 1,43(в мм).
айти
оптическую длину пути в прозрачной
пластинке с показателем преломления
n= 1,43(в мм).
-
Оптическая разность ходжа в плоскопараллельной пластине Пример: Оптическая разность хода лучей 1 и 2 ( ОВ=ВС= 5 мм, ОА= 0,1 мм) равна (в мм).
-
У
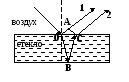 словие
минимума и максимума при интерференции
двух лучей (через оптическую разность
хода)
max: Δ=mλ
min:
Δ=(m+1/2) λ
Пример:
В точке А оптическая
разность хода когерентных лучей 1 и 2
равна Δ= 0,75 мкм. Для какой длины волны
будет наблюдаться интерференционный
минимум с m=0 (в
мкм).
Оптическая разность хода лучей
1 и 2 равна Δ=1,35 мкм. Для какой длины
волны будет наблюдаться интерференционный
максимум с m=3.
словие
минимума и максимума при интерференции
двух лучей (через оптическую разность
хода)
max: Δ=mλ
min:
Δ=(m+1/2) λ
Пример:
В точке А оптическая
разность хода когерентных лучей 1 и 2
равна Δ= 0,75 мкм. Для какой длины волны
будет наблюдаться интерференционный
минимум с m=0 (в
мкм).
Оптическая разность хода лучей
1 и 2 равна Δ=1,35 мкм. Для какой длины
волны будет наблюдаться интерференционный
максимум с m=3.
-
Максимальная и минимальная амплитуда при сложении когерентных волн Пример: Амплитуды колебаний ( в условных единицах) от двух когерентных источников света равны А1= 10 и А2= 30. Какую максимальную и минимальную амплитуды будет иметь суммарное колебание.
Дифракция
-
Дифракционный максимум решетки max: d·sin(φmax) = m·λ Пример: На дифракционную решетку с постоянной d= 20 мкм падает свет с длиной волны λ=0,74мкм. Под каким углом виден дифракционный максимум второго порядка.
-
С
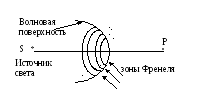 уммарная
амплитуда при сложении колебаний от
зон Френеля.
Пример:
В условных
единицах в т.Р амплитуды колебаний от
первых четырех зон Френеля соответственно
равны: А1= 5 А2= 4 А3= 3
А4= 2. Если открыты зоны все четыре,
то результирующая амплитуда в т. Р
равна:
уммарная
амплитуда при сложении колебаний от
зон Френеля.
Пример:
В условных
единицах в т.Р амплитуды колебаний от
первых четырех зон Френеля соответственно
равны: А1= 5 А2= 4 А3= 3
А4= 2. Если открыты зоны все четыре,
то результирующая амплитуда в т. Р
равна:
-
Условие минимумов и максимумов при дифракции на щели min: a·sin(φmin) = mλ max: a·sin(φmin) = (m+1/2)λ Пример: Чему равен порядок дифракционного минимума от света с длиной волны λ=0,7мкм, падающего под углом φ=30о на щель шириной а =2,8 мкм? Свет с длиной волны λ = 0,7 мкм, падающий на щель, дает дифракционный максимум третьего порядка под углом φ=30о. Найти ширину щели(в мкм).
-
Постоянная (период) дифракционной решетки Пример: В дифракционной решетке, имеющей N= 150 штрихов на миллиметр, ширина непрозрачных участков b= 0.1мкм. Чему равна ширина прозрачных участков этой решетки (в мкм).
-
Условие минимумов и максимумов при дифракции рентгеновских лучей на одномерной кристаллической решетке. max: 2dsin(φ) = mλ Пример: Рентгеновские лучи с длиной волны 0,2 нм дают дифракционный максимум первого порядка на кристаллической решетке с периодом d= 0,25 нм при угле скольжения (в градусах).
