Сложность алгоритма

Сложность – это способ сравнения алгоритмов. Их сравнивают по количеству необходимых для выполнения алгоритма шагов (временная сложность) и по объему памяти, необходимой для работы алгоритма (емкостная сложность).

Все задачи по сложности можно разделить на три класса:

– класс полиномиальной сложности P,

– класс экспоненциальной сложности,

– класс NP.

Класс P относят к легкорешаемым задачам, класс экспоненциальной сложности – к труднорешаемым задачам. По этой классификации сложность легкорешаемых задач не превосходит некоторый полином P от размерности задачи. Сложность труднорешаемых задач превосходит любой полином от n (сложность труднорешаемых задач имеет экспоненциальный рост от n). Класс NP объединяет задачи, которые не отнесены ни к легкорешаемым, ни к труднорешаемым задачам.

Некоторые задачи вместо решения лишь сводятся одна к другой алгоритмом полиномиальной сложности. Они составляют класс задач, эквивалентных по сложности.

Задачи неизвестной сложности, но эквивалентные по сложности, называются NP-полными.

Рассмотрим для иллюстрации таблицу, содержащую четыре столбца, соответствующие «абстрактному» объему исходных данных (n).

Строки соответствуют различным значениям функции сложности вычислений F, в зависимости от объема данных и сложности вычислений.

n F	10	30	50	60
n	10–5 cек.	cек.	cек.	cек.
n5	0,1 cек.	24,3 cек.	5,2 мин.	13 мин.
2n	10–3 cек.	17,9 мин.	35,7 лет	366 столетий

С точки зрения теории сложности вычислений, первые две задачи относятся к классу задач с полиномиальной сложностью, а последняя – к задачам с экспоненциальной сложностью.

Введение сложностной характеристики алгоритма приводит к двум направлениям исследования: во-первых, поиск алгоритма решения для легкорешаемых задач; во-вторых, проверка задачи на труднорешаемость или NP-полноту.

То есть все задачи можно разделить на 4 типа:

1. алгоритмически неразрешимые;

2. алгоритмически разрешимые с экспоненциальной сложностью;

3. NP-полные;

4. алгоритмически разрешимые с полиномиальной сложностью.

Примером алгоритмически неразрешимых задач является проблема распознавания выводимости в математической логике (существует ли алгоритм логического вывода из формулы A формулы B для любых двух формул A и B).

Есть какая-то аналогия между проблемами алгоритмической разрешимости и трудноразрешимости. Как из-за невозможности определить понятие алгоритма проблема алгоритмической разрешимости сводится к возможности построения конкретизации, так и трудноразрешимость устанавливается сведением исследуемой задачи к одной из «эталонных» NP-полных задач.

6.3. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ АЛГОРИТМОВ

При решении практических задач, предполагающих разработку алгоритмов для реализации на ЭВМ, и тем более при использовании на практике информационных технологий алгоритмизация выступает как набор определенных практических приемов, особых специфических навыков рациональ­ного мышления в рамках заданных языковых средств.

Остановимся на графическом описании алгоритма, называемом блок-схемой. Этот способ имеет ряд преимуществ благодаря наглядно­сти, обеспечивающей, в частности, высокую «читаемость» алгоритма и явное отображение управления в нем.

Прежде всего определим понятие блок-схемы. Блок-схема - это ориентирован­ный граф, указывающий порядок исполнения команд алгоритма; вершины такого графа могут быть одного из трех типов (рис. 1.12)

Базовые алгоритмические структуры

"Алгоритм" является базовым основополагающим понятием информатики, а алгоритмизация (программирование) – основным разделом курса информатики (ядром курса). Понятие алгоритма, как и понятие информации, точно определить невозможно. Поэтому встречаются самые разнообразные определения – от "наивно-интуитивных" ("алгоритм – это план решения задачи") до "строго формализованных" (нормальные алгоритмы Маркова).

В качестве рабочего определения алгоритма возьмем следующее определение.

Алгоритм – это упорядоченная совокупность точных (формализованных) и полных команд исполнителю алгоритма (человек, ЭВМ), задающих порядок и содержание действий, которые он должен выполнить для нахождения решения любой задачи из рассматриваемого класса задач.

Алгоритм удовлетворяет следующим основным свойствам алгоритмов:

9. Конечность (дискретность) команд и выполняемых по ним действий алгоритма.

10. Выполнимость в определенной операционной среде (в определенном классе исполнителей).

11. Результативность отдельных команд и всего алгоритма.

12. Применимость алгоритма ко всем возможным входным данным конкретного класса задач.

13. Определенность (детерминированность) команд и всего алгоритма для всех входных данных.

14. Формализованное, конструктивное описание (представление) команд алгоритма.

15. Минимальная полнота системы команд алгоритм.

16. Непротиворечивость любых команд алгоритма на любом наборе входных данных.

Любой алгоритм ориентирован на некоторый общий метод решения класса задач и представляет собой формализованную запись метода, процедуры.

Алгоритм, записанный на некотором алгоритмическом, формальном языке, состоит из заголовка алгоритма (описания параметров, спецификаций класса задач) и тела алгоритма (последовательности команд исполнителя, преобразующих входные параметры в выходные).

Для записи, исполнения, обмена и хранения алгоритмов существуют различные средства, языки, псевдокоды – блок-схемы, структурограммы (схемы Нэсси-Шнайдермана), Р-схемы, школьный алгоритмический язык (ШАЯ), различные языки программирования.

Различают три базовые алгоритмические структуры: следование, ветвление, повторение.

1. Структура следование состоит из двух команд с указанной очередностью их выполнения и имеет вид:

2. <команда – предшественник>;

3. <команда – преемник>.

4. Структура типа ветвления в полной форме состоит из некоторого условия, проверяемого на истинность при выполнении структуры, команды, выполняемой при выполнении проверяемого условия, и команды, выполняемой при невыполнении условия. Структура имеет вид

5. if <условие>

6. then <команда, выполняемая при выполнении условия>

7. else <команда, выполняемая при невыполнении условия>;.

Ключевые (служебные) слова Паскаля – if (если), then (то), else (иначе). Ключевые слова нельзя изменять, заменять, так как их эталоны закреплены в переводчике с языка Паскаль (о нем подробнее – ниже).

Пример. Команда вида

if (х>y) { если текущее значение х больше текущего значения y, }

then у := х { то текущее значение у полагаем равным текущему значению х, }

else x:= y; { иначе (при х <= y) текущее значение x заменяем на текущее значение y }.

Структура типа ветвления в неполной форме – частный случай ветвления в полной форме, в которой, при невыполнении условия, управление просто передается следующей команде и больше никаких действий команда ветвления не осуществляет. Эта структура имеет вид

if <условие>

then <команда, выполняемая при исполнении условия>; .

Структура повторения (цикл) служит для компактной записи одного и того же набора команд, повторяемых для различных значений параметров команд.

Структура повторения типа "пока (while)" записывается в виде:

while <условие продолжения повторения> do

<повторяемая команда>;

или

while <условие продолжения повторения> do

begin

<повторяемая команда номер 1>;

<повторяемая команда номер 2>;

. . .

<повторяемая команда номер N>

end;.

Ключевые слова Паскаля – while (пока), do (выполнять), begin (начало), end (конец).

Телом цикла называется последовательность повторяемых команд, которая может быть и пустой (редко встречаемый случай).

Часть команды цикла "while <условие продолжения повторения>" – заголовок цикла.

Данный цикл выполняется по правилу: если условие повторения для текущих его параметров не выполнено, то повторение команд (тела) цикла на этом завершается; если же оно выполнено, то выполняется тело цикла и опять проверяется условие повторения команд тела цикла.

1. Лекция: Методы разработки и анализа алгоритмов

Нисходящим проектированием алгоритмов, проектированием алгоритмов "сверху вниз" или методом последовательной (пошаговой) нисходящей разработки алгоритмов называется такой метод составления алгоритмов, когда исходная задача (алгоритм) разбивается на ряд вспомогательных подзадач (подалгоритмов), формулируемых и решаемых в терминах более простых и элементарных операций (процедур). Последние, в свою очередь, вновь разбиваются на более простые и элементарные, и так до тех пор, пока не дойдём до команд исполнителя. В терминах этих команд можно представить и выполнить полученные на последнем шаге разбиений подалгоритмы (команд системы команд исполнителя).

Восходящий метод , наоборот, опираясь на некоторый, заранее определяемый корректный набор подалгоритмов, строит функционально завершенные подзадачи более общего назначения, от них переходит к более общим, и так далее, до тех пор, пока не дойдем до уровня, на котором можно записать решение поставленной задачи. Этот метод известен как метод проектирования "снизу вверх".

Структурные принципы алгоритмизации (структурные методы алгоритмизации) – это принципы формирования алгоритмов из базовых структурных алгоритмических единиц (следование, ветвление, повторение), используя их последовательное соединение или вложение друг в друга с соблюдением определённых правил, гарантирующих читабельность и исполняемость алгоритма сверху вниз и последовательно.

Структурированный алгоритм – это алгоритм, представленный как следования и вложения базовых алгоритмических структур. У структурированного алгоритма статическое состояние (до актуализации алгоритма) и динамическое состояние (после актуализации) имеют одинаковую логическую структуру, которая прослеживается сверху вниз ("как читается, так и исполняется"). При структурированной разработке алгоритмов правильность алгоритма можно проследить на каждом этапе его построения и выполнения.

Теорема (о структурировании). Любой алгоритм может быть эквивалентно представлен структурированным алгоритмом, состоящим из базовых алгоритмических структур.

Одним из широко используемых методов проектирования и разработки алгоритмов (программ) является модульный метод (модульная технология).

Модуль – это некоторый алгоритм или некоторый его блок, имеющий конкретное наименование, по которому его можно выделить и актуализировать. Иногда модуль называется вспомогательным алгоритмом, хотя все алгоритмы носят вспомогательный характер. Это название имеет смысл, когда рассматривается динамическое состояние алгоритма; в этом случае можно назвать вспомогательным любой алгоритм, используемый данным в качестве блока (составной части) тела этого динамического алгоритма. Используют и другое название модуля – подалгоритм. В программировании используются синонимы – процедура, подпрограмма.

Свойства модулей:

функциональная целостность и завершенность (каждый модуль реализует одну функцию, но реализует хорошо и полностью);

автономность и независимость от других модулей (независимость работы модуля-преемника от работы модуля-предшественника; при этом их связь осуществляется только на уровне передачи/приема параметров и управления);

эволюционируемость (развиваемость);

открытость для пользователей и разработчиков (для модернизации и использования);

корректность и надежность;

ссылка на тело модуля происходит только по имени модуля, то есть вызов и актуализация модуля возможны только через его заголовок.

Свойства (преимущества) модульного проектирования алгоритмов:

возможность разработки алгоритма большого объема (алгоритмического комплекса) различными исполнителями;

возможность создания и ведения библиотеки наиболее часто используемых алгоритмов (подалгоритмов);

облегчение тестирования алгоритмов и обоснования их правильности ;

упрощение проектирования и модификации алгоритмов ;

уменьшение сложности разработки (проектирования) алгоритмов (или комплексов алгоритмов);

наблюдаемость вычислительного процесса при реализации алгоритмов.

Тестирование алгоритма – это проверка правильности или неправильности работы алгоритма на специально заданных тестах или тестовых примерах – задачах с известными входными данными и результатами (иногда достаточны их приближения). Тестовый набор должен быть минимальным и полным, то есть обеспечивающим проверку каждого отдельного типа наборов входных данных, особенно исключительных случаев.

Пример. Для задачи решения квадратного уравнения ax² + bx + c = 0 такими исключительными случаями, например, будут: 1) a = b = c = 0; 2) a = 0, b, c – отличны от нуля; 3) D = b² – 4ac < 0 и др.

Тестирование алгоритма не может дать полной (100%-ой) гарантии правильности алгоритма для всех возможных наборов входных данных, особенно для достаточно сложных алгоритмов.

Полную гарантию правильности алгоритма может дать описание работы и результатов алгоритма с помощью системы аксиом и правил вывода или верификация алгоритма.

Для несложных алгоритмов грамотный подбор тестов и полное тестирование может дать полную картину работоспособности (неработоспособности).

Трассировка – это метод пошаговой фиксации динамического состояния алгоритма на некотором тесте. Часто осуществляется с помощью трассировочных таблиц, в которых каждая строка соответствует определённому состоянию алгоритма, а столбец – определённому состоянию параметров алгоритма (входных, выходных и промежуточных). Трассировка облегчает отладку и понимание алгоритма.

Процесс поиска и исправления (явных или неявных) ошибок в алгоритме называется отладкой алгоритма.

Некоторые (скрытые, труднообнаруживаемые) ошибки в сложных программных комплексах могут выявиться только в процессе их эксплуатации, на последнем этапе поиска и исправления ошибок – этапе сопровождения. На этом этапе также уточняют и улучшают документацию, обучают персонал использованию алгорима (программы).

В заключение данного раздела приведем общую структуру алгоритмического обеспечения. Критерии, по которым алгоритмы могут быть классифицированы, бывают разными, поэтому предлагаемая ниже схема отражает основные элементы структуры и в некоторых случаях является условной, в том смысле, что блоки приведенной на рис. 9.1 структуры могут "перекрываться".

Рис. 9.1.  Структура алгоритмического обеспечения

Основные формы использования алгоритмов – автономное, библиотечное, пакетное.

Автономный алгоритм определяется решаемой задачей, структурой используемых данных, структурой логических связей частей (модулей) алгоритма и языком {псевдокодов}, на котором представлен, описан алгоритм.

Библиотека алгоритмов определяется множеством задач, решаемых с помощью библиотеки, множеством алгоритмов для решения типовых задач некоторой предметной области и структурой используемых данных.

Пакет алгоритмов, как и библиотека, определяется множеством задач, решаемых с помощью пакета, множеством алгоритмов для решения типовых задач или их составных частей из некоторой предметной области, структурой используемых данных и обменов данными между задачами (модулями), специальным языком, на котором формулируется задание (последовательность этапов решаемой задачи, последовательность задач задания).

10. Лекция: Исполнители алгоритмов - человек и автомат

Рассматриваются основные понятия о базовых исполнителях алгоритмов – человеке и конечном автомате, об их управляющих и исполняющих подсистемах, структурах.

Исполнителем называется некоторая биологическая, техническая или смешанная структура, способная исполнять (покомандно или программно) некоторый класс алгоритмов в некоторой операционной среде (некотором множестве допустимых "инструментов" и "команд").

Наиболее используемые типы исполнителя алгоритмов – человек или автомат (компьютер).

Человек как исполнитель алгоритмов – совокупность исполняющих подсистем (мышечная, двигательная, зрительная, обонятельная и др.) и управляющей подсистемы (нервная, нейронная).

Нервная система передает информацию, получаемую от нервных окончаний кожи, глаз, ушей и других органов, к нервным центрам для ее последующей интеграции, обработки и выработке адекватной реакции. Нервная система – совокупность взаимодействующих нервных клеток или нейронов. У человека их – громадное количество.

Пример. По различным оценкам физиологов, в коре переднего мозга человека – около 50 млрд нейронов. Нейроны, хотя и работают медленно (около сотни инструкций в секунду), но могут за счет более эффективного взаимодействия друг с другом и организации сложнейших нейроструктурных связей (кластеров) решать сложные мыслительные задачи, принимать решения.

Пример. Такая плохо структурируемая, но "простая" для человека задача, как "одеться по погоде", решается быстро с помощью обработки зрительной, слуховой информации и согласованной "нейронной" оценки ситуации, хотя она и плохо формализуемая. Компьютеру эту задачу решать будет намного сложнее. С другой стороны, вычислительные ресурсы человека ограничены по сравнению с возможностями компьютера, который во много раз лучше (быстрее, точнее) решает хорошо формализуемые и хорошо структурируемые задачи.

Нейроны служат для передачи информации за счет нервных импульсов, которая расшифровывается в соответствующих областях коры головного мозга.

В непосредственную (сенсорную) память человека поступает информация от различных сенсоров: зрительных, слуховых, обонятельных и т.д. Затем эта информация переводится в оперативную память (память сознания). Далее она пересылается в долговременную память с привлечением подсознания ("укладывается на полочки" с соответствующими названиями "Формы поведения", "Объекты и образы", "Правила и процедуры обнаружения и идентификации объектов", "Правила выборки и организации информации", "Жизненный опыт", "Бытовые навыки и умения", "Профессиональные навыки и умения" и др.).

Пример. Увиденный человеком конкретный компьютер ассоциируется с абстрактным понятием "Компьютер" (из долговременной памяти) – например со сведениями об этом устройстве – информационными кодами, которые определяют объект (связь, понятие). Коды связываются между собой, создавая образ конкретного компьютера.

В живом организме передача, хранение или обработка информации происходит с помощью биохимических реакций и сообщений – сигнальных молекулярных систем и их превращений за счет химических реакций катализа и разностей концентрации химических веществ. Разность потенциалов действий (электрические сигналы) проводят нервные волокна, с помощью центральной нервной системы. При этом используется и генная информация, которая передается от ДНК к РНК, от РНК – к белку, определяя новую белковую структуру, ее функции.

Второй важный тип исполнителей – конечные автоматы , автоматические (то есть функционирующие определенный промежуток времени без участия человека) устройства, вход, выход и состояния которых можно описать конечными последовательностями сообщений (слов над конечными алфавитами).

Любой конечный автомат реализует некий непустой класс алгоритмов и состоит из совокупности управляющего автомата, который определяет порядок выполнения действий, и операционного автомата, реализующего сами действия, выполняемые автоматом.

Пример. Пример конечного автомата – автомат для продажи газированной воды. Его функционирование можно изобразить графом (рис. 10.1), если ввести следующие множества и события:

X = {1, 3, Г, Ø} – входное множество,

Y = {В, С, О} – выходное множество,

S = {s₀ , s₁ , s₂ , s₃} – множество состояний,

1 – входной сигнал "опустить 1 руб.",

3 – входной сигнал "опустить 3 руб.",

Г – входной сигнал "опустить гнутую монету",

Ø– входной сигнал "монета не опущена",

В – выходной сигнал "выдача воды газированной без сиропа",

С – выходной сигнал "выдача газированной воды с сиропом",

О – выходной сигнал "отказ выдать воду",

s₀ – первое состояние – "начальное состояние",

s₁ – второе состояние – "обработка 1 руб.",

s₂ – третье состояние – "обработка 3 руб.",

s₃ – четвертое состояние – "состояние неисправности".

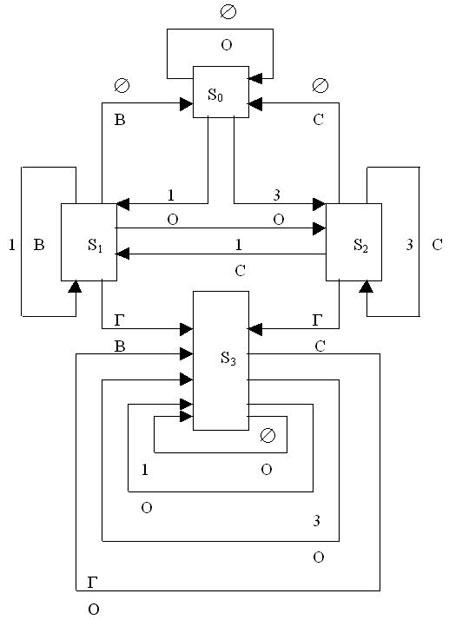Рис. 10.1.  Граф автомата для продажи газированной воды

Функционирование конечного автомата происходит в дискретные моменты времени t = 0, 1, 2, ..., T. Изменение состояния автомата , то есть переход из текущего состояния в новое состояние , может быть осуществлено либо до выдачи выходного сигнала , либо – после выдачи этого сигнала. В связи с этим, выделяют два типа конечных автоматов – автоматы Мили и автоматы Муракоторые различаются законами функционирования автоматов.

Законы функционирования автомата Мили:

Законы функционирования автомата Мура:

Функция выходов f автомата Мура явно не зависит от входного сигнала и полностью определяется только самим внутренним состоянием автомата, которое, в свою очередь, определяется входным сигналом.

Пример. Пример конкретного автомата Мура приведен выше (автомат для газировки). Приведем абстрактный пример автомата Мили: Х = {х₁, х₂} , У = {у₁, у₂, у₃} , S = {s₀, s₁, s₂, s₃, s₄, s₅} , функции перехода и выхода f зададим таблицами соответствий:

– функция перехода
s(t – 1)	S1	s1	s2	s3	s3	s4	s5
x(t)	Х1	х2	x1	x2	x1	x2	х2	x1
s(t)	S2	s3	s4	s2	s4	s3	s5	s5

– функция выхода
s(t – 1)	S1	s1	s2	s2	s3	s3	s4	s5
x(t)	X1	x2	x1	x2	x1	х2	х2	х1
y(t)	У2	у3	y1	y1	y3	у2	у3	y2

Компьютер можно рассматривать как совокупность взаимодействующих конечных автоматов. Рассмотрим такую структуру подробнее.