Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ТА-лекции-2009-10.doc

Скачиваний:

Добавлен:

25.12.2018

Размер:

551.94 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 104 5 6 7 8 9 10 > Следующая >>>

Рекурсивные функции

Еще одним подходом к проблеме формализации понятия алгоритма являются рекурсивные функции. Исторически этот подход возник первым, поэтому в математических исследованиях, посвященных алгоритмам, он имеет наибольшее распространение. Первая формализация понятия алгоритма связана с именами А. Чёрча, К. Гёделя и С. Клини. Идея состоит в том, чтобы выделить класс конструктивно строящихся функций из базовых. Прежде чем рассмотреть базовые (примитивные) функции, приведем некоторые определения.

Рекурсией называется способ задания функции, при котором значение функции при определенном значении аргументов выражается через уже заданные значения функции при других значениях аргументов.

Содержательная идея рекурсивных функций состоит в том, что все исходные данные (аргументы) задачи и ее решения (значения функций) можно пересчитать. То есть рассматриваются функции , заданные на множестве натуральных чисел и принимающие значения в нем же (здесь – n-кратное декартово произведение n на себя, т.е. множество упорядоченных n-ок ). При этом, эти функции могут быть как всюду определенными, так и не всюду определенными, т.е. частичными. Будем считать, что существует единственная нигде не определенная частичная функция.

Частичная функция называется вычислимой, если существует алгоритм, который для входного набора дает на выходе и нуль, если . То есть функция, для которой имеется алгоритм вычисления любого ее значения, называется вычислимой, в противном случае – невычислимой.

Множество M называется перечислимым, если существует алгоритм, позволяющий перечислить все элементы M (возможно, с повторениями).

Например, множество натуральных чисел – перечислимое.

Рассмотрим универсальное множество X и некоторое его подмножество M, т.е. . Подмножество M называется разрешимым в X, если существует алгоритм, который для любого решает проблему: является ли эта точка элементом подмножества M или нет.

Теорема Поста. Подмножество M называется разрешимым в X тогда и только тогда, когда M и дополнение – перечислимые множества.

Рекурсивные функции строятся на основе трех примитивных (заведомо однозначно понимаемых и реализуемых) функций.

Нуль-функция: . Например, 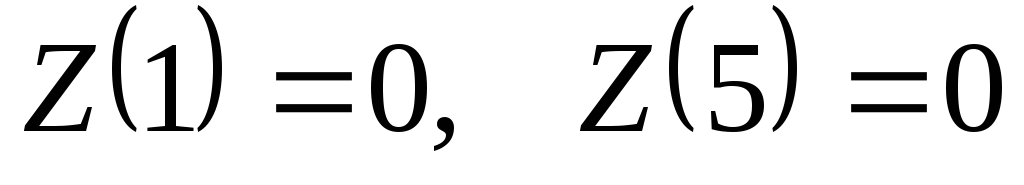, но 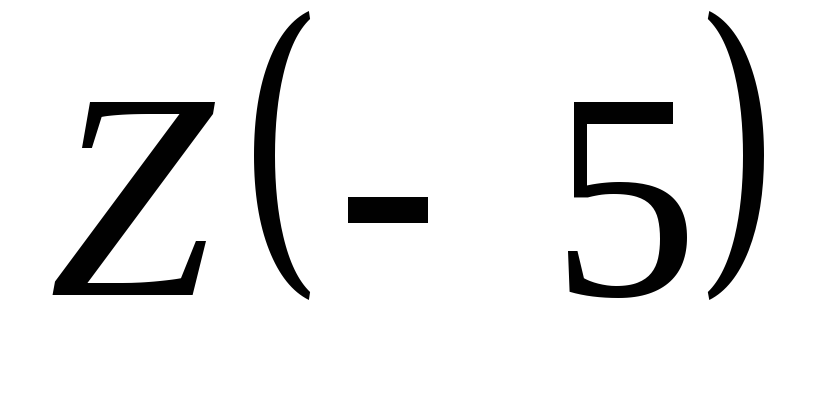– не определено.
Функция следования: Тонкость заключается в том, что операции сложения (+) мы здесь пока не определили и запись " + 1" понимается как взятие следующего элемента естественно упорядоченного множества N. То есть в множестве N всегда можно найти следующий аргумент, например:
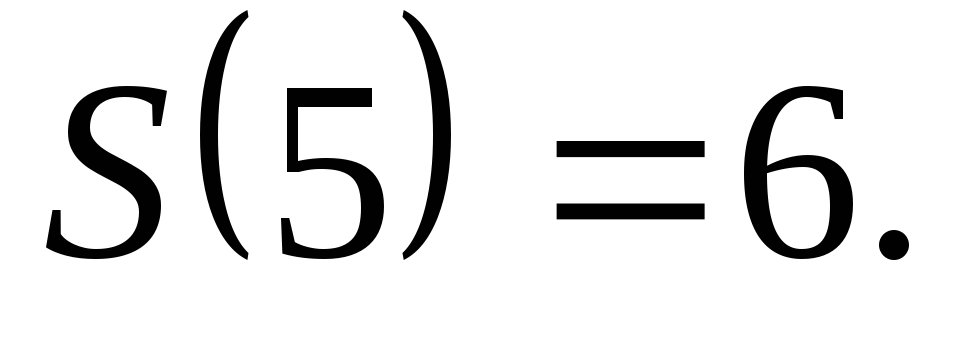
Функция проектирования (выбора аргумента). I_i⁽ⁿ⁾(x₁, x₂,...,x_i,...,x_n) = x_i. Или частный случай – тождественная функция: I(x) = x.

Все эти функции вычислимы в интуитивном смысле.

С примитивными функциями можно производить различные манипуляции, используя три оператора: суперпозиции, примитивной рекурсии и наименьшего корня (-оператор). Они обладают тем свойством, что применяя их к функциям, вычислимым в интуитивном смысле, получаем функции, также вычислимые в интуитивном смысле.

1. Оператор суперпозиции:

Позволяет из функции и функций , , ... , сконструировать функцию .

Например, с помощью оператора суперпозиции можно получить любую константу , где число вложенных функций следования равно n.

Или сдвига числа на константу n, также равную числу вложенных функций следования: .

2. Оператор примитивной рекурсии.

Этот оператор позволяет получить -местную функцию из n-местной и -местной функций. Оператор задается двумя равенствами:

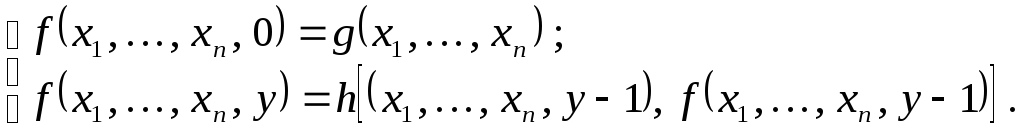
Позволяет по -местной функции получить n-местную. Частный случай – функция одного аргумента:

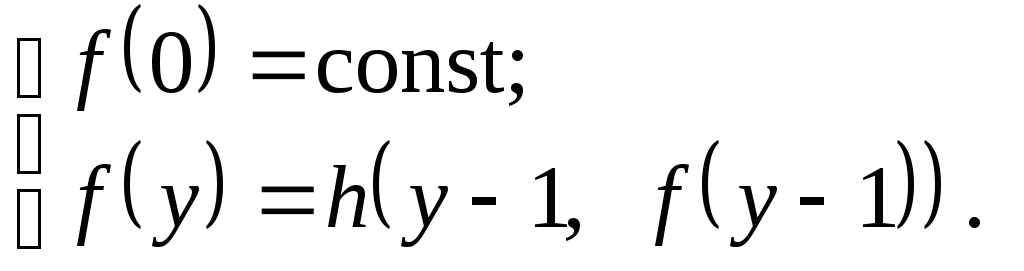
Функции, которые могут быть построены из примитивных с помощью операторов суперпозиции и примитивной рекурсии, называются примитивно-рекурсивными.

Примеры:

а) , т.е. ;

б) функция суммирования . Действительно,

т.е. функция получена из примитивно-рекурсивных функций и

с помощью оператора примитивной рекурсии.

3. Оператор минимизации (-оператор, оператор наименьшего корня).

Говорят, что функция получена из функции с помощью оператора минимизации (или просто -оператора) и обозначают , если определена и равна y тогда и только тогда, когда определены и не равны 0, а . Здесь y – выделенная переменная.

Работу -оператора можно описать следующим образом. Выделяется переменная (здесь – у). Затем фиксируется значение остальных переменных (x₁, ... , x_n). Значение y последовательно увеличивается, начиная с нуля. Значением -оператора будет значение y, при котором функция впервые обратилась в ноль. Значение -оператора считается неопределенным, если функция вообще не принимает значения ноль, либо она принимает отрицательное значение до того, как примет значение ноль.

Пример.

Пусть функция .

Зафиксируем . , т.к. .

Функция называется частично-рекурсивной, если она может быть получена из примитивных функций с помощью операторов суперпозиции, примитивной рекурсии и минимизации.

Множество частично-рекурсивных функций совпадает с множеством вычислимых функций – алгоритмически разрешимых задач. Всюду определенные частично-рекурсивные функции называются общерекурсивными.

Пример.

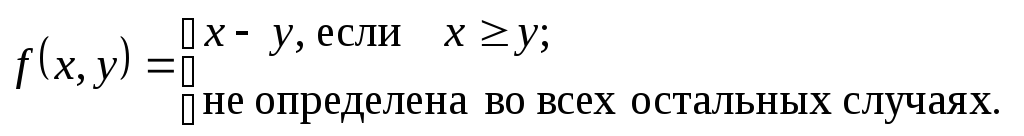
Покажем, что функция частично-рекурсивна. Введем вспомогательные функции (функции усеченной разности):

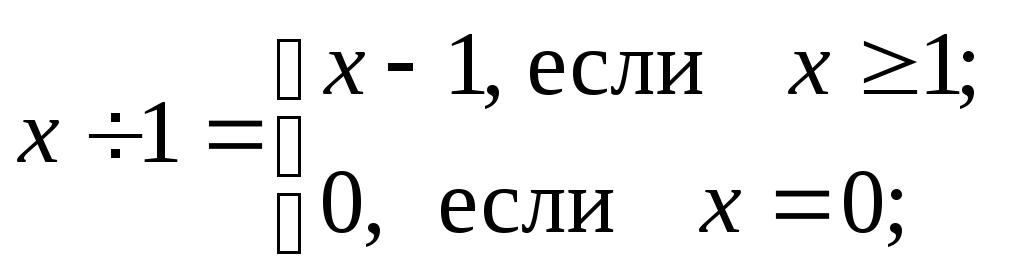
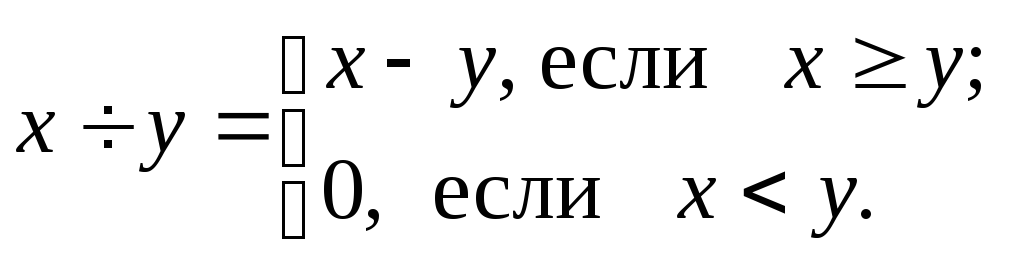
Эти функции примитивно-рекурсивны. Действительно,

Тогда функция также примитивно-рекурсивна. Пусть . Эта функция примитивно-рекурсивна. Функция может быть получена из нее с помощью оператора минимизации: , и, следовательно, она частично рекурсивна.

Из определений очевидно, что каждая примитивно-рекурсивная функция является общерекурсивной, но не наоборот.

-исчисление

-исчисление, основоположником которого считают Алонзо Черча, фактически, и стало основой теории алгоритмов и первой конкретизации алгоритма. -исчисление рассматривают также как основу таких важных разделов математики, как функциональное программирование и комбинаторная логика.

-исчисление (нотация, способ записи) формализует понятие функции не как множества или графика, а как правила.

Выражение в -исчислении представлено в инфиксной форме, например: вместо пишется .

В основе -исчисления лежит операция аппликации.

Аппликация – применение функции к аргументу (можно применить только известную функцию).

Все программы представляются в виде выражений, а процесс выполнения программы заключается в определении значения этого выражения и это называется оценкой выражения.

Оценка выражения производится путем повторения операции выбора и упрощения тех частей выражения, которые можно упростить. Такая часть выражения называется редексом, а операция упрощения – редукцией. Процесс редукции (упрощения) заканчивается, когда выражение не содержит больше редекса, такое выражение называется нормальной формой.

Пример:

Выражение (+(/63)(*25)) сначала редуцируется в выражение (+2 10), а затем приводится к нормальной форме 13.

Язык состоит из:

1. Множества переменных (х₁, ...).

2. Множества констант(с₁, ...).

3. Символа аппликации . .

4. Символа абстракции .

5. Символа равенства =.

-абстракция (-терм) – это одно выражение, определяющее функцию. Например, определяет функцию прибавления к переменной x единицы. Запись показывает, что это выражение является -абстракцией, формальным параметром которой является x. Выражение, которое следует за точкой , является телом -абстракции.

-терм:

1. Переменная или константа – -терм.

2. Если х – переменная, и М – некоторый -терм, то х.М тоже -терм.

3. Если М и N – -термы, то MN тоже -терм.

Формула – любое выражение вида , где M и N – -термы.

Замечание. В литературе прикладного плана нередко используется несколько иная терминология и форма записи.

f = x.x + x

f – название, ранее не названной функции.

 – оператор.

х – аргумент.

. – комбинатор.

х + х – выражение, задающее значение функции.

Пусть имеется выражение , в котором записаны последовательно -абстракция и аргумент 4. При замене x на 4 получим: (+4 1). Это правило преобразования называется -преобразованием.