10.3. Статические критерии диагностики состояний

Все статические критерии трактуют следующим образом: в окрестности всякого диагностируемого состояния N (“норма”) или A (“не норма”) параметры состояния распределены по некоторому статистическому закону, и поэтому мы заранее согласны с тем, что имеется некоторая вероятность ошибки, которую мы будем минимизировать. Получаемые результаты зависят от ряда упрощающих предположений (априорные вероятности состояний , , цена допускаемой ошибки ) и статистических характеристик самого вероятностного распределения (например, в ряде случаев для этого достаточно определить математическое ожидание и дисперсию - для одномерного случая; - либо вектор математических ожиданий и ковариационную матрицу - для многомерных распределений).

Рассмотрим разные случаи (одномерный, 2^х-мерный, многомерный) по мере усложнения.

10.4.1. Одномерный случай – пусть в области изменения параметра X возможны два состояния: (норма – не норма), для каждого из которых известны законы распределения вероятностей .

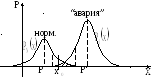
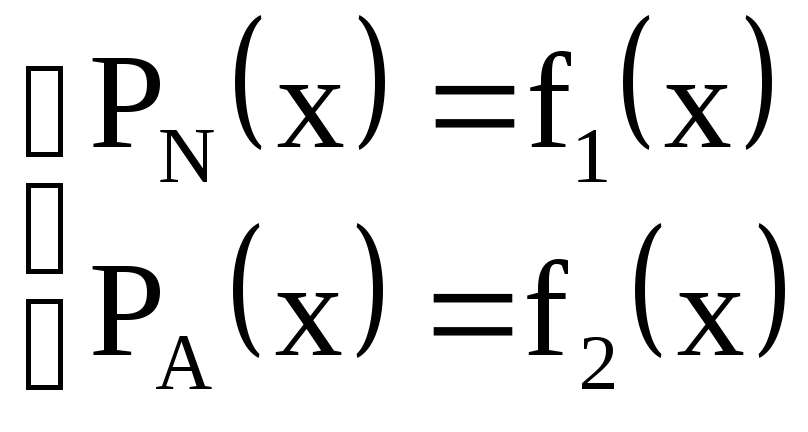
Рисунок 10.3

Как правило, эти вероятности имеют соответствующий максимум в точках и , и существует некоторая область изменения x, в которой с некоторой вероятностью возможны одновременно оба состояния (например, для значения имеем и ). На рисунке эта область заштрихована. Диагностическое правило в этом простом случае стремятся получить в таком виде:

Заметим, что может быть отнесен к состоянию “авария”, но это несущественно.

Если выбор осуществляется по критерию минимального среднего риска (средних потерь от неправильной диагностики), то имеет место следующая система соотношений [ ]:

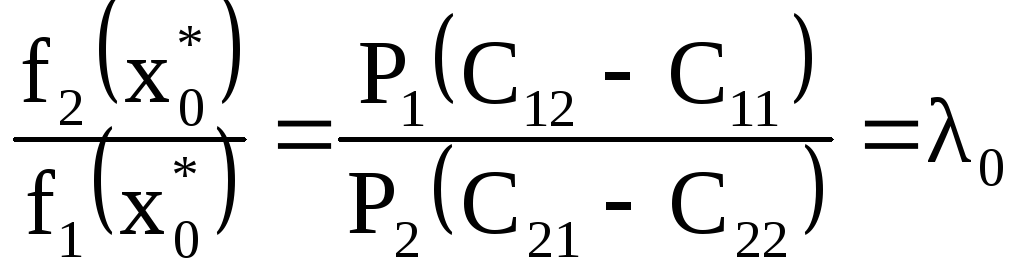
Здесь и - априорные вероятности событий 1-норма и 2-авария, и - потери от ошибочной классификации (объект класса «1» отнесен к классу «2» и наоборот), и - потери (затраты) при правильных решениях.

Отношение принято называть коэффициентом правдоподобия.

Если считать, что параметр x распределен по нормальному вероятностному закону, то

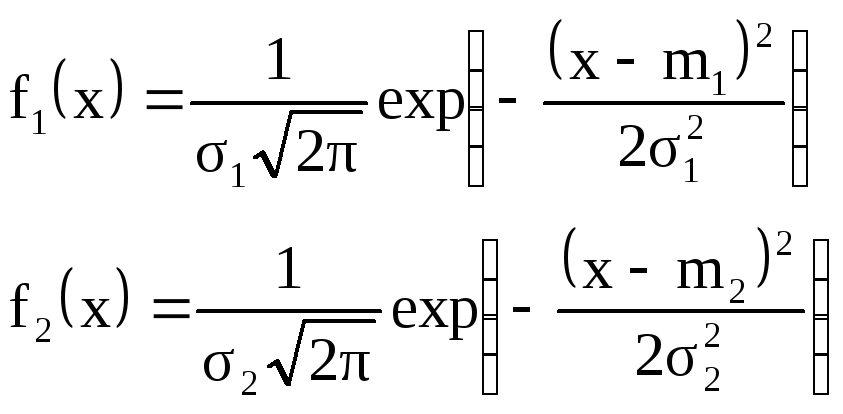
Тогда искомое определяется из соотношения:

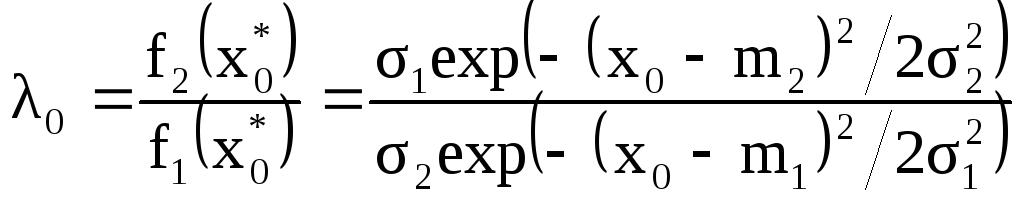
и далее находим, что

Для практического использования имеют значения два наиболее распространенных случая:

а) при одинаковых дисперсиях имеем

б) если матрицы цен и априорные вероятности выбраны так, что , то при одинаковых дисперсиях имеем:

Таким образом, статистическая диагностика в одномерном случае сводится к правилу:

где значение вычисляется по несколько разным формулам, которые удобно привести к общему виду:

,

Здесь значение поправки зависит от ряда дополнительных предположения, что удобно при адаптивных настройках: на ряде шагах процедуры адаптации, в т.ч. при использовании рекуррентного алгоритма обучения:

10.4.2. Рассмотрим теперь диагностику в пространстве двух разных параметров .

Предположим, что в окрестности состояний 1 и 2 определена некоторая область и мы ставим задачу отделить их друг от друга путем построения некоторой вычисляемой функции , такой, что при

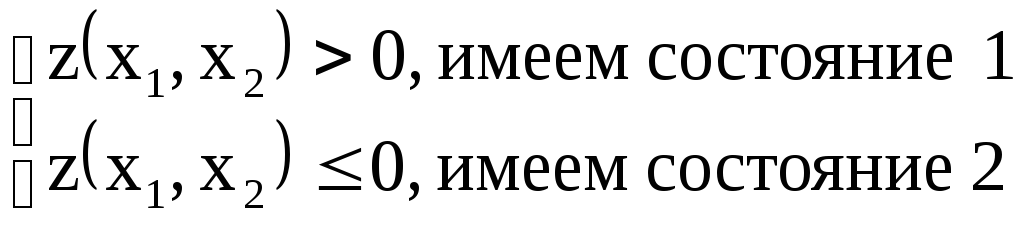
В самом общем случае вид такой функции заранее неизвестен, обычно ее называют дискриминантной функцией

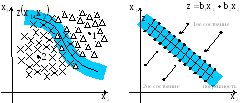
Рисунок 10.4^а Рисунок 10.4^б

Если считать, что при неизвестной нелинейной границе ошибка диагностики минимальна, то согласившись на более простую линейную оценку мы допускаем большую (но допустимую) погрешность (Рисунок 10.4^б). Рассуждая по аналогии с одномерным случаем, разделяющая поверхность представляет собой плоскость, проекция которой на плоскость представляет собой прямую линию вокруг которой выделяют иногда некоторую зону неопределенности, которая определяется различными дополнительными предположениями, в том числе ошибками (особенно если , - вычисляемые показатели, например, характеристики косвенного контроля) измерений.

В зависимости от вида функции различают линейную (ЛДФ) и нелинейную (НЛДФ) дискриминантную функции, к оценке которых мы и перейдем сначала в самом общем виде.

10.4.3. Многомерный случай.

Будем, как и ранее, считать, что для распознавания двух произвольных состояний объекта и в окрестности вектора измерений выполняется многомерный нормальный закон распределения с заданными априорными вероятностями и и основными статистическими характеристиками: вектором математических ожиданий и соответственно ковариационными матрицами , . В ряде работ показано, что по критерию минимальных средних потерь уравнение границы областей удовлетворяет условию (при равных ценах) (НЛДФ) квадратичная форма:

(ЛДФ) при

или иначе для ЛДФ:

Здесь - элементы обратной ковариационной матрицы , а величина порога определяется различными предположениями (априорные вероятности, цены, законы распределения и их параметры).

Как и ранее для одномерного случая, эти уравнения приводятся к рекуррентной форме.

Очень часто мы заранее не знаем типа распределения и тогда достаточно часто используется адаптивный подход: задаемся видом функции и предъявляем обучающей системе точки состояний и , последовательно уточняя коэффициенты . Для случая ЛДФ в многомерном пространстве и при нескольких диагностируемых состояниях алгоритм описанй в [___].

Аналогично работает и процедура классификации на базе кластер-анализа. При этом необходимо задаться мерами расстояний текущих значений точки от центра кластеров и соответственно. Сравнивая каждый раз соответствующие между собой, мы принимаем решение в пользу того состояния, для которого меньше. Заметим, что уравнение границы между состояниями остается неизвестным. Из всех используемых мер расстояний (евклидова мера, взвешенное евклидово расстояние, степенное расстояние (мера Минковского) и др.) наиболее точные результаты классификации получают использованием меры, называемой расстоянием Махаланобиса, которое наилучшим образом приближает равноудаленную точку и сводит процент ошибочных классификаций к минимуму [___]:

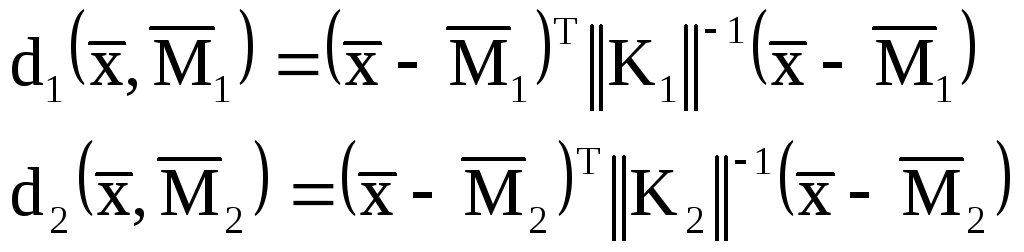
Необходимость на каждом шаге вычислять значительно сложнее, чем определять знак .

Вернемся теперь к двумерному случаю.

В работе [__] показано, что для многомерного нормального закона распределения в пространстве двух параметров и может быть аналитически получена функция формы НЛДФ () от знака которой зависит искомый вид разделяющей кривой для двух состояний 1 и 2:

;

Здесь сделано предположение равенства коэффициента корреляции в обоих состояниях (1, 2).

Вид НЛДФ зависит от знака :

, форма НЛДФ есть эллипс

, форма НЛДФ – парабола

, форма НЛДФ – гипербола.

Заметим, что при изменении R в диапазоне (0,1) парабола имеет место лишь в точке для которой , во всех остальных случаях разделяющая кривая либо эллипс, либо гипербола. Случай линейной границы (ЛДФ) соответствует при этом независимо от изменения R во всем диапазоне (от 0 до 1) возможных значений коэффициентов корреляции при одинаковых дисперсиях.

Примеры определения границ разделяющих поверхностей прямым построением кривых распределения вероятностей приведены ниже на ряде иллюстративных рисунков.

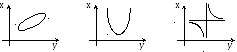
Различные адаптивные процедуры классификации и построения при неизвестных законах распределения и неточных значениях параметров рассмотрены в [____]. В многомерных случаях наилучшие результаты получены при кусочно-линейной аппроксимации исходной НЛДФ.

97