
- •Задание и методические указания к курсовой работе по тау «Расчет регулятора одноконтурной сау
- •Часть 1. Идентификация объекта управления
- •Приближенная (инженерная) аппроксимация.
- •Уточненная аппроксимация.
- •Часть 2. Расчет и оптимизация настроек непрерывного регулятора
- •Часть 3. Анализ процессов в замкнутой сар
- •Задание к курсовой работе
Задание и методические указания к курсовой работе по тау «Расчет регулятора одноконтурной сау
Выполнение курсовой работы состоит из 3 связанных друг с другом частей:
-
идентификация объекта управления по его временным характеристикам;
-
расчет и параметрическая оптимизация настроек непрерывных линейных регуляторов;
-
исследование свойств и анализ процессов в замкнутой САР.
Часть 1. Идентификация объекта управления
Существуют аналитические и экспериментальные методы получения математического описания объектов управления (ОУ). Аналитические методы базируются на использовании уравнений, описывающих протекающие в ОУ физико-химические и энергетические процессы. Однако определить вид дифференциального уравнения динамики недостаточно, поскольку найти коэффициенты уравнения по конструктивным данным ОУ обычно достаточно сложно. Значительно проще провести эксперименты на реальном ОУ и обработать их результаты.
В соответствии с характером воздействия на ОУ экспериментальные методы делятся на частотные методы и методы измерения временных характеристик.
По ряду соображений
предпочтительнее исследовать временные
характеристики. Основным – является
метод исследования реакции объекта на
входное воздействие в виде ступенчатого
сигнала. В этом случае выходной сигнал
представляет собой разгонную
характеристику.
Предварительное определение вида
передаточной функции
![]() ,
соответствующей выбираемой модели ОУ,
может быть сделано по внешнему виду
разгонной характеристики.
,
соответствующей выбираемой модели ОУ,
может быть сделано по внешнему виду
разгонной характеристики.
Физическая
реальность процессов, протекающих в
ОУ, обуславливает необходимость введения
в модель последовательно соединенного
звена идеального транспортного
запаздывания (ИТЗ)
![]() ,
поскольку часто после нанесения
возмущения до начала изменения показателей
процесса проходит некоторое время.
Поэтому выражение для передаточной
функции может быть записано в виде:
,
поскольку часто после нанесения
возмущения до начала изменения показателей
процесса проходит некоторое время.
Поэтому выражение для передаточной
функции может быть записано в виде:
|
|
(1) |
где
значения коэффициентов
![]() определяются характером процессов в
модели ОУ.
определяются характером процессов в
модели ОУ.
Обычно тестируемые ОУ являются устойчивыми (иногда – нейтральными), а переходной процесс носит неколебательный характер. Это означает чисто вещественный характер полюсов и отсутствие нулей у передаточной функции ОУ. Для устойчивого ОУ выражение (1) принимает вид:
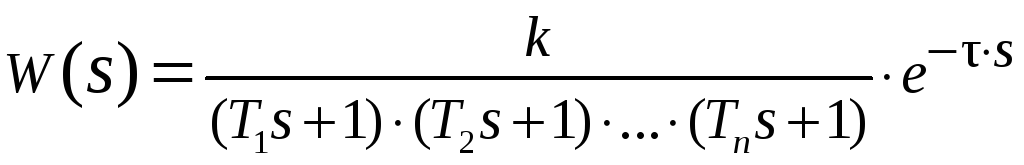 .
(2а)
.
(2а)
Здесь
![]() – коэффициент усиления объекта,
– коэффициент усиления объекта,
![]() –
постоянные времени, соответствующих
наличию распределенных емкостей в ОУ.
–
постоянные времени, соответствующих
наличию распределенных емкостей в ОУ.
В случае нейтрального объекта выражение (1) принимает вид:
 .
(2б)
.
(2б)
Здесь
![]() – время интегрирования нейтрального
ОУ, а остальные обозначения эквивалентны
предыдущей формуле.
– время интегрирования нейтрального
ОУ, а остальные обозначения эквивалентны
предыдущей формуле.
Точно определить число емкостей по накапливанию вещества (или энергии) в ОУ, т. е. создать учитывающую даже мельчайшие особенности поведения модель не представляется возможным. Да это и ни к чему! Часто достаточно провести грубо приближенную или частично уточненную аппроксимацию переходной функции для того, чтобы получить адекватную модель, которую можно использовать для расчета настроек регуляторов.

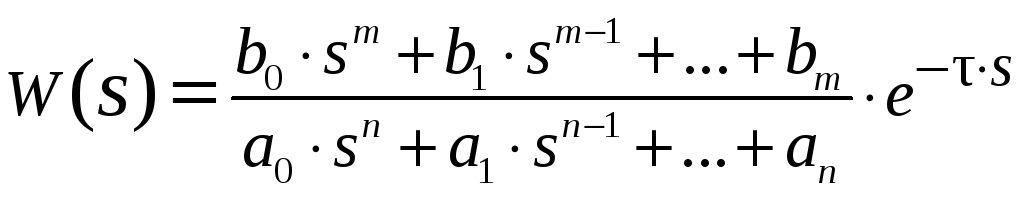 ,
,