26

У зв'язку з мікро- та макронеоднорідністю гум, полуфабрикатів та готових виробів їх, фізичні, механічні та інші характеристики змінюються від одного об'єкту до другого, а також при повторних іспитах. Тому лабораторні та виробничі випробування дають оцінку фактичним властивостям виробів з визначеним ступенем точності (похибки) і надійності (верогідність, достовірність), що залежить від обсягу випробувань, властивостей матеріалу, умов випробувань та інших факторів.

Таким чином похідні рецептури сумішей повинні розроблятися, а властивості гум та готових виробів повинні оцінюватись з використанням математично-статистичних методів та з застосуванням обчислювальної техніки.

Статистична обробка результатів іспитів дозволяє:

• правильно оцінити характеристики вивчаємих властивостей;

• прогнозувати надійність та довговічність виробів в реальних умовах експлуатації;

• науково обгрунтовувати вимоги до похідної сировини та нормативи на готові вироби;

• оцінити вплив технологічних параметрів на стабільність та абсолютний рівень комплексу властивостей полуфабрікатів та кінцевої продукції.

Статистика вивчає масові явища і процеси. Кожному з явищ притаманні як загальні, для усієї сукупності, так і індівідуальні властивості.

СТАТИСТИЧНІ ОЦІНКИ

При оцінці результатів аналізу частіше за все користуються середнім арифметичним, середнє геометричним, а також медіаною та дисперсією. Те чи інше з них обирають відповідно з властивосттями вимирів і в залежності від поставленої задачі.

Середня величина - це статистична оцінка такого розміру ознаки в розрахунку на одну одиницю однорідної сукупності, який однаковий для усіх ознак і сума цих оцінок розмірів ознак сукупності дорівнює сумі спостережуваних розмірів ознак статистичної сукупності.

Для однієї виборки одержані n різних значень х₁; х₂ … х_n , для них середнє арифметичне визначається заформулою:

n

Х = х₁+ х₂ +…+ х_n/ n = 1/ n Σ

i=1

Медіаною (Ме) називають таке значення варіанти, що ділить сукупність за чисельністю на дві рівні частини : із значенням варіант менше та більше медіани.

Для визначення серединного значення Х результат вимірювань записують в порядку, зростання або спадання. Для виборки з n вимірювань це дає ряд х₁< х₂ <…< х_n. Потім визначають серединне значення.

Якщо n - непарне число, тоді варіанта, яка знаходиться в середині послідовності (з індексом k = (n – 1)/2 +1) буде медіаною Ме = Х k.

Якщо n - парне число, то значення медіани розраховується як середнє арифметичне двох варіант, які знаходяться в середині послідовності ранжированих варіант

Ме = (Х _n/2 + Х _n/2+1)/ 2 або Х = (Х₂+Х₃)/ 2

У протилежність середньому арифметичному медіана нечутлива до крайніх результатів вимірювань. Тому вона добре підходить для характеристики невеликих серій вимірювань

( n<10 ).

Крім числових статистичних характеристик важливими є статистичні характеристики варіації.

Окремі результати вимірювань або спостережень більш або менш тісно групуються навколо середнього значення. В якості міри розсіяння використовують стандартне відхилення або розмах.

Стандартне відхилення. Вибіркове стандартне відхилення визначають по формулі:

S = ∑(х_i - Х)²/ (n - 1),

де х_i – окреме значення;

Х – середня усіх Хi;

n - загальна кількість вимірювань;

n-1 – число ступінів волі.

Стандартне відхилення служить мірою відхилення і характеризує випадкову помилку методу аналізу.

Вибірковий розмах – це різниця між найбільшим та найменшим значеннями в упорядкованому ряду:

R=Xmax-Xmin

Вибірковий розмах доцільно використовувати для характеристики розсіяння у вибірках невиликого обсягу для n< 10

Середнє квадратичне відхилення - це абсолютна статистична характеристика варіації, яка характеризує середнє квадратичне відхиленняя ознаки від її середнього значення і має розмірність ознаки

=

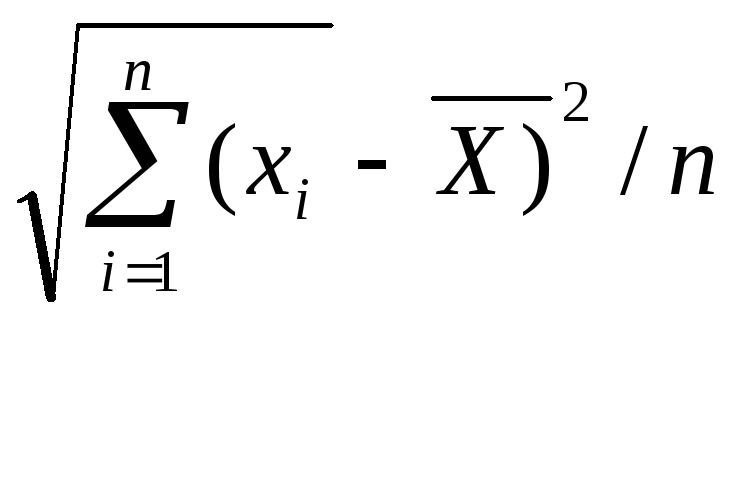
Квадратичний коефіцієнт варіації - це відносна статистична характеристика варіації, яка дорівнює відношенню середньо-квадратичного відхилення ознаки до її середнього значення

Vσ = (σ/ Х)* 100%

За допомогою коефіцієнтів варіації оцінюють однорідність статистичної сукупності. Статистичну сукупність за данною ознакою вважають однорідною, якщо коеффіцієнт варіації менше 33% (Vσ < 33%). За допомогою коефіцієнта варіації здійснюють порівняння варіації однієї ознаки двох статистичних сукупностей.

ВІРОГІДНІСТЬ ПОПАДАННЯ КОНТРОЛЮЄМОГО ПАРАМЕТРУ

У ЗАДАНІ МЕЖІ

У підготовчому виробництві многі причини , або фактори, які не викликають змін у якості гумових сумішей, не є повністю підконтрольними. До таких причин можуть бути віднесені різниця в якості сировини, стан гумозмішуваючого обладнання та кваліфікації робітників, коливання температури, вологості та інш. Все це тягне за собою зміни в якості сумішей або раптові стрибки відхилень деяких показників від середнього значення, через це

зміни якості неможна передбачити. Тому виникає задача прогнозування для даного процесу, що вже встановився , технологічного режиму кількості виготовлення вартих сумішей. У математичному відношенні така задача зводиться до визначення вірогідності попадання випадкової величини у задані інтервали.

Вірогідність попадання ознаки, розподіленною за нормальним законом, на заданий інтервал, визначається за допомогою функції нормального розподілу, що має наступний вигляд:

Величина вірогідності дорівнює площі, що обмежена нормальною кривою та ординатою,яка представляє величину контролюємого параметру.

Вираз для обчислювання вірогідності попадання контролюємого параметру у межі відα до β залежить від обраних нами меж інтегрування. Так верогідність попадання ознаки в інтервал у межах -∞ до λ знаходиться з виразу

Р(α<λ>β )= Ф( ) + Ф ( );

а для випадку коли межі інтегрування становлять відповідно від – λ до λ – з виразу

Р(α<λ>β )= Ф()+Ф(),

де ˉх – середнє значення контролюємого параметру;

σ – середнє квадратичне відхилення.

Користуючись значеннями функції нормального розподілення можна розв’язувати і задачі по визначенню величині вірогідності одержання параметру не більш або не менш якоїсь заданої величини, не більше або не менше середнього значення параметру на обрану величіну ∆= к*σ.

ПОРІВНЯННЯ ВЛАСТИВОСТЕЙ ГУМ ТА ГОТОВИХ ВИРОБІВ

Оцінку якості гум , напівфабрикатів , готових виробів у шинній, гумовій та суміжних галузях виробництва прийнято проводити порівнянням середньоарифметичних величи, що одержані при будь-якому заланому або випадковому числі випробувань. Така практика не враховує статистичного характеру показників , що порівнюються і у деяких випадках може не тільки дати невірну оцінку якості продукції, але й привезвести до аварії. Порівняння цілого ряду показників, у першу чергу тих, які безпосередньо визначають працездатність вироба, повинно проводитися з урахуванням характеру розподілення величин, що обмірюються., з проведенням необхідних статистичних оцінок.

Визначення довірчого інтервалу для середніх значень. Сереня похибка середньогоарифметичного.Якщо середньє арифметичне показника визначається з порівняно невеликої кількості іспитів, то неможна бути впевненим, що одержаний результат точно характеризує середню величину генеральної сукупності. Тому необхідно мати додаткову характеристику, яка дозволила б по часному значенню середнього арифметичного судити про загальну ( генеральну середню арифметичну μ показника, що вивчається).Такою додатковою характеристикою є середня похибка (m), яку обчислюють за формулою

,

де S_x –середнє квадратичне відхилення для вибірки;

n – обсяг вибірки

Середню похибку використовують при оцінці достовірності середнього арифметичного показника. При нормальному розподілі та великій кількості випробувань в 683 випадках з тисячі повинен бути одержан результат, який буде змінюватись у межах:

P=0.683 μ= + m

P=0.954 μ= + 2m

P=0.997 μ= + 3m

У загальному випадку μ= + t m, де t- крітерій Стьюденту. Таблияні значення крітерію Стьюденту наведені у додатку…

Точність визначення середньої похибки. Подібно коефіцієнту варіації, середня похибка може бути виражена у відсотках по відношенню до середнього арифметичного. Ця величина називається показником точності і обчислюється за формулою:

Т= + ,

з якої видно, що чем менш показник точності, тим надійніші результати дослідження. При стандартних механічних випробуваннях гум показник точності складає ± (5÷10)%.

Показник достовірності. В якості показника достовірності викорисовується крітерій Стьюдента t , який представляє відношення різниці між вибірковим середнім арифметичним та генеральною середньою µ до величини середньої помилки m

,

ця формула не може бути використована для обчислювання крітерію але пояснює фізичний вміст крітерію t і використовується для оцінки довірчого інтервалу визначення µ на основі табличних значень t.

У додатку 3 наведені значення t для обсягу вибірки >30. При меншому числі даних величина t визначається в залежності від заданої вірогідності Р та кількості ступенів вільності К (таблиця 9).

У ряді випадків замість поняття вірогідність Р користуються терміном значимість р, при цьому Р=1-р. При розрахунках конструкцій, оцінці якості того або іншого матеріалу, полімерної композиції та інш. необхідно користуваться не середніми значеннями , а значенням мінімуму довірчого інтервалу.

Визначення достовірності розрізнення для двох середніх арифметичних у випадку вибірки великого обсягу.

При великому обсязі вибірки (n>30) достовірність розрізнення між середніми арифметичними визначають за формулою

t=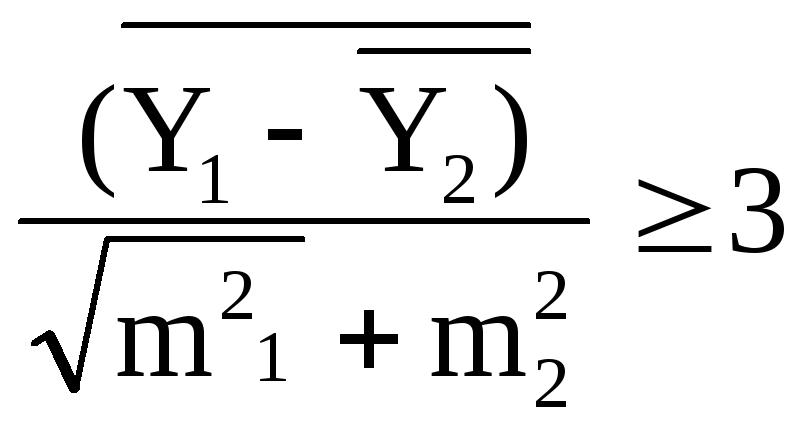

де і - cередні арифметичні показники двох гум;

m₁ ,m₂ - їх середні похибки.

Якщо величина лівої частини більше 3, то різниця між і достовірна. В інших випадках вірогідність розрізнення може бути оцінена по додатку 4.

У першій графі цієї таблиці знаходять цифру, що дорівнюється відношенню ,

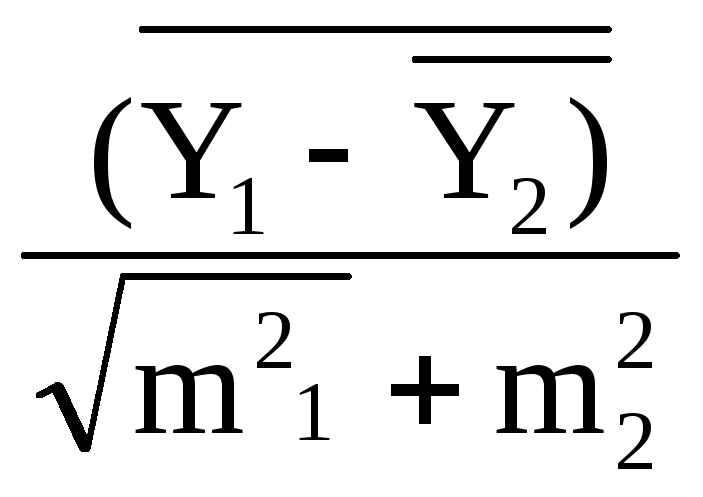а у другій – вірогідність розрізнення у відсотках..

Визначення достовірності розрізнення для двох середніх арифметичних у випадку вибірки малого обсягу ( обсяг менше за 30).

При иалих вибірках достовірність визначають за формулою

t=

де і - cередні арифметичні показники двох гум;

n_1, n₂ - обсяги вибірок для цих гум;

S - середнє квадратичне відхилення, яке визначається за формулою

_{n n}

S=[Σ (Y₁ -)² +Σ (Y_{2 -} )²]/(n₁+n₂ – 2)

У дослідницькій роботі велике практичне значення має питання о кількості необхідних випробувань для одержання середнього арифметичного у гарантованих межах, так як при невеликій кількості випробувань результаті дослідів можуть оказаться ! малонадійними або недостовірними. Мінімально необхідна кількість випробувань залежить від трьох статистических характеристик: коефіцієнту варіації, показника точності та показника достовірності (крітерію Стьюдента).

Визначення мінімальної кількості випробувань. Мінімальну кількість випробувань можна для будь-якого показника визначити за формулою n= V²t²/T², де

V-коефіцієнт варіації, %

t – крітерій Стьюдента при заданій вірогідності Р;

T – показник точності, %.

ОСНОВНІ ПОНЯТТЯ ПРО ДИСПЕРСІЙНИЙ АНАЛІЗ

При виготовленні гумових сумішей існує ряд факторів, які викликають змінність середніх значень показників. Як показує дослід, до таких факторів можуть бути віднесені якість сировини, стан обладнання, рівень кваліфікації працівника, ступінь додержання режиму змішування та інш. Вплив будь-яких із вказаних факторів на мінливість середніх значень показників досліджується за допомогою дисперсійного аналізу.

Основна ідея дисперсіного аналізу складається у порівнянні “факторної дисперсії”, що породжується впливом фактору, та “ залишкової дисперсії”, що обумовлена випадковими причинами. Якщо різниця між цими дисперсіями значима, то фактор оказує суттєвий вплив на досліджуєму сукупність; у цьому випадку середні значень, що спостережуються на кожному рівні ( групові середні) різняться теж значимо.

В залежності від кількості досліджуємих факторів розрізнюють однофакторний, двохфакторний та інш. дисперсійний аналіз.

Дисперсія - це абсолютна статистична характеристика варіації, яка дорівнює середньому квадратів відхилення ознаки від її середнього значення і має розмірність квадрата розмірності ознаки

n

σ² = ∑( х_i - Х)²/ n,

i=1

відповідно для згрупованих статистичних даних обчислюється зважена дисперсія

З наведених формул виходить, що середнє квадратичне відхилення дорівнює квадратному кореню з дисперсії.

При розгляданні статистичної сукупності, яка розбита на групи користуються груповою, міжгруповою та загальною дисперсіями.

Групова дисперсія – це дисперсія значень ознак групи відносно їх середнього значення

^*,

де f _i - частота значень х_j , j- номер групи, - середнє значення j –ої групи,

- обсяг j –ої групи.

Внутрігруповою дисперсією називають середньоарифметичну групових дисперсій, зважену по обсягах груп

де m – число груп.

Міжгрупова дисперсія – це дисперсія групових середніх відносно середньої всієї статистичної сукупності

,

де - середнє значення j-ої групи, - середнє значення всієї статистичної сукупності, -обсяг j-ої групи.

Загальна дисперсія – це дисперсія значень ознаки всієї статистичної сукупності відносно її середнього значення

,

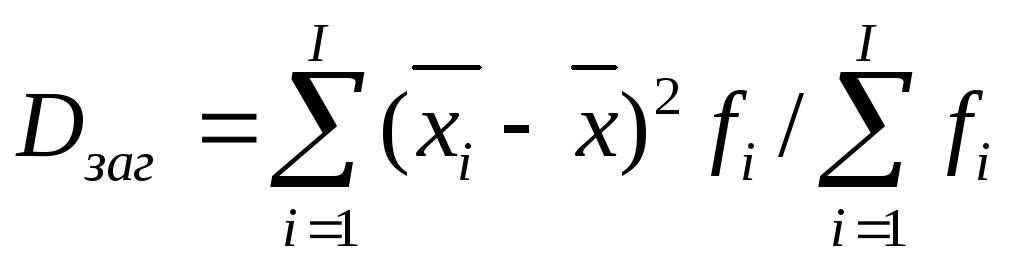де - частоти значень варіант х_i.

Теорема : Якщо статистична сукупність складається з декількох груп, то загальна дисперсія дорівнює сумі внутрігрупової і міжгрупової дисперсій

D _заг = D_внгр + D_міжгр

Техніка дисперсійного аналізу заключається у розкладанні дисперсії вибіркової сукупності на складові, що обумовлені незалежними факторами. За допомогою цих складових проводиться оцінка дисперсії загальної сукупності.

Для визначення значимісті одержаних оцінок їх перевіряють за допомогою таблиць F-крітерію. Якщо вплив розглядаємого фактору має місце, то розраховане значення F-крітерію більш ніж визначене за таблицею. У протилежному випадку вплив розглядаємого фактору не слід брати до уваги.

Коли вплив досліджуємих факторів на мінливість середнього значення має місце, наступним етапом буде оцінка впливу окремих факторів. Для цього використовують t-крітерій, за допомогою якого для випробувань по окремим факторам оцінюють розходження між середніми значеннями.

Розглянемо просту модель однофакторного дисперсійного аналізу, що використовується при перевірці гіпотези о впливі на результати експерименту будь-яких факторів, що належать до одного джерела мінливості.

Нехай на кількістну нормально розподілену ознаку Х впливає фактор F, який має p постійних рівней. Будемо передбачати, що число спостережень на кожному рівні однаково і дорівнюється q.

Нехай спостерігалось n=p*q значень x_ij ознаки X, де i – номер випробування (i=1,2,…,q), j – номер рівня фактору (j=1,2,…,p). Результати спостережень наведені у таблиці.

Таблиця

Номер спостереження	Рівні фактору Fj
	F1	F2	…	Fp
1	x11	x12	…	x1p
2	x21	x22	…	x2p
…	…	…	…	…
q	xq1	xq2	…	xqp
Групова середня			…

Введемо, по визначенню,

(загальна сума квадратів відхилень спостерігаємих значень від загальної середньої ),

(факторна сумма квадратів відхилень групових середніх від загальної середньої, яка характеризує розсіяння “між групами “),

(остаточна сума квадратів відхилень спостерігаємих значень групи від своєї групової середньої, яка характеризує розсіяння “всередені груп”).

Практично залишкову суму знаходять з рівняння :

S_залиш. = S_заг - S_факт.

Нескладними преобразованиями ! одержуємо формули, які більш удобніе ! для розрахунків:

,

,

де Pj= - сума квадратів значень ознаки на рівні Fj; R_j =- сума значень ознаки на рівні Fj.

Примітка. Для спрощення розрахунків з кожного спостерігаємого значення відраховують одней теж стале число С, яке примірно дорівнюється загальній середній. Якщо зменшенні значення у_ij = x_ij-C, то

,

Таким чином , S_факт характеризує вплив фактору F, S_залиш – вплив випадкових причин, а S_заг- відбиває вплив і фактора і випадкових причин.

Коли кількість випробувань на різних рівнях неоднакова, у цьому випадку загальну суму квадратів відхилень знаходять за формулою:

S_заг=[ P₁+P₂+…+P_p]-[(R₁+R₂+…+R_p)²/n],

де P₁=_- -сума квадратів спостерігаємих значень ознаки на рівні F₁ .( інші знаходяться за аналогічним рівнянням)

R₁ = ;R_{2 …} - cуми спостерігаємих значень ознаки на рівнях F₁ , F₂ ,… F_р;

n= q₁ +q₂ +…+q_p загальна кількість випробувань ( обсяг вибірки).

Якщо для спрощення розрахунків з кожного спостерігаємого об’єкту віднімали одней теж стале число С і прийняли, що у_ij=х_ij – C, то

S_заг=[ Q₁+Q₂+…+Q_p]-[(T₁+T₂+…+T_p)²/n].

Факторну суму квадратів відхилень знаходять за формулою:

S_факт = [(R₁ ² /q₁)+ (R₂ ² /q₂)+…+ (R_p ² /q_p)]-[ (R₁+R₂+…+R_p)²/n],

якщо значення ознаки були зменшені (у_ij=х_ij – C), то

S_факт= [(T₁ ² /q₁)+ (T₂ ² /q₂)+…+ (T_p ² /q_p)]-[ (T₁+T₂+…+T_p)²/n].

Інші розрахунки проводять так як і у випадку однакової кількості випробувань:

S_залиш. = S _заг - S_факт,

S ²_факт = S _факт/(p-1), S²_залиш = S_залиш /(n-p).

Модель, в якій один фактор згруповано з іншими, називається двохфакторною моделлю.

Будемо вважати, що задани фактор А з i- рівнями, та фактор В з j-рівнями. Експерименти, що відповідають всім можливим комбінаціям рівней повторюються одне й теж число К>1 раз.

Для двохфакторного дисперсійного аналізусума квадратів відхилень має вигляд :

Q = Q_A +Q_B +Q_R,

а схема аналізу наведена у таблиці.

Середні називають середніми по рядках; а - середніми по стовпцях; - середніми за всіма елементами.

Таблиця

Варіації	Сума квадратів	Число ступенів свободи	Оцінка дисперсії
Між групами А	QA =p	q-1	S
Між групами В	QB = q	p-1	S= QB /(p-1)
Залишкова	QR =	(q-1)*(p-1)	S(q-1)*(p-1)
Загальна	Q =	q*p -1	S2 = Q/(q*p-1)

ВИБІРКОВИЙ МЕТОД. СТАТИСТИЧНА ПЕРЕВІРКА ГІПОТЕЗ.

Вибіркове спостереження – такий вид несуцільного спостереження, при якому обстежуються не всі елементи сукупності, що вивчається, а лише певним чином дібрана її частина. Сукупність, з якої вибирають елементи для обстеження, називається генеральною, а сукупність, яку безпосередньо обстежують, - вибірковою. Обсягом сукупності (вибіркової або генеральної) називають число об’єктів цієї сукупності.Статистичні характеристики вибіркової сукупності розглядаються як оцінки відповідних характеристик генеральної сукупності.

Об’єктивною гарантією того, що вибірка представляє всю сукупність, є додержання наукових принципів організації та проведення спостереження, насамперед неупередженого, об’єктивного підходу до вибору елементів для обстеження.

Принцип випадковості вибору забезпечує всім елементам генеральної сукупності рівні можливості потрапити у вибірку.

Якщо генеральна сукупність містить n елементів, а для обстеження потрібно вибрати з них частину n, то число можливих вибірок

N!

Cⁿ_m = ----------------

n! (N-n)!

Усі вони мають однакову ймовірність 1/Cⁿ_N, але кожна з них несе в собі певну похибку, що відбиває факт випадковості вибору.

Оскільки вибірка статистичної сукупності є випадковою величиною, то і оцінки характеристик є випадковими величинами, які можуть не співпадати із значеннями характеристик статистичної сукупності. Розбіжності між оцінками статистичних характеристик і статистичними характеристиками прийнято називати помилками репрезентативності : для середньої – це різниця між генеральною х₀ та вибірковою х середніми, для частки – різниця між генеральною d₀ і вибірковою p частками, для дисперсії – відношення генеральної ơ₀² та вибіркової ơ² дисперсії.

Вона властива лише вибірковим статистичним спостереженням і залежить від таких факторів: порядку відбору і обсягу вибірки.

За причинами винекнення похибки поділяються на систематичні та випадкові. Систематичні (тенденційні) похибки виникають, коли при формуванні вибіркової сукупності порушений принцип випадковості (упереджений вибір елементів, недосконала основа виборки тощо). Ці похибки для всіх елементів сукупності однонапряплені і призводять до зсунення результатів обстеження.

Випадкові похибки – це наслідок випадковості вибору елементів для дослідження і пов’заних з цим розбіжностей між структурами вибіркової та генеральної сукупностей щодо ознак, які вивчаються.

Згідно з генеральною граничною теоремою за умови достатньо великого обсягу вибірки розподіл вибіркових середніх ( і часток), незалежно від розподілу генеральної сукупності, асимптотично наближається до нормального. Більшість значень вибіркових середніх зосереждується навколо генеральної середньої, а отже, найбільшу ймовірність мають відхилення, близькі до нуля. Чим більше відхилення, тим менша його ймовірність. Для будь-якої ймовірності існує межа відхилень вибіркової середньої від генеральної.

Кінцева мета будь-якого вибіркового спостереження – поширення його характеристик на генеральну сукупність.Для серердньої та частки визначаються межі можливих їх значень у генеральній сукупності з певною ймовірністю – довірчі межі.Якщо метою вибіркового обстеження є визначення обсягових показників генеральної сукупності – обсягів значень ознаки ,то вибіркова середня поширюється на генеральну сукупність прямим перерахунком :

У статистиці використовують два типи оцінок параметрів генеральної сукупності – точкові та інтервальні. Точкова оцінка – це значення параметра за даними вибірки: вибіркова середня та вибіркова частка р. Інтервальною оцінкою називають інтервал значень параметра, розрахований за даними вибірки для певної ймовірності, тобто довірчий інтервал.Чим менший довірчий інтервал, тим точніша вибіркова оцінка.

Межі довірчого інтервалу визначаються на основі точковї оцінки та граничної похибки вибірки Δ=μt:

для середньої х – μt < х₀ >х + μt;

для частки р- μt < d₀ > р+ μt,

де μ – стандартна (середня) похибка вибірки; t – квантиль розподілу ймовірностей (довірче число).

Стандартна похибка вибірки μ є середнім квадратичним відхиленням вибіркових оцінок від значення параметра в генеральній сукупності.

Гранична похибка вибірки Δ=μt - це максимально можлива похибка для взятої ймовірності F(x). Довірче число t показує, як співвідносяться гранична та стандартна похибки.

Рис. Співвідношення ймовірностей та ширини довірчих меж

Як видно з рис., з імовірністю 0,683 гранична похибка не вийде за межі стандартної Δ= + 1μ , з імовірністю 0,954 вона не перевищить + 2μ, з імовірністю 0,997 - + 3μ. На практиці найчастіше застосовують імовірність 0,954 ( на рис. Незашрихована частина площини).

З урахуванням сказаного формули граничних похибок середньої та частки записуються так:

Повторна вибірка Безповторна вибірка

Для се

редньої Δ_x = tσ² ∕n Δ_x = tσ² ∕n(1-n/N) ;

Для частки Δ_р = tpq ∕n Δ_р = tpq ∕n(1-n/N).

Як видно з формул, розмір граничної похибки залежить:

- від варіації ознаки σ²;

- обсягу вибірки n ;

- частки вибірки в генеральній сукупності n/N;

- узятого рівня ймовірнлсті, якому відповідає квантиль t.

За способом організації розрізняють такі види вибіркових спостережень:

• простий випадковий;

• систематичний (механічний);

• типовий;

• серійний.

При простому випадковому спостереженні відбір здійснюють з усієї статистичної сукупності без попереднього розподілу на будь-які групи.

Наступні оцінки результатів контролю

В результаті контролю якості накопичуються дані про кількість дефектних виробів, на базі яких може бути проведен аналіз для оцінки числа або долі дефектної продукції та оцінки рівня якості продукції. Такі оцінки називають наступними, т.я. вони даються після проведення контролю.

За допомогою оцінки числа або долі дефектної продукції можна визначити статистичну підконтрольність або не підконтрольність процесу.

Підконтрольне явище, це явище для якого можна передбачити його майбутнє протікання. Статистично контролюємим називають таке явище, для якого можна спрогнозувати верогідність попадання явища у заздалегідь зазначені межі.

Для перевірки статистичної підконтрольності використовують різні крітерії. Використання того або іншого крітерію залежить від способа упорядкування значень, що спостерігались , від характеру гіпотези, що висувається. Якщо в результаті перевірки підконтрольності процесу процесу будуть обнаружени відхилення від норми, то наступної задачею інженера –технолога стає викриття причин, що визивали ці зміни, а також їх устранениє .

Розглянемо визначення підконтрольності процесу на основі аналізу числа або долі дефектних виробів.

Ідея цього способу заключается у переверці загальної изменчивости для розглядаємого ряду вибірок. Необхідність учета загальної изменчивости у вибірках викликається тими обставинами, що вона може оказатся значительной, не дивлячись на те, що у кожній індивідуальній вибірці контролюємий параетр знаходиться у заданих межах. Для цієї цілі може бути використаний крітерій однорідності . За допомогою цього крітерію за величиною змінності кількості дефектних виробів у різних вибірках дається заключення про те чи є ця величина достатньо великою для того, щоб її можна було пояснити випадковою причиною. Така перевірка носить назву перевірка однорідності.

Величина обчислюється за формулою:

]

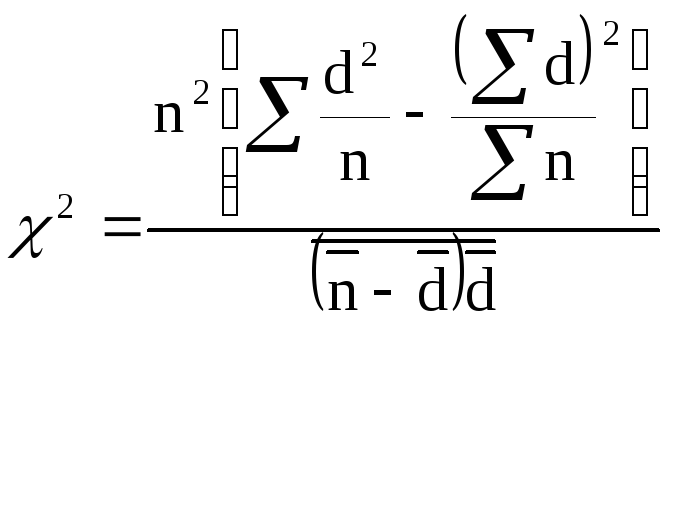де n – кількість виготовлених виробів ( обсяг вибірки);

d – кількість дефектних виробів у виборці;

та означають відповідно та ;

тут К – кількість вибірок, що розглядаються.

Перевірка на однорідність проводиться таким чином. Спочатку за формулою вираховується . Потім розраховується кількість ступенів вільності ν=к-1. З таблиці 5 додатку (с.33 об.) для даних значень та ν знаходиться верогідність одержання значення , що дорівнюється або перебільшує значення , що було одержане по розрахункам. За величиною цієї вірогідності робимо висновок що до випадковості або невипадковості характеру змінності.

Якщо процес перебуває у стані статистичної не підконтрольності наступною задачею стає виявлення причин , що викликали такий стан.

Іншим видом наступних оцінок є оцінки рівня якості продукції. Вони можуть бути використувані для рішення слідуючих питань :

• корегування планів статистичного контролю на основании аналізу результатів контролю;

• одержання порівняльних оцінок якості продукції для різних агрегатів, у різні періоди часу, при зміні технології, для різних заводів , тощо;

• використання оцінок якості як об’єктивних кількостних показників при підведенні підсумків виробничої діяльності, для матеріального стимулювання та ін.

Розглянемо визначення оцінки рівня якості за результатами вибіркового контролю.

Нехай S- кількість партій однакового обсягу N, що були піддані вибірковому контролю; n – обсяг вибірки кожної партії ;m_c- сумарна кількість дефектних виробів в усіх партіях;М- число дефектних виробів у партії.

Доля дефектних виробів у партії дорівнює q=M/N.

Величину оцінки долі дефектних виробів q’ знаходимо з виразу

q’=m_c/S*n

Оцінка кількості дефектних виробів в одній партії М’ відповідно :

М’= q’* N= N*( m_c/S*n).

Загальна оцінка кількості дефектних виробів в усіх партіях :

М’_с = М’* S= m_c*( N/ n).

За цією формулою розраховується оцінка числа дефектних виробів для партій однакового обсягу.

Для партій обсяг яких неоднаков:

а оцінка середнього рівня якості продукції :

Таким чином, оцінка середнього рівня якості продукції для партій являє собою відношення загальної оцінки кількості дефектних виробів до сумарної кількості виробів в усіх партіях.

Оцінка середнього рівня якості продукції при суцільному контролі може бути одержана з останьої формули як часний випадок, коли обсяг вибірки дорівнює обсягу партії

( N=n) і загальна кількість дефектних виробів дорівнює сумі дефектних виробів у кожній партії( m_c=). Тоді середній рівень якості при суцільному контролі можна визначити з відношення загального числа дефектних виробів в усіх партіях до кількості усіх виробів, тобто

ОСНОВНІ МЕТОДИ ОЦІНКИ ЯКОСТІ ЗМІШУВАННЯ

Проблема оцінки якості змішування полімерних систем тісно пов’язані з кількісним описом стану суміші. В залежності від властивостей і відносної кількості окремих інгредієнтів полімерна система може буди віднесена до сумішей з взаємним прониканням компонентів або до сумішей з обокремленими включеннями. В тому або іншому випадку можливе уявлення кожного компоненту у вигляді множини умовних часток однакового предільного обсягу. Це дозволяє застосувати до стану суміші метод статистичного аналізу. При описанні суміші часток кінцевої величини статистичний аналіз базується на використанні поняття випадкової суміші з біномінальним розподілом концентрацій інгрелієнта у пробах малого розміру. Одержання такого розподілення інгредієнтів розглядається як мета технологічного процесу.

Статистичні характеристики розподілення концентрацій окремих або одного інгредієнту в суміші, що одержані при обробці обраної вибірки, порівнюються зі статистичними характеристиками ідеального стану суміші, зокрема -випадкової суміші.Остання характеризується математичним очікуванням концентрації інгредієнта у повному обсязі суміші, тобто похідної концентрації компоненту у загальному складі суміші.генеральна дисперсія біноміального розподілу

σ²=q(1-q)/n, де n – число граничних часток у пробі заданного розміру.

Коефіцієнт варіації біномінального розподілу

k=σ/q =√ (1-q )/nq

Інші ідеалізовані стани суміші, що використовуються для порівняння з досліджуємим, включають також поняття зовсім незмішаної системи, яка характеризується дисперсією концентрації

σ²=q(1-q)

та поняття системи з рівномірним розподіленням інгредієнту по усьому обсягу суміші з дисперсією концентрації σ²=0.

Мірою відхилення стану реальної суміші від випадкової або від інших ідеалізованих станів виражають за допомогою вибіркового середнього та дисперсії вибіркової сукупності проб, взятих з досліджуємої суміші.

До вибіркової сукупності пред’являють вимоги випадковості відбору проб та представительності вибірки, які контролюються відхиленням середньої концентрації Сˉ від загальної концентрації q компоненту у складі суміші. В якості такої міри служить крітерій значимісті даного відхилення :

z= [(C-q)/S]√N

Якщо розраховане значення z більше значення крітерію Стьюденту для рівня значимісті α , то відібрані проби не вдовольняють умовам, що передбачені і їх потрібно замінити іншою вибіркою або прийняти для обробки більшу кількість випробувань. При такій оцінці пред’являють також определенние у відношення кількості ?граничних часток в одній пробі.

В якості міри відхилення реальної суміші від ідеального стану служать слідуючи крітерії:

- індекс змішування I₁= σ²/S²

- крітерій Лейсі I₂= (σ₀² -S²)/( σ₀²- σ²⁾

• інтенсивність розділення I₃ = S²/ σ₀²

• коефіцієнт неоднорідності I₄ = S/q

За допомогою перших двох крітеріїв визначають ступінь приближення до граничного технологічно можливого стану випадкової суміші, що досягається при вельми тривалій переробці. Значення І₁ та І₂ при цьому прагнуть до одиниці. Крітерій Лейсі має область можливих значень 0≤І₂ ≤1, що відповідає переходу від зовсім не змішаної системи до випадкової суміші. Однак, цей крітерій більш зручний для використання до стадії грубого змішування. При тонкому змішуванні оцінка крітерію І₂ втарчає чутливість і він приймає значення близькі до одиниці.

Інтенсивність розділення І₃ та коефіцієнт неоднорідності І₄ представляють собою порівняння з іншим ідеальним станоом суміші – системою з рівномірним розподіленням інгредієнта. Їх граничне значення І ₃= І₄ =0, яке практично не всеж таки не досягається. Значення І₄ обмежено величиною коефіцієнту віріації біноміального розподілу.

Використання статистичних крітеріїв вимагає виконання вимірювань на реальних сумішах, але не дозволяє безпосередньо з їх допомогою прогнозувати результат змішування теоретичним шляхом.

Тепловий баланс каландрів

Рівняння теплового балансу записується у вигляді

Q_N+Q_п=Q_м + Q_вт

де Q_N- кількість тепла, що виділяється за рахунок роботи деформації матеріалу; Q_N =N_срη (N_ср – середня потужність, що споживається та, що витрачається при роботі каландру, кВт; η – коефіцієнт, що враховує втрати питомої теплоємкості на тертя у вузлах приводу); Q_п- кількість теплоти, що подводиться до валка теплоносієм, кВт; Q_м – кількість теплоти , що витрачається на розігрів матеріалу:

Q_м= G _мc_м (t_к – t_п )

G _м- вагова продуктивність каландру, кг/годину; c_м – теплопровідність суміші, що перероблюється, ⁰С;

t_к ; t_п – початкова та кінцева температура суміші, ⁰С;

Q_вт – втрати теплоти до навколишнього середовища:

Q_вт=ΣαF(t_ст-t_ср)

t_{ст ,} t_ср - температура стінки валка та навколишнього середовища,⁰С; F- загальна поверхня тепловіддачі валків:

F = πDLn,

n – кількість валків каландру.

Поверхня, що зайнята стрічкою матеріалу, F₁= Fα /( n*360).

Поверхня, що вільна від стрічки матеріалу, F₂= F - F_1.

Коефіцієнти тепловіддачі розраховуються за формулами:

• для металевої поверхні

α^м_к = 1,18*10^-3√ (t^м_ст – t ^м_ср)/ D;

α^м_л = с₁[(T^м_cт/100)⁴- (T^м_cр/100)⁴] /(t^м_ст – t _ср);

α^м = α^м_к + α^м_л

• для гумової суміші

α^г_к = 1,18*10^-3√ (t^г_ст – t _ср)/ D

α^г_л = с₁[(T^г_cт/100)⁴- (T^г_cр/100)⁴] /(t^г_ст – t ^м_р);

α^г = α^г_к + α^г_л

З умов теплового балансу

Qп = Q_м + Q_вт - Q_N

При відомому значенні Qп визначаємо витрати пари для обігрівання валків:

G= Qп/(i_п- i_к )

де i_п – тепловміст пари при обраному тиску; i_к – тепловміст конденсату.