10.Теорема о структуре общего решения линейного неоднородного дифференциального уравнения второго порядка. Пример.

Теорема:

Пусть - частное решение линейного неоднородного дифференциального уравнения второго порядка , а - общее решение соответствующего линейного однородного дифференциального уравнения второго порядка . Тогда общее решение линейного неоднородного дифференциального уравнения второго порядка имеет следующий вид:

Доказательство:

Пример:

Найти общее решение линейного неоднородного дифференциального уравнения второго порядка:

1)Найдем общее решение соответствующего ему однородного уравнения

2)Найдем частное решение

Приравняем коэффициенты при одинаковых степенях:

3)Построим общее решение :

Ответ: .

11. Метод вариации произвольных постоянных для нахождения частного решения линейного неоднородного дифференциального уравнения второго порядка. Пример.

Метод вариации произвольных постоянных:

Для отыскания частного решения линейного неоднородного дифференциального уравнения второго порядка с переменными коэффициентами

Потребуем, чтобы удовлетворял :

План решения методом вариации произвольных постоянных:

1)Составляем систему для отыскания и

2)По найденным и восстанавливаем и

3)Формируем

Пример:

1)

2)

3)

Ответ: .

12.Решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами. 3 случая. Пример.

Было замечено, что функции вида являются решениями уравнения .

.

. Т.к. , то получим – характеристическое уравнение.

Пример:

Найти общее решение линейного однородного дифференциального уравнения второго порядка:

Ответ:

13.Отыскание частного решения линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами, правая часть которого имеет первый специальный вид.

Первый специальный вид:

- многочлен степени с неопределенными коэффициентами

Степень	Многочлен
0
1
2
3

– число корней характеристического уравнения, совпадающих с .

Пример:

Найти общеее решение линейного неоднородного дифференциального уравнения второго порядка:

1)Найдем общее решение соответствующего ему однородного уравнения

2)Найдем частное решение

Приравняем коэффициенты при одинаковых степенях:

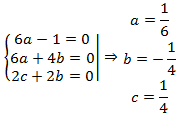
3)Построим общее решение :

Ответ:

14.Отыскание частного решения линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами, правая часть которого имеет второй специальный вид.

Второй специальный вид:

– число корней характеристического уравнения, совпадающих с .

и - многочлены с неопределенными коэффициентами степени

– наивысшая степень многочленов и

Пример:

Найти общеее решение линейного неоднородного дифференциального уравнения второго порядка:

.

1)Найдем корни характеристического уравнения

2)Составим частное решение с помощью второго специального вида правой части:

3)Построим общее решение:

Ответ: