Тема 1. Функции нескольких переменных.

1.Определение функции нескольких переменных. Определение области d. Понятие графика функции двух переменных.

Определение функции нескольких переменных:

Если каждой упорядоченной паре вещественных чисел из некоторой области поставлено в соответствие единственное число , то говорят что на области задана функция двух переменных

Определение области D:

Множество точек из называется областью, если оно удовлетворяет следующим двум условиям:

1)Открытость – Каждая точка множества принадлежит множеству с некоторой своей окрестностью

2)Связанность – Любые две точки множества можно соединить непрерывной кривой, полностью лежащей во множестве .

Понятие графика функции двух переменных:

Совокупность точек пространства называется графиком функции и в общем случае представляет собой поверхность.

2.Определение функции двух переменных, непрерывной в точке. Свойства функции, непрерывной в ограниченной замкнутой области .

Определение функции двух переменных, непрерывной в точке:

Функция называется непрерывной в , если выполняются три условия:

1)Она определена в и некоторой её окрестности.

2)Если существует предел

3)Если

Функция непрерывна в области , если она непрерывна в каждой точке этой области.

Свойства функций, непрерывных в ограниченной замкнутой области :

- является ограниченной в ограниченной замкнутой области

2) достигает в ограниченной замкнутой области своих наибольшего и наименьшего значений.

3) Принимает хотя бы в одной точке этой области любой промежуточное значение между .

3.Определение предела функции двух переменных. Определение частной производной. Пример.

Определение предела функции двух переменных:

Пусть функция определена в некоторой окрестности точки . Число называется пределом функции при и , если для любого существует , такое, что для всех и и удовлетворяющих неравенству выполняется неравенство .

Определение частной производной функции двух переменных:

Частной производной функции по одному из её аргументов называется предел отношения частного приращения функции по этому аргументу к приращению этого аргумента, при условии что приращение .

Пример:

4.Определение функции нескольких переменных, дифференцируемой в точке. Определение полного дифференциала функции. Геометрический смысл частной производной.

Определение функции нескольких переменных, дифференцируемой в точке:

Функция называется дифференцируемой в точке , если её полное приращение в этой точке можно представить в виде , где и при и . Сумма называется главной частью приращения функции.

Определение полного дифференциала функции нескольких переменных:

Главная часть приращения функции , линейная относительно и , называется полным дифференциалом этой функции: .

Для независимых переменных и . Поэтому .

Геометрический смысл частной производной:

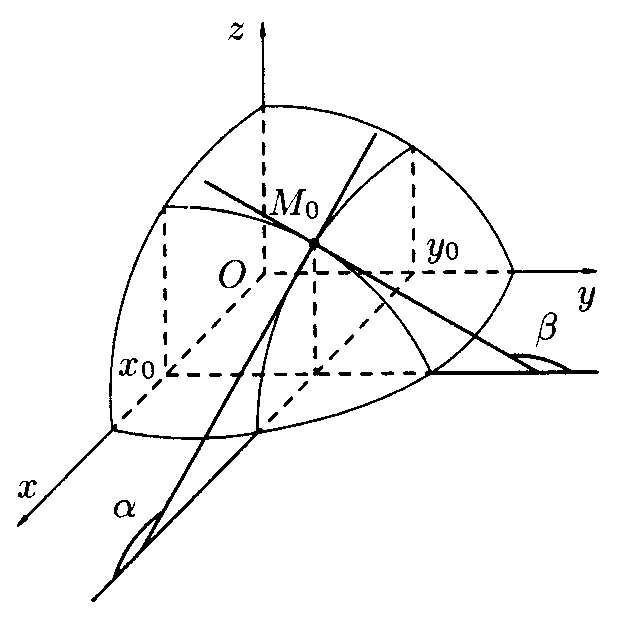Частная производная от функции в точке равна тангенсу гула, составленного осью и касательной к линии , проведенной в .