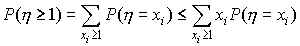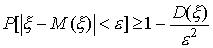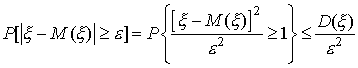Моменты

Математическое ожидание и дисперсия случайной величины X, имеющей гамма-распределение, имеют вид

,

.

Свойства гамма-распределения

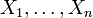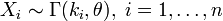• Если — независимые случайные величины, такие что , то

.

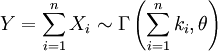• Если 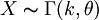, и a > 0 — произвольная константа, то

.

• Гамма-распределение бесконечно делимо.

Связь с другими распределениями

• Экспоненциальное распределение является частным случаем гамма-распределения:

.

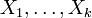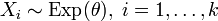• Если — независимые экспоненциальные случайные величины, такие что , то

.

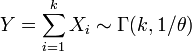• Распределение хи-квадрат является частным случаем гамма-распределения:

.

• Согласно центральной предельной теореме, при больших k гамма-распределение может быть приближено нормальным распределением:

при .

• Если X₁,X₂ — независимые случайные величины, такие ч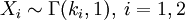то , то

.

Моделирование гамма-величин

Учитывая свойство масштабирования по параметру θ, указанное выше, достаточно смоделировать гамма-величину для θ = 1. Переход к другим значениям параметра осуществляется простым умножением.

Используя тот факт, что распределение Γ(1,1) совпадает с экспоненциальным распределением, получаем, что если U — случайная величина, равномерно распределённая на интервале (0, 1], то − lnU˜Γ(1,1).

Теперь, используя свойство k-суммирования, обобщим этот результат:

где U_i — независимые случайные величины, равномерно распределённые на интервале (0, 1].

Осталось смоделировать гамма-величину для 0 < k < 1 и ещё раз применить свойство k-суммирования. Это является самой сложной частью.

Ниже приведён алгоритм без доказательства. Он является примером выборки с отклонением.

1. Положить m равным 1.

2. Сгенерировать V_{2m − 1} и V_2m — независимые случайные величины, равномерно распределённые на интервале (0, 1].

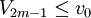3. Если , где 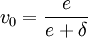, перейти к шагу 4, иначе к шагу 5.

4. Положить 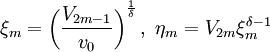. Перейти к шагу 6.

5. Положить .

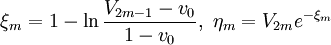6. Если 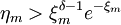, то увеличить m на единицу и вернуться к шагу 2.

7. Принять ξ = ξ_m за реализацию Γ(δ,1).

Подытожим:

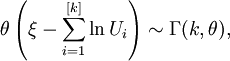
где [k] является целой частью k, а ξ сгенерирована по алгоритму, приведённому выше при δ = {k} (дробная часть k); U_i и V_l распределены как указано выше и попарно независимы.

Вопрос №37

ЗАКОНЫ БОЛЬШИХ ЧИСЕЛ.    1. Леммы Чебышева.

   В этом пункте докажем следующие две леммы, принадлежащие Чебышеву* 1. Леммы Чебышева.

   Лемма 1. Пусть — случайная величина, принимающая только неотрицательные значения; тогда

   Доказательство:    Для простоты докажем это утверждение для дискретной случайной величины , принимающей значения x₁, x₂, ..., x_n, при условии . По аксиоме сложения вероятностей имеем  

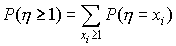
   где суммирование распространено на все значения x_i, большие или равные единице. Но для sub>, очевидно,  

   Поэтому

(50)

   где x_i<1. Эта сумма неотрицательна, так как все по условию, а вероятности . Поэтому

(51)

   Последняя сумма распространена на все значения x_i, принимаемые учайной ветчиной . Но эта сумма по определению равна математическому ожиданию:  

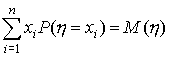
   Сопоставляя соотношения (50) и (51), имеем  

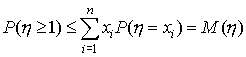
   Лемма 2. Пусть — случайная величина, а - положительное число. Тогда вероятность того, что модуль отклонения случайной величины. от ее математического ожидания окажется меньше, чем , больше или равна разности

(52)

   Неравенство (52) называется неравенством Чебышева.    Доказательство:    Рассмотрим сначала неравенство . Так как оно равносильно неравенству  

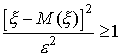
   то

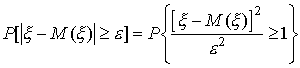
   Случайная величина

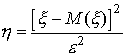
   неотрицательна и, значит, удовлетворяет условиям первой леммы Чебышева. Следовательно,  

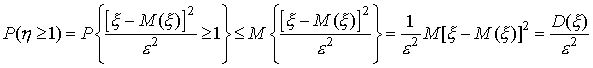
   так как

   Поэтому

   Так как событие, выражаемое неравенством , противоположно событию, выражаемому неравенством , то  

   Принимая во внимание соотношение (53), окончательно получим  

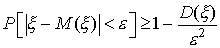
Вопрос №38

Теорема. Каково бы ни было е>0 для любой случай­ной величины X, дисперсия которой конечна, имеет место неравенство Чебышева

Вопрос№39

Вопрос №40

Вопрос№41

Вопрос№42