
- •Список вопросов
- •Расчет магнитных полей соленоида и тороида с использованием теоремы о циркуляции вектора h.
- •Вопрос 1. Электрический заряд. Закон Кулона. Напряженность электростатического поля. Силовые линии. Принцип суперпозиции и его применение к расчету поля бесконечно длинной равномерно заряженной нити.
- •Вопрос 2. Понятие потенциала электростатического поля. Работа поля по перемещению зарядов. Циркуляция вектора е по замкнутому контору.
- •Вопрос 3. Понятие градиента. Связь вектора е и потенциала . Поток вектора напряженности электростатического поля. Дивергенция е.
- •Вопрос 4. Теорема Гаусса в интегральной и дифференциальной форме.
- •Вопрос 5. Теорема Гаусса в дифференциальной форме. Уравнение Пуассона.
- •Вопрос 6. Применение теоремы Гаусса для расчета полей равномерно заряженной плоскости и цилиндра.
- •Вопрос 7. Электрическое поле равномерно заряженное на поверхности сферы. Графики для напряженности и потенциала электростатического поля.
- •Вопрос 8. Расчет вектора напряженности электростатического поля равномерно заряженного по объему шара.
- •Вопрос 9. Проводник в электростатическом поле. Электростатическая индукция. Поле вблизи поверхности заряженного проводника. Результирующее поле и потенциал заряженного проводника.
- •Вопрос 10. Электрический диполь: его характеристики и собственное поле. Поведение диполя в однородном и неоднородном электростатических полях.
- •Вопрос 12. Т-ма Гаусса для диэлектриков. Обобщённая т-ма Гаусса. Вектор электрического смещения. Сторонние и связанные заряды. Связь векторов e, р и d.
- •Вопрос 13
- •Вопрос 14. Электроемкость. Емкость плоского, цилиндрического и сферического конденсаторов.
- •Вопрос 15. Энергия системы неподвижных зарядов. Энергия заряженного проводника и заряженного конденсатора. Энергия электростатического поля. Объемная плотность энергии.
- •Вопрос 16. Носители электрического тока в средах. Дрейф заряженных частиц. Сила и плотность тока. Уравнение непрерывности.
- •Вопрос 17. Электрическое поле в проводнике с током. Силовые линии поля и линии тока. Однородные и неоднородные электрические цепи. Сторонние силы. Эдс цепи.
- •Вопрос 18. Закон Ома в интегральной и дифферинциальной форме. Удельное сопротивление и электропроводность среды.
- •Вопрос 19. Закон Ома для неоднородного участка цепи. Закон Ома для замкнутой цепи.
- •Вопрос 20. Закон Джоуля-Ленца в интегральной и дифференциальной форме.
- •Вопрос 21. Обобщенная сила Лоренца. Движение заряженной частицы в однородных электрическом и магнитном полях. Определение удельного заряда частицы.
- •Вопрос 22. Магнитное поле тока в вакууме. Закон Био-Савара. Принцип суперпозиции для магнитных полей и его применение для расчета поле кругового тока.
- •Принцип суперпозиции
- •Расчет кругового тока.
- •Вопрос 23. Закон Ампера. Магнитный момент контура с током. Контур с током в магнитном поле. Силы и момент сил, действующих на контур, в однородном и неоднородном магнитном поле.
- •Магнитный момент контура с током.
- •Вопрос 24. Работа по перемещению проводника с током в магнитном поле. Понятие магнитного потока. Потокосцепление.
- •Потокосцепление.
- •Работа по перемещению проводника с током в магнитном поле.
- •Вопрос 25. Циркуляция и ротор вектора индукции магнитного поля. Теорема Гаусса для магнитного поля.
- •Вопрос 26. Расчет магнитных полей соленоида и тороида с использованием теоремы о циркуляции вектора h.
- •Вопрос 27. Намагниченность вещества. Циркуляция вектора намагниченности. Магнитная восприимчивость и магнитная проницаемость. Связь векторов магнитного поля: b, j, h.
- •Вопрос 28. Магнитное поле в веществе. Диамагнетики, парамагнетики, ферромагнетики и особенности в их намагниченности.
- •Вопрос 29. Поле на границе раздела двух однородных магнетиков. Условия преломления для векторов b и h.
- •Вопрос 33. Обобщение максвеллом закона электромагнитной индукции. Понятие Вихревого электрического поля. Циркуляция вектора е.
- •Вопрос 34. Циркуляция вектора н с позиции Максвелла. Ток смещения. Закон полного тока.
- •Вопрос 35. Системы уравнений Максвелла в интегральных и дифференциальных формах.
- •Вопрос 38. Излучение электромагнитных волн ускоренно движущимися зарядами и диполем.
- •Вопрос 40. История взглядов на природу света. Волновая и корпускулярная теории света. Шкала электромагнитных излучений.
- •Вопрос 41. Амплитуда и интенсивность электромагнитной волны. Световой вектор. Показатель преломления среды. Длина электромагнитной волны в разных средах.
- •Вопрос 42. Электромагнитная волна на границе раздела двух диэлектрических сред. Коэффициенты отражения и пропускания.
- •Вопрос 43. Принцип суперпозиции электромагнитных волн. Интерференция света. Интерференционное уравнение. Взаимная когерентность световых волн.
- •Вопрос 44. Интерференция от двух когерентных источников. Условия наблюдения на экране интерференционных максимумов и минимумов. Интерференционная зона, ширина интерференционной полосы.
- •Вопрос 45. Временная когерентность электромагнитных волн: время и длина когерентности (на примере опыта Юнга).
- •Вопрос 46. Пространственная когерентность электромагнитных волн (на примере опыта Юнга), ширина когерентности.
- •Вопрос 47. Интерференция в тонких пленках. Полосы равного наклона и равной толщины. Кольца Ньютона.
- •Вопрос 53. Дифракционная решетка как спектральный прибор. Главные максимумы и интерференционные минимумы. Общая дифракционная картина от решетки.
- •Вопрос 54. Спектральные характеристики дифракционной решетки. Угловая дисперсия (определение и расчет). Область дисперсии.
- •Вопрос 55. Спектральные характеристики дифракционной решетки. Разрешающая способность (определение и вывод из критерия Рэлея).
- •24. Разрешающая способность дифракционной решетки.
- •Вопрос 56. Поляризация света. Естественный и поляризованный свет. Виды поляризации. Графический способ представления поляризации.
- •Вопрос 57. Частично поляризованный свет. Степень поляризации.
- •Вопрос 58. Поляризаторы и анализаторы. З-н Малюса.
- •Вопрос 59. Поляризация света при отражении и преломлении. З-н Брюстера.
- •Вопрос 60. Поляризация при двойном лучепреломлении. Обыкновенный и необыкновенный лучи. Распостранение света в одноосных кристаллах. Поляризационная призма и поляроид. Призма Николя.
- •Вопрос 61. Тепловое излучение и его свойство. Основные характеристики теплового излучения. Понятие: абсолютно чёрное тело (ачт), серое тело. Тепловое излучение
- •Спектральная поглощательная способность
- •Вопрос 62. Закон Кирхгофа для теплового излучения. Расчёт испускательной способности реальных излучений.
- •Вопрос 63. Закон Стефана-Больцмана и закон смещения Вина для ачт. Спектр теплового излучения.
- •Спектр теплового излучения
- •Вопрос 64. Гипотеза и универсальная формула Планка для спектральной плотности энергетической светимости ачт. Гипотеза Планка
- •Формула Планка
- •Вопрос 65. Внешний фотоэффект и его законы. Формула Эйнштейна.
- •Вопрос 66. Корпускулярные свойства света. Эффект Комптона. Комптоновская длина волны.
- •Эффект комптона
- •Вопрос 67. Корпускулярно-волновой дуализм материи. Волновые св-ва микрочастиц. Гипотеза де Бройля. Волны де Бройля. Опыты Девиссона – Джермера по дифракции электронов.
- •Вопрос 68. Соотношение неопределённостей Гейзенберга, их применение и следствия.
- •Вопрос 69. Волновая ф-ция, ее назначение и физический смысл. Пл-ть вер-ти обнаружения частицы. Требования (условия) для волновой ф-ции. Принцип суперпозиции состояний
- •Вопрос 70. Стационарные состояния и стационарное ур-ие Шредингера. Собственные значения энергии и собственные ф-ции.
- •Вопрос 71. Микрочастица в одномерной потенциальной яме с бесконечно высокими стенками. Уравнение Шредингера, собственные ф-ции состояния, условие нормировки, квантование энергии частицы.
- •Вопрос 72. Прохождение частицы через высокий потенциальный барьер (туннельный эффект). Коэффициент прохождения (прозрачности) барьера.
- •Вопрос 73. Спектр излучения атома водорода. Ф-ла Бальмера. Постулаты Бора. Элементарная боровская теория водородоподобного атома. Квантование радиусов орбит и энергии электрона.
- •Вопрос 74. Стационарное ур-ие Шредингера для атома водорода. Квантование энергии. Энергия связи электрона. Энергия ионизации.
- •Вопрос 75. Спин, собственные механический и магнитный моменты электрона. Опыты Штерна – Герлаха.
- •Вопрос 76. Квантовые системы из одинаковых микрочастиц. Принцип неразличимости тождественных частиц. Бозоны и фермионы Принцип Паули.
Вопрос 15. Энергия системы неподвижных зарядов. Энергия заряженного проводника и заряженного конденсатора. Энергия электростатического поля. Объемная плотность энергии.
Энергия взаимодействия системы зарядов
![]() Ранее было получено выражение для
потенциальной энергии взаимодействия
двух точечных зарядов qi
и qk:
Ранее было получено выражение для
потенциальной энергии взаимодействия
двух точечных зарядов qi
и qk:
где rik – расстояние между этими зарядами.
![]() Теперь рассмотрим систему из N-точечных
зарядов: q1,
q2,.., qi
,…, qN.
Еще в механике было доказано, что энергия
взаимодействия системы материальных
точек (а сейчас точечных зарядов) равна
сумме энергий взаимодействия каждой
i-ой точки (i-ого
заряда) со всеми оставшимися точками
(зарядами), взятых попарно:
Теперь рассмотрим систему из N-точечных
зарядов: q1,
q2,.., qi
,…, qN.
Еще в механике было доказано, что энергия
взаимодействия системы материальных
точек (а сейчас точечных зарядов) равна
сумме энергий взаимодействия каждой
i-ой точки (i-ого
заряда) со всеми оставшимися точками
(зарядами), взятых попарно:
Если переписать последнее выражение в виде двух последовательных сумм:
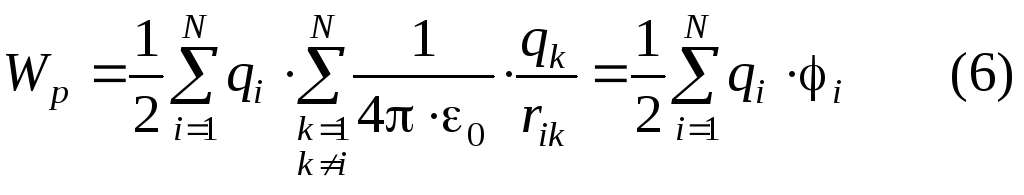
Таким образом, энергия взаимодействия системы зарядов определя-ется как сумма частных произведений (qi∙φi), где φi – потенциал, создаваемый всеми зарядами системы (кроме qi) в точке нахождения заряда qi.
-
Полная энергия взаимодействия системы непрерывно распределенных зарядов
![]() Если заряды распределены непрерывно
(допустим, есть заряженное тело), то,
разлагая заряженную систему на
совокупность элементарных зарядов dq
= ρ∙dV и переходя от
суммирования в (6) к интегрированию по
объему, получаем:
Если заряды распределены непрерывно
(допустим, есть заряженное тело), то,
разлагая заряженную систему на
совокупность элементарных зарядов dq
= ρ∙dV и переходя от
суммирования в (6) к интегрированию по
объему, получаем:
где φ – потенциал, создаваемый всеми зарядами системы в элементе объема dV (в том числе самим зарядом dq).
-
Энергия уединенного заряженного проводника
![]() Пусть проводник имеет заряд q
и потенциал φ. Поверхность проводника
является эквипотенциальной, т.е. везде,
где есть заряд, значение φ – одинаково.
Поэтому для проводника в формуле (7)
потенциал можно вынести из-под знака
интеграла и тогда энергию заряженного
проводника можно определить как
Пусть проводник имеет заряд q
и потенциал φ. Поверхность проводника
является эквипотенциальной, т.е. везде,
где есть заряд, значение φ – одинаково.
Поэтому для проводника в формуле (7)
потенциал можно вынести из-под знака
интеграла и тогда энергию заряженного
проводника можно определить как
![]() а
с учетом определения емкости (3) можно
также записать:
а
с учетом определения емкости (3) можно
также записать:
-
Энергия конденсатора
![]() Пусть +q и φ1
– заряд и потенциал положительно
заряженной обкладки, а −q
и φ2 – заряд и потенциал
отрицательно заряженной обкладки
конденсатора. Тогда, воспользовавшись
формулой (7) и разбив интеграл на две
части (для одной и другой обкладок),
получим энергию заряженного конденсатора
Пусть +q и φ1
– заряд и потенциал положительно
заряженной обкладки, а −q
и φ2 – заряд и потенциал
отрицательно заряженной обкладки
конденсатора. Тогда, воспользовавшись
формулой (7) и разбив интеграл на две
части (для одной и другой обкладок),
получим энергию заряженного конденсатора
а с учетом определения емкости можно также записать:
![]()
Последние две формулы используются в зависимости от условий работы конденсатора: когда на обкладках поддержи-вается постоянным заряд (конденсатор отключен от источника), то
![]()
когда поддерживается постоянным напряжение
![]() (конденсатор
подключен к источнику питания), то
(конденсатор
подключен к источнику питания), то
-
О локализации энергии электрического поля
Формула (7) определяет энергию любой электричес-кой системы через заряды и потенциалы, но эту же энергию можно выразить через основную характеристику поля – напряженность Е. Убедимся в этом на простейшем примере – заряженном плоском конденсаторе.
![]()
![]() Пренебрегая искажением поля у краев
пластин, будем считать поле между
обкладками однородным. Подставив
Пренебрегая искажением поля у краев
пластин, будем считать поле между
обкладками однородным. Подставив
в формулу энергии выражение для емкости плоского конденсатора
получаем:
![]()
Т![]() ак
как для плоского конденсатора U/d
= E и S∙d
= V (объем между
обкладками), то его энергию можно также
представить:
ак
как для плоского конденсатора U/d
= E и S∙d
= V (объем между
обкладками), то его энергию можно также
представить:
Т![]() ак
как электрическое поле в плоском
конденсаторе однородно, то заключенная
в нем энергия распределя-ется с
постоянной (объемной) плотностью
ак
как электрическое поле в плоском
конденсаторе однородно, то заключенная
в нем энергия распределя-ется с
постоянной (объемной) плотностью
![]() В общей теории доказывается, что в
случае изотроп-ного диэлектрика (когда
Е ↑↑ D)
полную энергию поля можно определить
как:
В общей теории доказывается, что в
случае изотроп-ного диэлектрика (когда
Е ↑↑ D)
полную энергию поля можно определить
как:
![]() где
учтено, что D
=ε0∙ε∙E.
При этом объемную плотность энергии
электрического поля можно рассчитывать
по формулам:
где
учтено, что D
=ε0∙ε∙E.
При этом объемную плотность энергии
электрического поля можно рассчитывать
по формулам:
Вывод: Так как эта плотность энергии определяется через напряженность поля, то можно заключить, что энергия локализована в самом электрическом поле.
