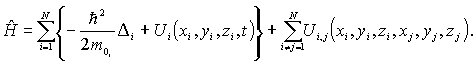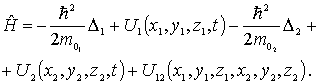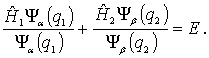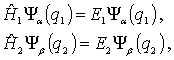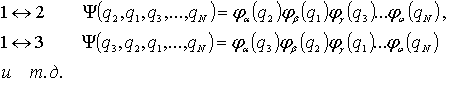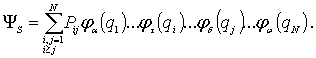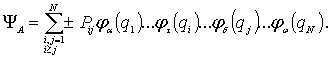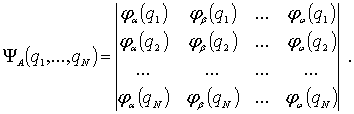1)принцип неразличимости тождественных частиц в квантовой механике. симметричные и антисимметричные состояния тождественных микрочастиц. фермионы и бозоны. принцип Паули. симметричные свойства волновых функций систем тождественных бозонов и фермионов, их связь со спином частиц.

Квантово-механическое описание системы многих частиц

     Важной особенностью микромира является не только то, что микрочастицы обладают существенно иными свойствами по сравнению с макроскопическими телами, но и то, что поведение системы микрочастиц также кардинально отличается от поведения систем, состоящих из макроскопических тел.

     Проведенное до сих пор рассмотрение относилось к случаю квантовых систем, состоящих, как правило, из одной частицы. Некоторые задачи, для которых характерно наличие не одной, а нескольких частиц, например, задача об электроне в атоме водорода или водородоподобном атоме, также были сведены к изучению движения одной частицы - электрона. В данной главе рассматривается квантово-механическое описание систем, состоящих из большого числа микрочастиц.

     Рассмотрим систему, состоящую из частиц с массами . Обозначим координаты - ой частицы через . Под будем понимать координаты центра тяжести частицы ; в качестве обобщенной координаты может выступать и спин частицы , а именно его проекция на выделенное направление. Будем считать, что силы, действующие между частицами, зависят лишь от мгновенных значений их координат и скоростей в данный момент времени, т.е. полагать, что запаздывающее взаимодействие отсутствует. Тогда волновая функция системы частиц может быть представлена в виде

     

     

     Обозначим через . Величина

     

     определяет вероятность того, что одна частица находится в объеме , другая частица находится в объеме и так далее. Таким образом, зная волновую функцию , можно найти вероятность любой конфигурации системы микрочастиц. Кроме того, как и в случае одной частицы, можно определить вероятность какого-либо значения любой механической величины как у системы в целом, так и у отдельной частицы, а также вычислить среднее значение механической величины.

     Волновая функция системы частиц находится из решения уравнения Шредингера

     

     где - оператор Гамильтона для системы частиц. Этот оператор представляет собой обобщение гамильтониана для одной частицы на случай системы многих частиц и имеет вид

     

(6.1)

     Здесь 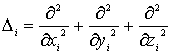, - силовая функция -ой частицы во внешнем поле, а - энергия взаимодействия -ой и -ой частиц.

     В простейшем случае системы, состоящей из двух частиц, оператор есть

     

(6.2)

     Неразличимость тождественных частиц в квантовой механике. Рассмотрим систему, состоящую из одинаковых микрочастиц, т.е. из частиц, обладающих одинаковой массой, электрическим зарядом, спином и т.д. Естественно, что в одинаковых условиях эти частицы будут вести себя совершенно одинаковым образом. Гамильтониан такой системы получается из (6.1), если считать одинаковыми массы всех частиц и силовые функции . Запишем его в виде

     

(6.3)

     Если в системе поменять местами -ю и -ю частицы, то в силу тождественности частиц состояние системы не должно измениться. Неизменной останется полная энергия системы, а также все физические величины, характеризующие ее состояние. Это означает, что гамильтониан системы (6.3) не меняется при перестановке координат и , т.е.

     

(6.4)

     Равенство (6.4) выполняется при перестановке любых двух частиц, образующих систему, и выражает наиболее общее свойство гамильтониана квантовой системы, состоящей из одинаковых частиц: гамильтониан системы одинаковых частиц инвариантен относительно перестановки координат любой пары частиц.

     Введем оператор перестановки частиц в рассматриваемой системе . Действие этого оператора заключается в том, что он переставляет местами -ю и -ю частицы системы. Так, например, если имеется зависящая от координат частиц системы функция , то действие оператора перестановки на эту функцию можно представить следующим образом

     

     Равенство (6.4) с помощью оператора перестановки можно записать в виде

     

(6.5)

     В справедливости (6.5) легко убедиться, подействовав левой и правой частью этого равенства на функцию и получив одинаковый результат. Это означает, что оператор перестановки коммутирует с гамильтонианом системы одинаковых частиц .

     С помощью соотношения (6.5) можно показать, что если волновая функция является решением уравнения Шредингера, то и волновая функция , т.е. функция, получающаяся из перестановкой координат -ой и -ой частиц, также является решением уравнения Шредингера.

     Действительно, пусть волновая функция является решением уравнения Шредингера, тогда

     

     Подействуем на левую и правую части этого уравнения оператором . Так как оператор перестановки не зависит от времени, то его можно внести под знак производной

     

     С учетом соотношения (6.5) получаем

     

     Таким образом, волновая функция также является решением уравнения Шредингера.

     Проводя перестановки любых других пар частиц, мы будем получать все новые возможные состояния системы. Обобщение этого результата можно сформулировать следующим образом: в системе одинаковых частиц реализуются лишь такие состояния, которые не меняются при перестановке частиц местами. Это утверждение получило название принципа тождественности одинаковых частиц. Это очень важный принцип. Он не вытекает из основных постулатов квантовой механики, но и не противоречит им. Его справедливость подтверждается согласием полученных на его основе результатов с опытом.

     Симметричные и антисимметричные состояния. Пусть волновая функция описывает состояние системы, содержащей одинаковых частиц. Действуя на нее оператором перестановки , получаем

     

(6.6)

     Согласно принципу тождественности одинаковых частиц, получившаяся волновая функция должна описывать то же самое состояние, что и исходная волновая функция . Это означает, что эти две функции могут различаться только постоянным множителем. Обозначим его . Тогда уравнение (6.6) можно переписать в виде

     

(6.7)

     Уравнение (6.7) представляет собой уравнение на собственные функции и собственные значения оператора перестановки . Для того, чтобы найти , подействуем на левую и правую части уравнения (6.7) оператором перестановки

     

     Поскольку дважды применяемый оператор перестановки не меняет волновую функцию , то с учетом (6.7) , получаем

     

     т.е. и = . Таким образом, собственными функциями оператора являются функции, которые при перестановке координат -ой и -ой частиц либо остаются неизменными ( ) , либо меняют знак ( ) . Эти функции называются соответственно симметричными и антисимметричными относительно перестановки частиц.

     Полученный результат означает, что состояния системы из одинаковых частиц описываются волновыми функциями, которые либо не меняются (симметричны), либо меняют знак (антисимметричны) при перестановке местами любой пары частиц. В решении задачи 6.1 показано, что волновые функции, описывающие состояние системы, не могут быть симметричными при перестановке одной части частиц системы и антисимметричными при перестановке другой части частиц. Симметрия или антисимметрия волновых функций сохраняется по отношению к перестановкам всех частиц системы.

     Таким образом, принцип тождественности одинаковых частиц в квантовой механике приводит к тому, что все возможные состояния системы, образованной одинаковыми частицами, делятся на два типа:

     симметричные, для которых

     

     и антисимметричные, для которых

     

     Здесь индексы и обозначают, соответственно, симметричную и антисимметричную волновые функции, а перестановки проводятся по всем парам частиц системы. Можно показать (см. решение задачи 6.2 ), что такое деление имеет абсолютный характер, т.е. вид симметрии волновых функций не меняется с течением времени. Если волновая функция, описывающая состояние системы, в какой-либо момент времени является симметричной (антисимметричной), то этот тип симметрии сохраняется и в любой другой момент времени.

     Бозоны и фермионы. Частицы, состояния которых описываются симметричными волновыми функциями, называются бозе-частицами или бозонами. Такое название они получили потому, что системы, состоящие из таких частиц, подчиняются статистике Бозе-Эйнштейна, разработанной индийским физиком Ш. Бозе для фотонов и развитой А. Эйнштейном для идеального газа. К бозонам относятся фотоны, - и - мезоны, фононы в твердом теле, экситоны в полупроводниках и диэлектриках и т.д. Важно отметить, что все бозе-частицы обладают нулевым или целочисленным спином.

     Частицы, состояния которых описываются антисимметричными волновыми функциями, называются ферми-частицами или фермионами. Такое название принято потому, что системы, состоящие из таких частиц, подчиняются статистике Ферми-Дирака, развитой итальянским физиком Э.Ферми и английским физиком П. Дираком. К ферми-частицам относятся электроны, протоны, нейтроны, нейтрино и все элементарные частицы и античастицы с полуцелым спином.

     Эта связь между спином частиц, образующих квантовую систему, и типом статистики была установлена немецким физиком В. Паули. Она остается справедливой и в случае сложных частиц, состоящих из элементарных, таких, например, как атомные ядра, атомы, молекулы и т.д. Ответ на вопрос, является ли сложная частица бозоном или фермионом, зависит от того, каков результирующий спин этой частицы. Если суммарный спин сложной частицы равен целому числу или нулю, то эта частица является бозоном, если же он равен полуцелому числу, то частица является фермионом.

     Рассмотрим в качестве примера ядро атома гелия , т.е -частицу. Оно состоит из двух протонов и двух нейтронов - четырех ферми-частиц, спин каждой из которых равен . Спин ядра равен нулю, т.е. это ядро является бозоном. Атом гелия , содержащий кроме ядра еще и два электрона (две ферми-частицы), также является бозоном. А вот ядро легкого изотопа гелия состоит из двух протонов и одного нейтрона, т.е. нечетного числа (трех) ферми-частиц. Спин этого ядра полуцелый, следовательно ядро является фермионом. Также фермионом является и атом .

     Различие между этими двумя изотопами гелия проявляется не только на микроскопическом, но и на макроскопическом уровне. Оно заключается в том, что жидкий при температуре ~ 2 К обладает сверхтекучими свойствами, а жидкий таких свойств не проявляет. Явление сверхтекучести у было экспериментально открыто отечественным физиком П.Л. Капицей в 1937г и заключается в том, что жидкий может протекать через узкие каналы и щели, не испытывая сил вязкости. Было показано, что сверхтекучесть может возникать только в системе бозонов и связана с образованием так называемого бозе-конденсата - накоплением большого числа бозе-частиц на самом нижнем энергетическом уровне.

     Атомы легкого изотопа гелия являются ферми-частицами, поэтому первоначально казалось, что о сверхтекучести не может быть и речи. Однако впоследствии выяснилось, что при очень низких температурах ~ 0,002 К атомы объединяются в так называемые куперовские пары. Спин такой пары является целочисленным, т.е. куперовская пара представляет собой бозе-частицу. Следовательно, и жидкий в этих условиях может проявлять сверхтекучие свойства. Сверхтекучесть была экспериментально обнаружена в 1974 г.

     Волновая функция системы невзаимодействующих частиц. Найдем с помощью полученных выше результатов вид волновых функций для системы, состоящей из тождественных микрочастиц. В целях упрощения задачи будем считать, что взаимодействие между частицами системы отсутствует, т.е. полагать, что энергии взаимодействия в (6.1) и в (6.2) равны нулю. Сначала проведем решение без учета спина частиц.

     Рассмотрим систему, состоящую из двух одинаковых невзаимодействующих частиц. Согласно (6.2), гамильтониан такой системы есть

     

     где - гамильтониан одной частицы, а - гамильтониан другой частицы, определяемые соотношением

     

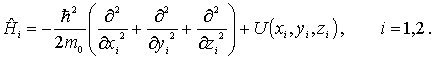
     Отметим, что операторы и совершенно одинаковы, поскольку одинаковы, тождественны сами рассматриваемые частицы. Единственное их различие заключается в том, что операторы и зависят от разных координат.

     Уравнение Шредингера для стационарных состояний системы частиц имеет вид

     

(6.8)

     где - полная энергия системы. Будем решать это уравнение методом разделения переменных

     

(6.9)

     Здесь волновая функция описывает состояние одной частицы, а волновая функция - состояние другой частицы. Подставляя волновую функцию (6.9) в уравнение (6.8), получаем

     

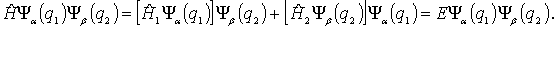
     Разделим левую и правую части этого уравнения на произведение волновых функций

     

(6.10)

     Первое слагаемое в левой части уравнения (6.10) зависит только от координат , второе слагаемое - от координат , тогда как правая часть представляет собой постоянную величину - энергию системы . Это равенство может выполняться только в том случае, если каждое из слагаемых в левой части (6.10) равно постоянной величине

     

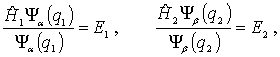
     или

(6.11)

     

     где постоянные величины и удовлетворяют условию .

     Из (6.11) следует, что волновая функция описывает состояние одной частицы с энергией , а волновая функция - состояние другой частицы с энергией . Поскольку частицы не взаимодействуют друг с другом, то полная энергия системы равна сумме энергий отдельных частиц и .

     Обозначим решение первого уравнения в (6.11) через , а второго уравнения в (6.11) - через . Тогда решение уравнения (6.8) для системы двух невзаимодействующих частиц принимает вид

     

(6.12)

     Укажем теперь, как учитывается наличие у частиц спина. Будем считать, что совокупность координат включает в себя не только пространственные компоненты , но и спиновую составляющую - проекцию спина частицы на какое-либо направление. Уравнение Шредингера, которым мы пользовались до сих пор, является уравнением нерелятивистской квантовой механики и не учитывает спин частицы. Поэтому для решения данной задачи необходимо воспользоваться более общим уравнением - уравнением Паули - в котором спин частицы принимается во внимание. Рассмотрение этого уравнения выходит за рамки нашего курса. Отметим только, что решением уравнения Паули является волновая функция, имеющая вид, аналогичный (6.12), т.е. представляющая собой произведение двух волновых функций и , описывающих состояния каждой из частиц. Поэтому в дальнейшем мы будем пользоваться волновой функцией (6.12), считая, что переменные включают в себя как пространственные, так и спиновые координаты.

     Воспользуемся теперь тождественностью частиц. Если в волновой функции (6.12) поменять местами координаты частиц, то получившаяся волновая функция

     

(6.13)

     в силу неразличимости частиц также должна быть решением данной задачи. Однако решения (6.12) и (6.13) не удовлетворяют рассмотренному выше принципу симметрии или антисимметрии волновых функций. Следовательно, состояния, описываемые этими волновыми функциями не могут реализоваться в природе. Но из них можно составить симметричную

     

(6.14)

     и антисимметричную

     

(6.15)

     волновые функции. В силу линейности уравнений квантовой механики эти функции являются решением нашей задачи и могут описывать состояния двух одинаковых бозонов ( ) или двух одинаковых фермионов ( ).

     Обобщим полученные результаты на случай системы, состоящей из тождественных частиц. Используя метод разделения переменных, запишем волновую функцию системы частиц в виде

     

     Перестановка местами каждых двух частиц системы дает новые состояния:

     

(6.16)

     

     В случае системы бозе-частиц, состояния, реализуемые в природе, описываются симметричной комбинацией волновых функций (6.16)

     

(6.17)

     Суммирование в (6.17) проводится по всем возможным перестановкам частиц.

     В случае системы, состоящей из ферми-частиц, получаем антисимметричную комбинацию волновых функций

     

(6.18)

     Здесь знак плюс отвечает четному числу перестановок двух частиц, а знак минус - нечетному. Волновая функция (6.18) может быть представлена в виде определителя

     

(6.19)

     Отметим, что в предыдущих разделах мы использовали, как правило, нормированные волновые функции. В рассматриваемом случае вопрос нормировки не имеет принципиального значения, поэтому функции (6.18) и (6.19) представлены в ненормированном виде.

     Принцип Паули. При отсутствии взаимодействия между частицами системы можно рассматривать не только состояние системы в целом, но и состояние отдельной частицы. Так, например, можно считать, что состояние одной из частиц описывается волновой функцией , другой - и так далее. Такой подход выявляет кардинальное различие между волновыми функциями системы ферми- и бозе частиц.

     Предположим, что в системе ферми-частиц две частицы находятся в одном и том же состоянии, т.е. что . Тогда волновая функция системы обращается в нуль. Действительно, определитель в выражении (6.19) в этом случае имеет два одинаковых столбца, а такой определитель, как известно, равен нулю. Обращение волновой функции в нуль означает, что данное состояние системы физически не реализуемо. Т.е. два фермиона - два электрона, два протона, два нейтрона - не могут находиться в одном и том же состоянии.

     Это положение было сформулировано В. Паули в 1925г и называется принципом или запретом Паули. Принцип Паули гласит: в системе тождественных фермионов не может быть двух частиц, находящихся в одном и том же квантовом состоянии.

     Этот принцип имеет очень важное значение для понимания особенностей поведения ферми-систем, он сыграл большую роль в обосновании периодической системы элементов Д.И. Менделеева, а также для объяснения ряда закономерностей атомных и молекулярных спектров.

     Что же касается системы, состоящей из бозе-частиц, то принцип симметрии волновых функций не накладывает каких-либо ограничений на состояния системы. В одном и том же состоянии может находиться любое число тождественных бозе-частиц.