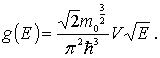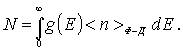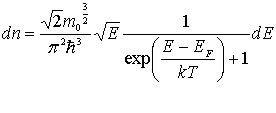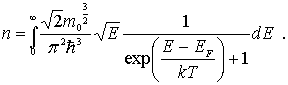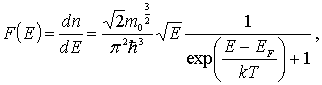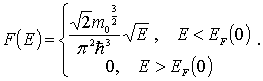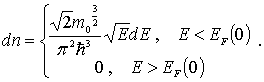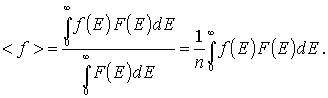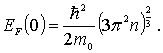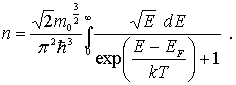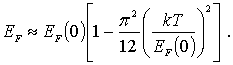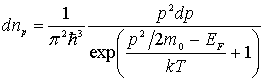Электронный газ в металлах
Применим статистику Ферми-Дирака к описанию поведения электронов проводимости в металлах. Будем пользоваться моделью свободных электронов, согласно которой часть атомных электронов может свободно перемещаться по всему проводнику. Модель свободных электронов в металлах предполагает, что при образовании кристаллической решетки от атомов отщепляются некоторые слабее всего связанные с ними (валентные) электроны. Отщепленные электроны становятся общими для всех атомов и могут свободно перемещаться в кристалле. Именно эти электроны, в отличие от электронов, заполняющих внутренние электронные оболочки атомов, обеспечивают электропроводность металлов. Поэтому их называют электронами проводимости.
Следует отметить, что электроны проводимости в металлах не являются, вообще говоря, абсолютно свободными и испытывают взаимодействие с ионами, находящимися в узлах кристаллической решетки. Однако в первом приближении этим взаимодействием можно пренебречь. Справедливость такого подхода подтверждается, в частности, высокой проводимостью металлов, что может иметь место только в случае достаточно свободного движения электронов внутри проводника. Таким образом, мы будем рассматривать идеальный газ свободных электронов, для которых металлический образец является потенциальной ямой (см. раздел 4.3).
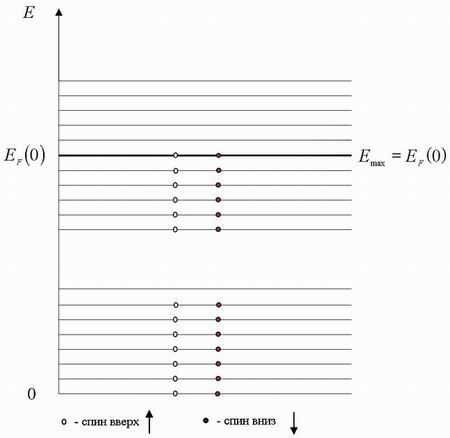
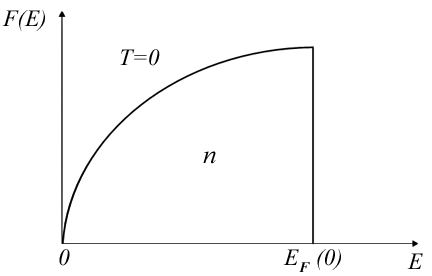
Рассмотрим поведение электронного газа при . В этом случае электроны располагаются на самых нижних доступных для них энергетических уровнях. Согласно запрету Паули в каждом состоянии может находится не более одного электрона, но т.к. электроны могут различаться проекцией спина , то на каждом энергетическом уровне будет находиться по два электрона с различной ориентацией спинов. Схематическое распределение электронов по энергетическим уровням показано на рис.6.10.
Два электрона заполняют самое низшее энергетическое состояние. Третий и четвертый электроны находятся на первом возбужденном энергетическом уровне, следующая пара электронов - на втором
|
Рис. 6.10. |
возбужденном
уровне и т.д. Если число электронов в
металле равно
,
то при
будут
заполнены первые
![]() уровней
с энергией
уровней
с энергией
![]() .
Все остальные уровни с энергией
.
Все остальные уровни с энергией
![]() будут
свободны. Сравнивая полученный результат
с распределением Ферми-Дирака при
,
приходим к выводу, что максимальная
энергия электронов
будут
свободны. Сравнивая полученный результат
с распределением Ферми-Дирака при
,
приходим к выводу, что максимальная
энергия электронов
![]() совпадает
с энергией Ферми
.
совпадает
с энергией Ферми
.
Следует отметить, что хотя энергия электронов в металле квантуется и энергетический спектр электронов является дискретным (см. (6.5)), уровни энергии расположены настолько плотно, что энергетический спектр электронов можно считать практически непрерывным (квазинепрерывным). Численные оценки, подтверждающие справедливость такого подхода, выполнены в задаче 6.5 .
Найдем функцию распределения электронов проводимости по энергии. Плотность квантовых состояний для электронов в металле, т.е. число состояний, приходящихся на единичный энергетический интервал, согласно (6.29) имеет вид
|
(6.51) |
Произведение
на
ширину энергетического интервала
![]() определяет
число состояний, приходящихся на интервал
энергий от
до
определяет
число состояний, приходящихся на интервал
энергий от
до
![]() .
Умножая это произведение на
.
Умножая это произведение на
![]() ,
т.е. на вероятность заполнения данного
энергетического состояния, находим
число электронов
,
т.е. на вероятность заполнения данного
энергетического состояния, находим
число электронов
![]() ,
энергия которых лежит в интервале от
до
,
энергия которых лежит в интервале от
до
![]()
|
(6.52) |
Интегрируя это выражение по энергии, получаем полное число свободных электронов в металле
|
(6.53) |
Выражения
(6.52)
и (6.53)
удобно записывать не для полного числа
электронов в металле
,
а для концентрации электронов
![]() .
С учетом вида
.
С учетом вида
![]() (6.51)
получаем
(6.51)
получаем
|
(6.54) |
и
|
(6.55) |
Функция
|
(6.56) |
входящая
в выражения (6.54)
и (6.55),
называется функцией распределения
свободных электронов по энергиям. При
функция
![]() имеет
вид
имеет
вид
|
(6.57) |
и распределение электронов по энергиям описывается выражением
|
(6.58) |
График
зависимости функции распределения
(6.57)
от энергии при
приведен
на рис. 6.11. Из физического смысла функции
распределения следует, что площадь под
кривой
![]() ,
численно равна концентрации свободных
электронов в металле
.
,
численно равна концентрации свободных
электронов в металле
.
|
Рис. 6.11. |
Отметим,
что функции распределения играют в
статистической физике очень важную
роль. Так, например, если известна функция
распределения частиц по энергиям
,
то можно найти среднее значение любой
физической величины
![]() ,
зависящей от
.
Оно определяется соотношением
,
зависящей от
.
Оно определяется соотношением
|
(6.59) |
Получим
выражение для энергии Ферми
при
.
Для этого воспользуемся соотношением
(6.55)
для концентрации электронов
.
Поскольку при абсолютном нуле температуры
![]() при
и
при
и
![]() при
при
![]() ,
то верхний предел интеграла в (6.55)
нужно заменить на
.
Интегрируя, получаем
,
то верхний предел интеграла в (6.55)
нужно заменить на
.
Интегрируя, получаем
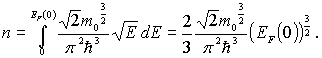
Выражая отсюда , приходим к соотношению
|
(6.60) |
Это
очень важное соотношение, которое
позволяет, зная концентрацию электронов
![]() ,
найти энергию Ферми
,
или, наоборот, по известной энергии
Ферми найти концентрацию свободных
электронов в металле.
,
найти энергию Ферми
,
или, наоборот, по известной энергии
Ферми найти концентрацию свободных
электронов в металле.
Оценим
величину энергии Ферми для свободных
электронов в металле при
.
Пусть
![]() см
-3
=
см
-3
=
![]() м-3
,
тогда
м-3
,
тогда
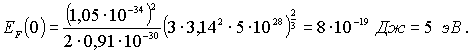
Таким образом, по порядку величины составляет несколько электронвольт.
Наряду
с энергией Ферми вводится понятие
температуры Ферми
![]() ,
которая определяется следующим образом
,
которая определяется следующим образом
|
(6.61) |
Значения
энергии Ферми
,
рассчитанные с помощью соотношения
(6.60)
для различных металлов, приведены в
таблице 6.1. Здесь же даны значения
температуры Ферми
![]() и
скорости Ферми электронов
и
скорости Ферми электронов
![]() ,
найденные с использованием соотношений
(6.61)
и (6.50)
.
,
найденные с использованием соотношений
(6.61)
и (6.50)
.
Рассмотрим
теперь случай ненулевых температур.
Вид распределения Ферми-Дирака при
![]() приведен
на рис. 6.9. Как уже отмечалось, ступенька
в распределении, характерная для
,
в этом случае размывается и переход от
заполненных электронами состояний к
незаполненным происходит более плавным
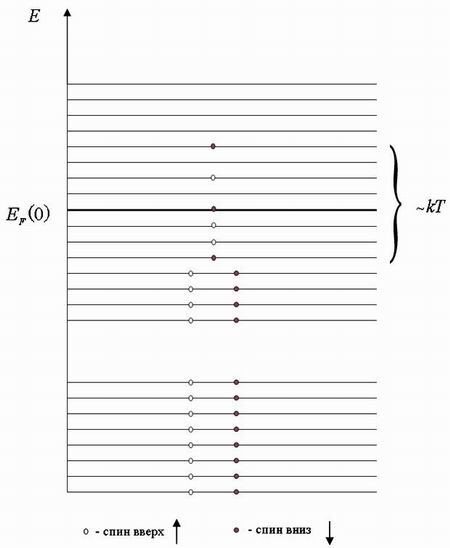
образом. Схематическое распределение
электронов по энергетическим уровням
при
показано
на рис. 6.12.
приведен
на рис. 6.9. Как уже отмечалось, ступенька
в распределении, характерная для
,
в этом случае размывается и переход от
заполненных электронами состояний к
незаполненным происходит более плавным
образом. Схематическое распределение
электронов по энергетическим уровням
при
показано
на рис. 6.12.
|
Рис. 6.12. |
Все состояния, энергия которых меньше энергии Ферми на величину ~ , заняты электронами. Все состояния, энергия которых превосходит энергию Ферми на величину ~ , оказываются свободными. И только в области энергий шириной ~ вблизи энергии Ферми имеются состояния, частично заполненные электронами. Отметим, что хотя ширина этой области, как правило, невелика по сравнению с энергией Ферми, эта область играет очень важную роль. Только электроны, заполняющие состояния в этой области, могут принимать участие в различных физических процессах, происходящих в металлах. Только их энергия может изменяться в ходе этих процессов.
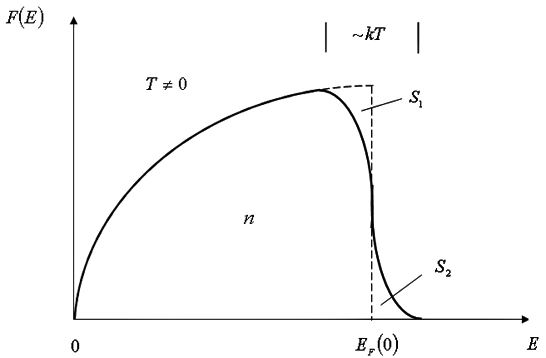
Вид
зависимости функции распределения
от
энергии электронов при
представлен
на рис. 6.13. Поскольку, как и в случае
,
площадь под кривой
численно
равна концентрации свободных электронов
в металле, то площади участков
![]() и
и
![]() оказываются
равными друг другу. Площадь каждого из
этих участков определяет число электронов
в единице объема металла, перешедших
при нагревании образца с заполненных
уровней на незаполненные.
оказываются
равными друг другу. Площадь каждого из
этих участков определяет число электронов
в единице объема металла, перешедших
при нагревании образца с заполненных
уровней на незаполненные.
|
Рис. 6.13. |
Получим выражение для энергии Ферми при отличной от нуля температуре металла. Для этого воспользуемся выражением (6.55), переписав его в виде
|
(6.62) |
Это
выражение позволяет в принципе найти
энергию Ферми
![]() как
функцию температуры
и
концентрации электронов
.
Однако, в общем случае интеграл в (6.62)
точно не берется. Приближенное значение
интеграла удается получить при
как
функцию температуры
и
концентрации электронов
.
Однако, в общем случае интеграл в (6.62)
точно не берется. Приближенное значение
интеграла удается получить при
![]() .
В этом случае для энергии Ферми получаем
.
В этом случае для энергии Ферми получаем
|
(6.63) |
Из
приведенных выше оценок для
следует,
что условие
![]() выполняется
для всего диапазона температур, при
котором металлы существуют в твердом
виде. Это означает, что соотношение
(6.63)
справедливо для всех реализуемых на
практике случаев. Более того, во многих
ситуациях поправка к
,
определяемая выражением (6.63),
оказывается ничтожно малой, так что ей
можно пренебречь и считать, что
выполняется
для всего диапазона температур, при
котором металлы существуют в твердом
виде. Это означает, что соотношение
(6.63)
справедливо для всех реализуемых на
практике случаев. Более того, во многих
ситуациях поправка к
,
определяемая выражением (6.63),
оказывается ничтожно малой, так что ей
можно пренебречь и считать, что
![]() .
Действительно, если взять
.
Действительно, если взять
![]() эВ
, то при комнатной температуре, т.е. при
эВ
, то при комнатной температуре, т.е. при
![]() эВ,
относительная величина поправки к
в
выражении (6.63)
составляет
эВ,
относительная величина поправки к
в
выражении (6.63)
составляет
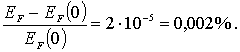
Однако, для понимания ряда физических явлений, таких, например, как поведение теплоемкости металлов при низких температурах или объяснение термоэдс, зависимость от имеет принципиальное значение.
Выше
мы рассмотрели распределение свободных
электронов в металле по энергиям. Наряду
с этим распределением при анализе
поведения электронов в металлах
используются также распределения
электронов по импульсам
и
по скоростям
![]() .
Эти распределения получаются из (6.54),
(6.56)
с учетом того, что
.
Эти распределения получаются из (6.54),
(6.56)
с учетом того, что
![]() ,
а
,
а
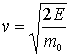 .
Они имеют следующий вид
.
Они имеют следующий вид
|
(6.64) |
и
|
(6.65) |
Эти
распределения, в частности, позволяют
найти средний импульс
![]() и
среднюю скорость
и
среднюю скорость
![]() свободных
электронов в металле.
свободных
электронов в металле.
Вырожденный
электронный газ.
Проведенное в данном разделе рассмотрение
относится к случаю вырожденного
электронного газа, т.е. газа, свойства
которого существенно отличаются от
свойств классического идеального газа
из-за неразличимости одинаковых частиц
в квантовой механике. Отметим, что газ,
состоящий из квантовых частиц, оказывается
вырожденным тогда, когда среднее
расстояние между частицами
![]() становится
меньше или сравнимым с дебройлевской
длиной волны частицы
становится
меньше или сравнимым с дебройлевской
длиной волны частицы
![]() ,
т.е.
,
т.е.
![]() .
Именно с этим связано то обстоятельство,
что квантовые распределения Бозе-Эйнштейна
и Ферми-Дирака в случае разреженных
газов, когда это условие нарушается,
переходят в классическое распределение
Больцмана.
.
Именно с этим связано то обстоятельство,
что квантовые распределения Бозе-Эйнштейна
и Ферми-Дирака в случае разреженных
газов, когда это условие нарушается,
переходят в классическое распределение
Больцмана.
Поведение газа в существенной степени зависит от его температуры. Температурой вырождения называется температура, ниже которой проявляются квантовые свойства газа, обусловленные тождественностью его частиц. Для газа, состоящего из бозе-частиц, температура вырождения определяется как температура, ниже которой происходит бозе-конденсация, т.е. переход заметной доли частиц в состояние с нулевой энергией. Именно с бозе-конденсацией связаны такие интересные физические явления, как сверхтекучесть жидкого гелия, т.е. его способность протекать через тонкие щели и капилляры без какой-либо вязкости, и сверхпроводимость некоторых металлов и сплавов.
Для
газа, состоящего из ферми-частиц,
температурой вырождения является
температура Ферми
,
определяемая соотношением (6.44)
. Как следует из (6.44),
температура вырождения тем больше, чем
меньше масса частиц и чем больше их
концентрация, поэтому
![]() особенно
велика у электронного газа в металлах.
Действительно, масса электрона очень
мала (
особенно
велика у электронного газа в металлах.
Действительно, масса электрона очень
мала (![]() кг),
а концентрация электронов в металлах
достаточно велика (
~
кг),
а концентрация электронов в металлах
достаточно велика (
~![]() м-3),
что приводит к значению
~
м-3),
что приводит к значению
~![]() К
(см. Таблицу 6.1). При температуре
К
(см. Таблицу 6.1). При температуре
![]() ,
т.е. при
,
т.е. при
![]() ,
электронный газ в металлах является
вырожденным. При температуре
,
электронный газ в металлах является
вырожденным. При температуре
![]() ,
т.е. при
,
т.е. при
![]() ,
электронный газ невырожден. Поскольку
температура Ферми для металлов имеет
величину
~
,
электронный газ невырожден. Поскольку
температура Ферми для металлов имеет
величину
~
![]() K,
то электронный газ в металлах оказывается
вырожденным при всех температурах, при
которых металл остается в твердом
состоянии.
K,
то электронный газ в металлах оказывается
вырожденным при всех температурах, при
которых металл остается в твердом
состоянии.
В полупроводниках характер поведения электронного газа зависит от величины концентрации носителей заряда. В примесных полупроводниках при высокой концентрации донорной примеси электронный газ может оказаться вырожденным. В полупроводниках с акцепторной примесью свойствами вырожденного газа может обладать газ дырок. Такие полупроводники называются вырожденными полупроводниками.
Для обычных газов, состоящих из атомов или молекул, являющихся ферми-частицами, температура вырождения близка к абсолютному нулю. Поэтому такие газы во всей области температур вплоть до температуры сжижения являются невырожденными и подчиняются классической статистике Максвелла-Больцмана.