
- •Лекция 1. Метод математической индукции.
- •Принцип индукции.
- •Неравенство Коши-Буняковского.
- •Лекция 2. Комбинаторика.
- •Принцип умножения.
- •Перестановки.
- •Размещения.
- •Рассмотрим первый набор чисел.
- •Сочетания.
- •Некоторые свойства биномиальных коэффициентов:
- •Перестановки с повторениями.
- •Сочетания с повторениями.
- •Бином Ньютона.
- •1). База индукции.
- •2). Индуктивное предположение.
- •3). Индуктивный переход.
- •Лекция 3. Введение в теорию множеств. Понятия о множестве.
- •Два основных интуитивных принципа наивной теории множеств.
- •Интуитивный принцип объемности.
- •Интуитивный принцип абстракции.
- •Парадокс Рассела.
- •Лекция 4. Операции над множествами. Сравнение множеств.
- •Свойства отношения включения.
- •Операции над множествами.
- •Лекция 5. Свойства операций над множествами.
- •Формула включения и исключения.
- •Лекция 6.
- •Упорядоченные пары.
- •Прямое произведение множеств.
- •Бинарные отношения.
- •Композиция отношений.
- •Теорема о свойствах бинарного отношения.
- •Матрицы конечных бинарных отношений.
- •Свойства матриц конечных бинарных отношений.
- •Матрицы объединения и пересечения двух бинарных отношений.
- •Матрица композиции двух конечных бинарных отношений.
- •Матрица обратного отношения.
- •Матрица рефлексивного бинарного отношения
- •Ядро бинарного отношения.
- •Свойства ядра:
- •Лекция 8. Отношения эквивалентности.
- •Классы эквивалентности.
- •Функции.
- •Инъекции и биекции.
- •Примеры экзаменационных задач.
- •Лекция 9. Композиция функций.
- •Ядро функции).
- •Отношения порядка.
- •Экстремальные элементы в упорядоченном множестве.
- •Лекция 10. Верхняя и нижняя грани частично упорядоченного множества.
- •Решетки.
- •Ограниченные решетки.
- •Решетки с дополнением.
- •Частичный порядок в решетке.
- •Лекция 11. Матроиды.
- •Максимально независимые подмножества.
- •Алгоритм построения базы матроида.
- •Ранг множества.
- •Жадный алгоритм.
Бинарные отношения.
Пусть А и В – два произвольных множества.
Определение 3. Бинарным
отношением
![]() из множества А в
множество В называется
всякое подмножество прямого произведения
А на В; если А=В, то говорят
о бинарном отношении на множестве
А. Обозначение:
из множества А в
множество В называется
всякое подмножество прямого произведения
А на В; если А=В, то говорят
о бинарном отношении на множестве
А. Обозначение:
![]()
Пример 2.
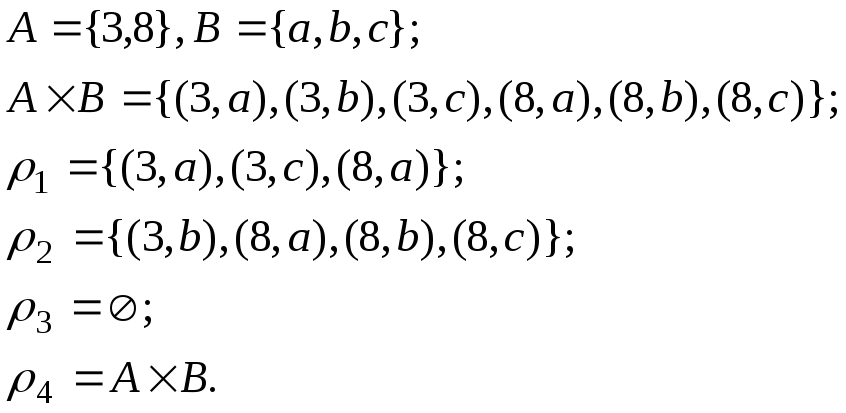
Используют две формы записи принадлежности некоторой упорядоченной пары заданному бинарному отношению:
Инфиксная:
![]()
Префиксная:
![]()
По аналогии с бинарным отношением вводят понятие n – арного отношения произвольного подмножества упорядоченных n – ок, выбранных из прямого произведения данных n множеств.
Пример 3.
M – множество;
2M – булеан множества M;
бинарное отношение включения на
![]() определяется так:
определяется так:
![]()
Определение 4. Множество
точек плоскости, координаты которых
(x,y),
образуют упорядоченные пары некоторого
бинарного отношения
![]() называется графиком данного
бинарного отношения.
называется графиком данного
бинарного отношения.
Пример 4.
1).
![]()
2 0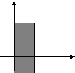
График
![]()
2).
![]()

График
![]()
Бинарные отношения – это множества, их можно объединять, пересекать, дополнять и т. д.
Пример 5.
1).
![]()
2 0 1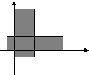
График
![]()
2).
![]()
0 1 2
График
![]()
Пусть
![]()
Определение 5. Областью
определения бинарного отношения
(обозначение:![]() ),
называется подмножество множества А
такое, что
),
называется подмножество множества А
такое, что
![]()
Пусть
![]()
Определение 6. Областью
значения бинарного отношения
(обозначение:
![]() ),
называется подмножество множества В
такое, что
),
называется подмножество множества В
такое, что
![]()
Пусть
![]()
Определение 7. Отношением,
обратным к отношению
![]() ,
называют подмножество прямого произведения
,
называют подмножество прямого произведения
![]() ,
такое, что
,
такое, что
![]() .
.
Пример 6.
![]()
![]()
Определение 8. Дополнением
отношения
![]() называют бинарное отношение, определяемое
как множество всех упорядоченных пар,
не входящих в
называют бинарное отношение, определяемое
как множество всех упорядоченных пар,
не входящих в
![]() :
:
![]()
Пример 7.
![]()
![]()
Определение 9. Тождественным
отношением I
называют подмножество А2
такое, что
![]()
Пример 8.
![]()
Определение 10. Универсальным
отношением U
называют само прямое произведение
множеств
![]()
Композиция отношений.
Пусть
![]()
Определение 11. Композицией
отношений
![]() называют бинарное отношение из множества
А во множество В, определяемое
так:
называют бинарное отношение из множества
А во множество В, определяемое
так:
![]()
Пример 9.
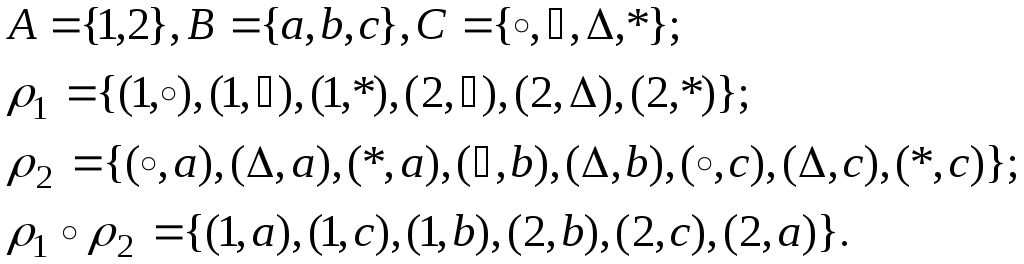
Пусть
![]() - это отношение, заданное на множестве
А, тогда бинарное отношение
- это отношение, заданное на множестве
А, тогда бинарное отношение
![]() называется
называется
-
.рефлексивным, если
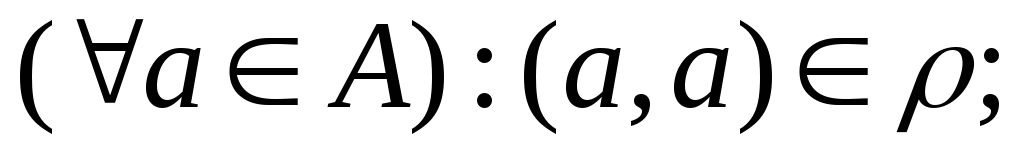
-
.антирефлексивным, если
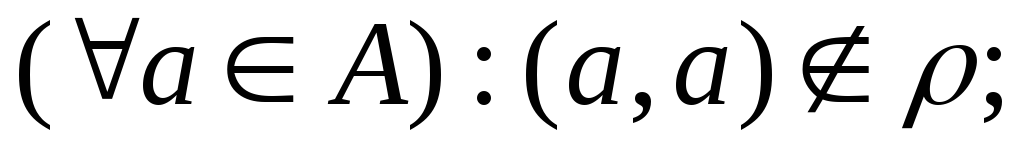
-
.симметричным, если
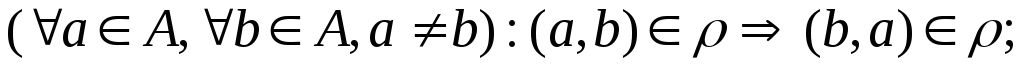
-
.антисимметричным, если
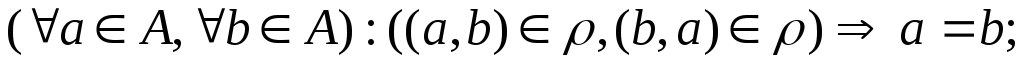
-
.транзитивным, если
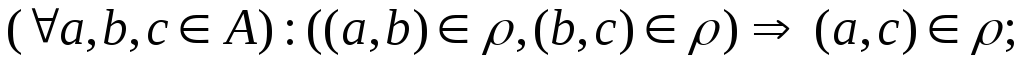
-
.полным если
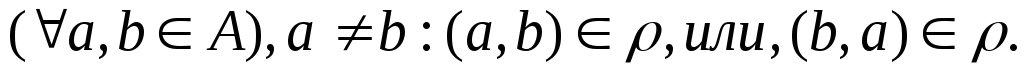
Пример 10.
Является ли
![]() рефлексивным, антирефлексивным,
симметричным, антисимметричным, полным?
рефлексивным, антирефлексивным,
симметричным, антисимметричным, полным?
![]()
1).
![]() нерефлексивно;
нерефлексивно;
например,
![]()
2).
![]() неантирефлексивно;
неантирефлексивно;
![]() ,
так как уравнение
,
так как уравнение
![]() имеет решения:
имеет решения:
![]()
3).
![]() несимметрично;
несимметрично;
например,

4).
![]() не антисимметрично.
не антисимметрично.
Пусть
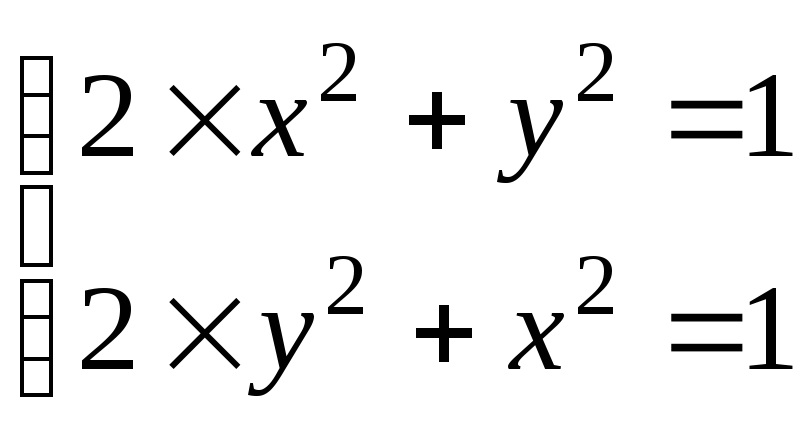
![]()
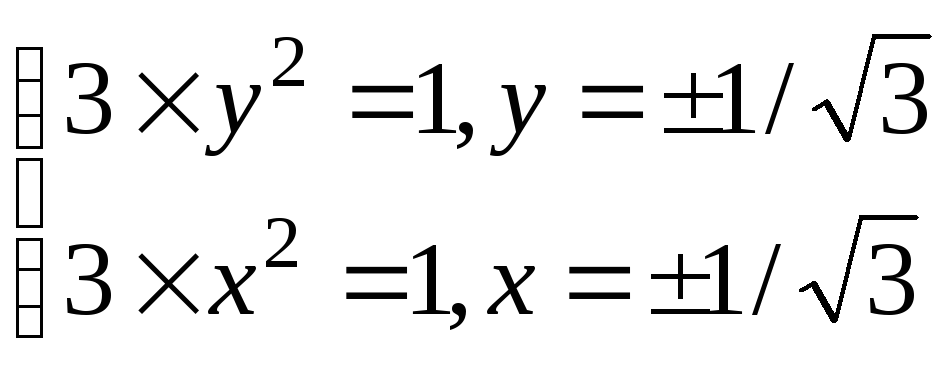 .
.
Тогда
![]()
5).
![]() не транзитивно:
не транзитивно:
например
![]()
но
![]()
6).
![]() не полное, что очевидно.
не полное, что очевидно.
Пример 11.
![]()
1).
![]() рефлексивно.
рефлексивно.
2). Пусть
![]() тогда
тогда
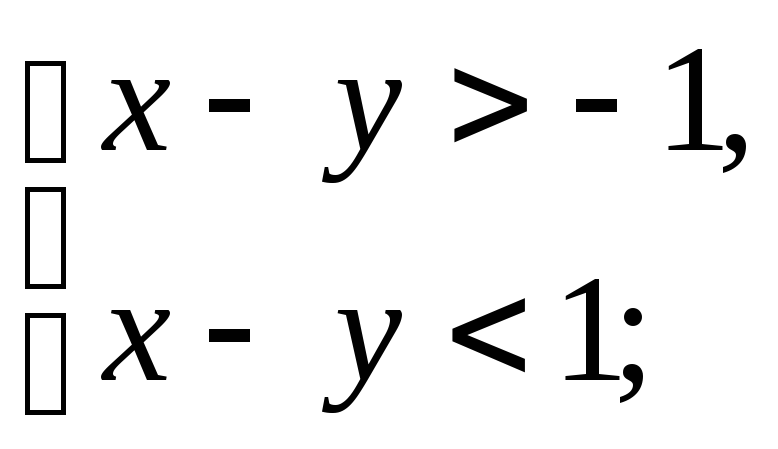
![]() т.к. х, у – целые числа
т.к. х, у – целые числа ![]() антисимметрично.
антисимметрично.
-
Пусть
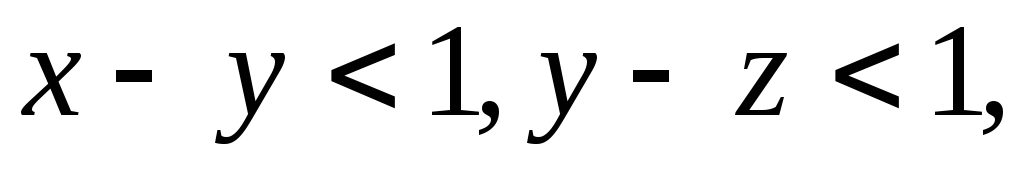 тогда
тогда
![]()
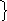
![]()
Значит
![]() транзитивно.
транзитивно.
-
Если
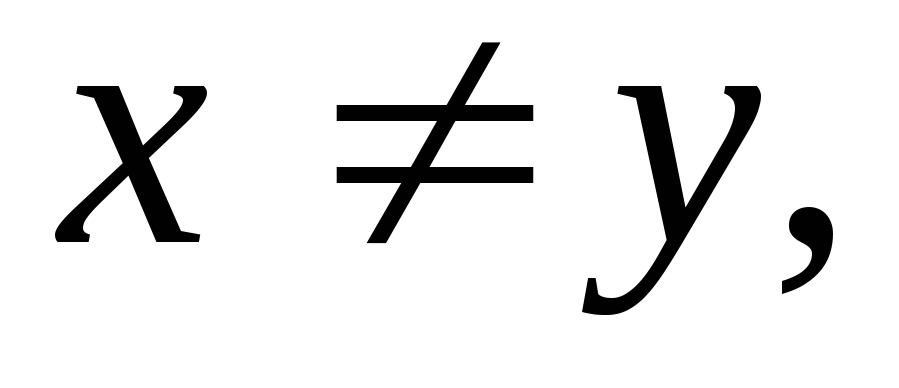 то или
то или
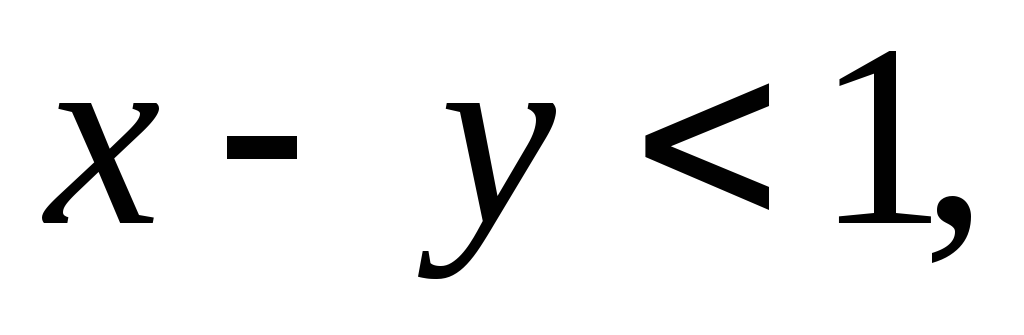 или
или
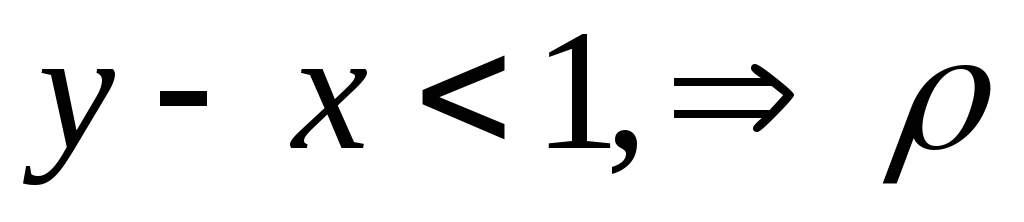 полное отношение.
полное отношение.
Теорема о свойствах бинарного отношения.
Пусть
![]() отношение на
множестве А(
отношение на
множестве А(![]() ),
тогда справедливы следующие утверждения:
),
тогда справедливы следующие утверждения:
-
 -
рефлексивно
-
рефлексивно

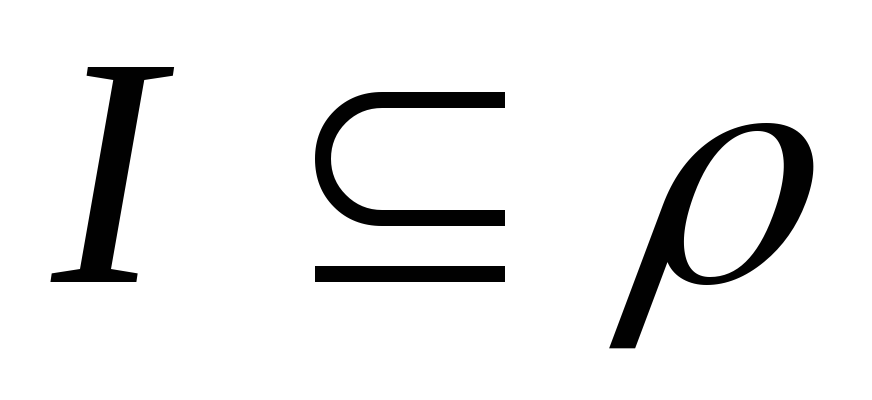 ;
; -
 симметрично
симметрично
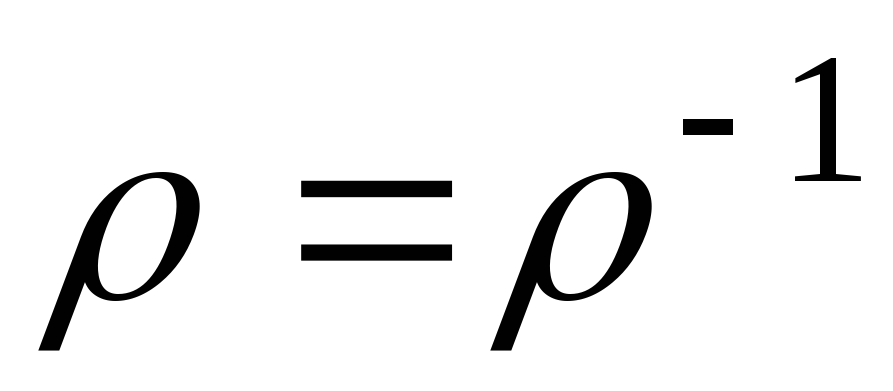 ;
; -
 транзитивно
транзитивно
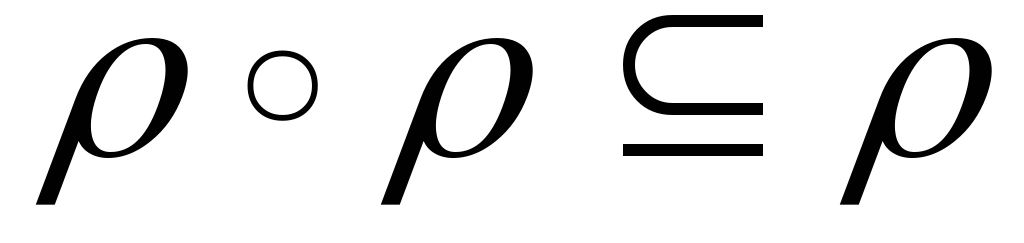 ;
; -
 антирефлексивно
антирефлексивно
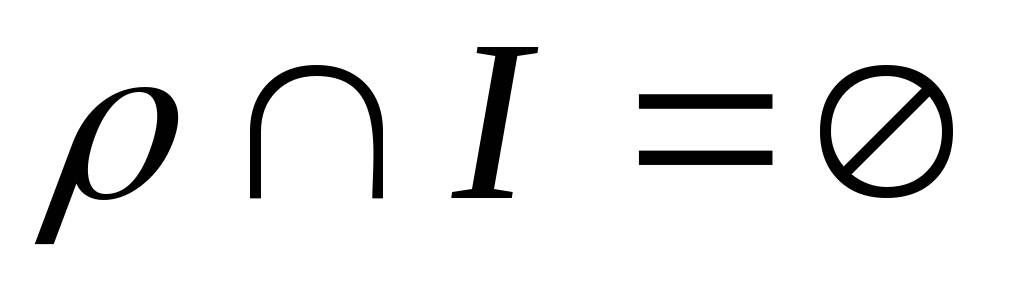 ;
; -
 антисимметрично
антисимметрично
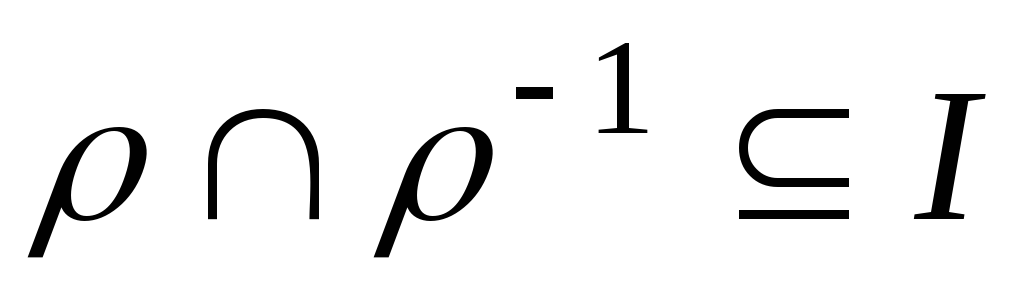 ;
; -
 полно
полно
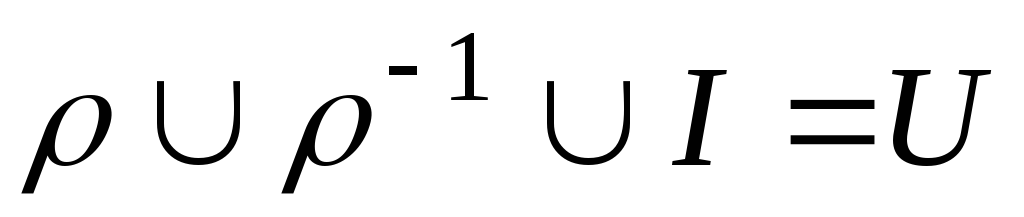 .
.
Доказательство.
1.
![]() Пусть
Пусть
![]() рефлексивно,
рефлексивно,
![]() ;
;
1.
![]() Пусть
Пусть
![]() ,
тогда
,
тогда
![]() – рефлексивно.
– рефлексивно.
2.
![]() Пусть
Пусть
![]() симметрично,
симметрично,
![]() .
.
Пусть
![]() .
.
Пусть
![]() .
Значит,
.
Значит,
![]() .
.
2.
![]() Пусть
Пусть
![]() .
Тогда
.
Тогда
![]() – симметрично.
– симметрично.
3.
![]() Пусть
Пусть
![]() транзитивно,
транзитивно,
![]() и
и
![]() Пусть
Пусть
![]() :(
:(![]() )
)![]() и (
и (![]() ;
;
3.
![]() Пусть
Пусть
![]() .
Пусть (
.
Пусть (![]() )
)![]() и
(
и
(![]()
![]() -
транзитивно.
-
транзитивно.
4.
![]() Пусть
Пусть
![]() антирефлексивно,
(
антирефлексивно,
(![]() ):
):![]() ;
;
4.
![]() Пусть
Пусть
![]() :
:
![]()
![]() антирефлексивно.
антирефлексивно.
5.
![]() Пусть
Пусть
![]() антисимметрично
(
антисимметрично
(![]() ):(
):(![]() )
)![]() и
и
![]() .
Если
.
Если
![]() и (
и (![]() )
)![]() ,
то (
,
то (![]() )
)![]() и
и
![]() ,
пересечение множеств
,
пересечение множеств
![]() и
и
![]() по парам, состоящих из разных элементов,
пусто
по парам, состоящих из разных элементов,
пусто
![]() эти множества в качестве общих могут
иметь только элементы вида
эти множества в качестве общих могут
иметь только элементы вида
![]() ,
что и означает:
,
что и означает:
![]() ;
;
5.
![]() Пусть
Пусть
![]() это означает, что в пересечение
это означает, что в пересечение
![]() могут входить только пары вида
могут входить только пары вида
![]()
![]() если
если
![]() и
и
![]() ,
то
,
то
![]() .
.
6.
![]() Пусть
Пусть
![]() -полно,
(
-полно,
(![]() ,
,
![]() ):
(
):
(![]() )
или
)
или
![]()
Но
![]()
![]()
![]() ,
,![]() обе
пары
обе
пары
![]() и
и
![]() принадлежат объединению:
принадлежат объединению:
![]()
![]()
![]() ;
;
-
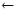 Пусть
Пусть
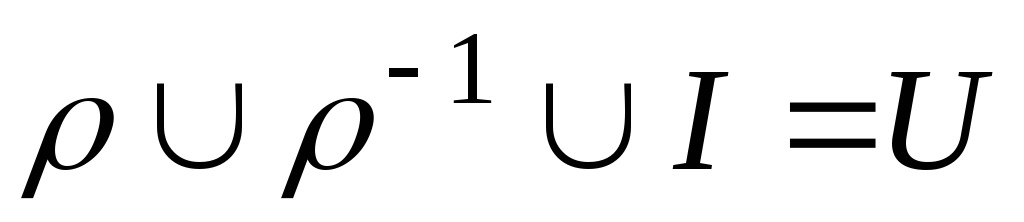 .
Если
.
Если
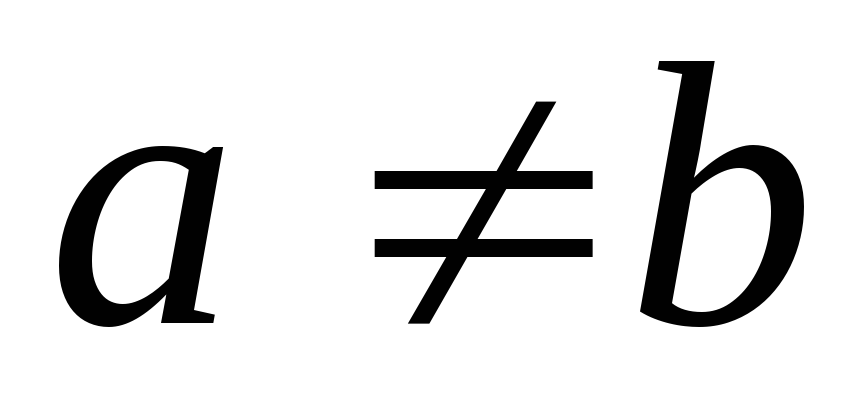 ,
то
,
то
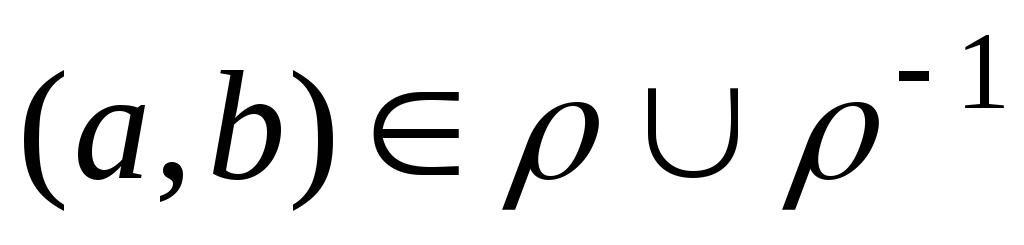 .
.
Либо
![]() .
.
Либо
![]()
![]() - полно.
- полно.
ЛЕКЦИЯ 7.
