Формула включения и исключения.

Формула включения (исключения) – это формула для нахождения числа элементов объединения нескольких конечных множеств. Выведем формулу для объединения двух множеств. Пусть Тогда (см. диаграмму Венна).

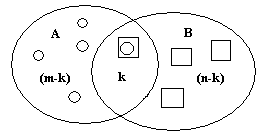
Рис. 1

Также нетрудно получить формулу для мощности объединения трех множеств:

Выведем формулу для объединения n множеств. Эта формула такова:

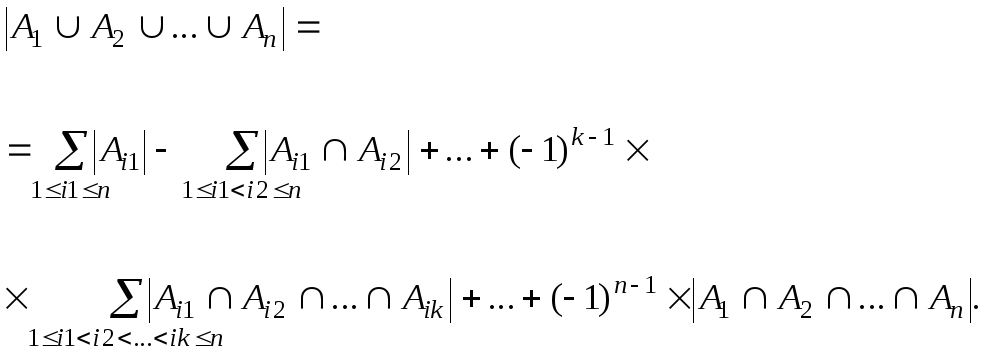(1)

Общая сумма формулы (1):

. (2)

Формула (2) – это сумма мощностей всех возможных пересечений k штук множеств, отобранных из n данных. В этой сумме слагаемых. Для доказательства формулы (1) надо доказать, что каждый элемент x из левой части формулы ровно один раз считается в правой части. Пусть x принадлежит m множествам из n имеющихся. Посчитаем, сколько раз учитывается элемент x:

- это число отдельных множеств, содержащих х;

- это число всех пересечений из двух множеств, каждое из которых содержит x;

- единственное пересечение всех m множеств, содержащих x.

Формула (1) называется формулой включения и исключения.

Пример.

Из 100 студентов английский язык знают 28 человек, немецкий – 30, французский – 42, английский и немецкий – 8, английский и французский – 10, немецкий и французский – 5, все языки знают 3 человека. Сколько человек не знают ни одного языка?

Решение.

U – это множество всех студентов,

A1 - множество студентов, знающих английский язык,

A2 - множество студентов, знающих немецкий язык,

A3 - множество студентов, знающих французский язык, тогда

Нужно найти

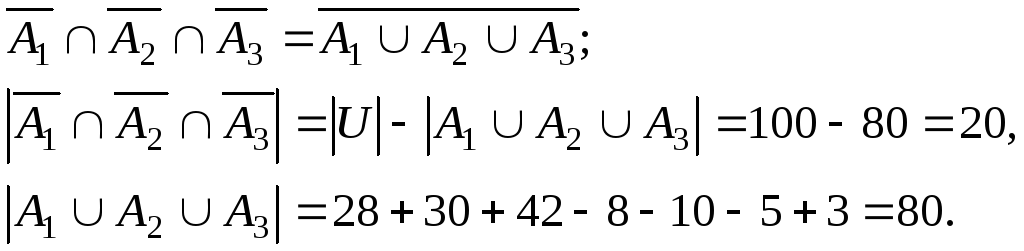так как

Лекция 6.

Термин		Перевод	Математический термин
Reflexio	лат.	Отражение	Рефлексивность
Symmetria	греч.	Гармония	Симметричность
Tranzitus	лат.	Переход	Транзитивность
Anti	греч.	Против	Анти-…
Factor	лат.	Фактор	Фактормножество
Kernel	англ.	ядро	Ядро

Таблица 2.

Упорядоченные пары.

Пусть a и b – два произвольных объекта.

Определение 1. Упорядоченной парой (a, b) называют такой набор этих объектов, в котором объект a имеет первый номер, а объект b – второй, значит если .

По аналогии с упорядоченной парой вводят понятие упорядоченного набора из n элементов, в котором каждый элемент имеет свой номер. В теории множеств упорядоченную пару (a, b) определяют как множество вида (a,b)={{a},{a,b}}.

Теорема 1.

Доказательство. Пусть {{a}, {a, b}}={{c}, {c, d}} – равные множества. Тогда они состоят из одних и тех же элементов. Возможны варианты:

1).

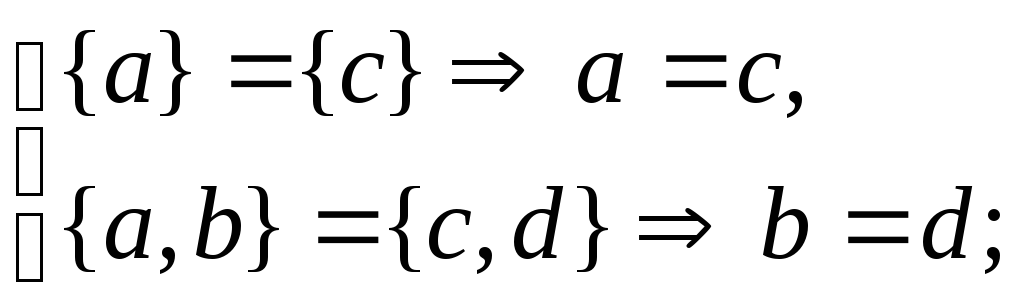
2). Т. к. одноэлементное множество не может быть равно множеству, содержащему два элемента, то если

Теорема доказана.

Прямое произведение множеств.

Пусть А и В – два множества.

Определение 2. Прямым (декартовым) произведением множеств называется множество упорядоченных пар, где первый элемент принадлежит первому множеству, а второй элемент второму.

, соответственно

Пример 1.

По аналогии с прямым произведением двух множеств вводят понятие прямого произведения n множеств как множества вида:

Обозначение:

Теорема 2.

Доказательство.

Чтобы составить упорядоченную пару, надо выполнить два действия:

1. выбрать первый элемент пары;

2. выбрать второй элемент пары.

Первое действие можно выполнить m способами, если элемент выбирать из множества А и n способами, если элемент выбирать из множества В. Второе действие можно выполнить n способами, если элемент выбирается из множества В и m способами, - если из множества А. По принципу умножения

Теорема доказана.