Лекция 5. Свойства операций над множествами.

Термин		Перевод	Математический термин
Idem	лат.	то же самое, тот же, равным образом	идемпотентность
Commutare	лат.	менять, перемещать	коммутативность
Associare	лат.	присоединять	ассоциативность
Distribution	англ.	распределять	дистрибутивность
Involutio	лат.	свертывание, возвращение назад	инволютивность
Conjunctio	лат.	соединение, связь	конъюнкция
Disjunctivus	лат.	разделение	дизъюнкция
Infixus	лат.	вставленный	инфикс (инфиксный)
Praefixum	лат.	прикрепленный впереди	префикс
Binaurus	лат.	двойной	бинарный

Таблица 1.

Переводы терминов.

Пусть, Каковы бы ни были заданные произвольные подмножества универсума U, для них справедливы соотношения:

1. Идемпотентность.

2. Коммутативность.

3. Ассоциативность.

4. Дистрибутивность.

5. Законы поглощения.

6. Свойства нуля.

7. Свойства единиц.

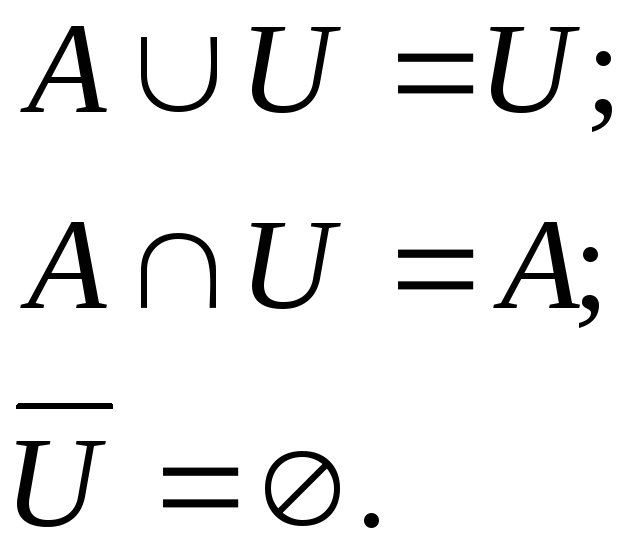
8. Инволютивность.

9. Законы де Моргана.

10. Свойства дополнения.

В качестве примера доказательств приведем доказательства одного из законов дистрибутивности и одного из законов де Моргана.

Теорема 1. .

Доказательство.

• Пусть

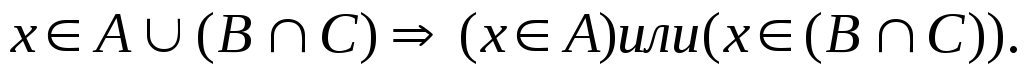
а) Пусть

б) Пусть

Вывод:

• Пусть .

а) Пусть

б) Пусть

Вывод. .

Окончательно .

Теорема доказана.

Теорема 2. .

Доказательство.

1. Пусть

2. Пусть

Из 1. и 2. следует, что равны.

Законы коммутативности и ассоциативности легко распространяются на случай объединения (пересечения) любого конечного числа множеств. Именно, в какой бы последовательности не объединялись (пересекались) данные множества , в результате получится одно и тоже множество, которое обозначается ; объединение состоит из тех и только тех элементов, которые входят хотя бы в одно из данных множеств (пересечение содержит те и только те элементы, которые входят во все множества одновременно).

Запишем обобщение законов дистрибутивности и де Моргана:

Доказательство проводится, например, методом математической индукции.

Теорема 3. Пусть

Тогда справедливы следующие утверждения:

Если для всякого множества выполняется , то

Если для всякого множества выполняется , то

Если выполняется , то

Доказательство.

1. Пусть

Положим

2. Пусть

Возьмем

3. Пусть

а)

б)

Теорема 4. Следующие четыре утверждения попарно эквивалентны:

1. 

2. 

3. 

4. 

Чтобы доказать все двенадцать теорем, достаточно доказать замкнутую цепочку теорем. Справедливость теорем удобно проверить, используя диаграмму Венна.

Для примера докажем замкнутую цепочку теорем вида 4.1. 2. 3. 4. Т. е., докажем, что

Доказательство.

1. Дано:

Доказать. .

Доказательство.

Пусть

2. Дано: .

Доказать. .

Доказательство.

1.

2.Пусть

3.

2. Дано: .

Доказать. .

Доказательство.

1.

2. Пусть

3.

2. Дано: .

Доказать.

Доказательство.

Пусть

Теорема доказана.