Лекция 4. Операции над множествами. Сравнение множеств.
Определение 1. Говорят, что
множество A
содержится во множестве B
(обозначение
)
(А подмножество B,
А включено в B, В
содержит/ включает A,
A и B
состоят в отношении включения, всякий
элемент множества A
принадлежит и множеству В), если
Определение 2. Говорят, что
множество A
есть собственное подмножество множества
B (обозначение
A
В)
(В строго включает А), если
и В
А:
Следовательно, если неверно, что
,
обозначение:
,
то можно записать, что
.
Свойства отношения включения.
10.
для всякого множества A;
20. Если
и
,
то
– транзитивность. Доказательство
элементарно.
Определение 3. Мощностью
конечного множества называют число
элементов, входящих в это множество.
Обозначается:
.
Теорема 1. Если A
– произвольное множество, то
.
Доказательство. Допустим, что
утверждение неверно и
.
Тогда должно выполняться условие:
.
Но это противоречие, т. к. пустое множество
ничего не содержит.
Теорема доказана.
Определение 4. Булеаном
множества А (обозначение 2А)
называется множество всех подмножеств
данного множества А: 2А={B|B
A}.
Если
то
.
Пример 1.
Теорема 2.
.
Доказательство (1 способ). Пронумеруем элементы множества А: А = {a1, a2, …, an} и закодируем всякое подмножество В множества А последовательностью длины n, состоящей из нулей и единиц:
Пустое множество кодируется n нулями,
а множество А – n единицами.
Каждому подмножеству В ставится в
соответствие своя последовательность,
и, наоборот, по каждой последовательности
единственным образом восстанавливается
подмножество В. Число всех подмножеств
множества А равно числу последовательной
длины n, состоящих из
нулей и единиц. По принципу умножения
имеем:
Теорема доказана.
Доказательство (2 способ). Число
подмножеств мощности k
равно числу способов отобрать из n
элементов множества А k
элементов, образующих данное подмножество,
т.е. равно числу
.
Следовательно,
Теорема доказана.
Операции над множествами.
Определение 1. Объединением
или суммой (обозначение
или +) двух множеств А и В называется
множество, состоящее из тех и только
тех элементов, которые принадлежат хотя
бы одному из этих двух множеств:
В устной речи операцию объединения описывают союзом “или”.
Пример 1.
Определение 2. Пересечением
(обозначение
или
или АВ) двух множеств А и В
называется множество, состоящее из тех
и только тех элементов, которые принадлежат
обоим множествам:
В устной речи операции пересечения соответствует союз “и”.
Пример 2.
Определение 3. Два множества
называются непересекающимися,
если АВ=
и пересекающимися, если АВ
Пример 3.
Определение 4. Пусть
семейство множеств
Ei,
каждое из которых включено во множество
А. Семейство
называется покрытием множества
А, если всякий элемент множества А
входит, по крайней мере, в одно множество
семейства .
Пример 4.
Определение 5. Семейство называется разбиением множества А, если всякий элемент множества А принадлежит ровно одному множеству семейства .
Пример 5.
Определение 6. Разностью
множеств А и В
(обозначение
)
называется множество, которое содержит
те и только те элементы, которые
принадлежат множеству А и не
принадлежат множеству В:
Пусть
т. к. во множестве А нет ни одного
элемента, который не ходил бы в множество
В. И наоборот:
,
т. к. каждый элемент из множества А
принадлежит множеству В.
Пример 6.
Определение 7. Симметрической
разностью множеств А и
В (обозначение А
В)
называется множество, состоящее из тех
и только тех элементов, которые принадлежат
ровно одному из множеств:
Пример 7.
Определение 8. Операция
дополнения множества А (обозначение
)
вводится, когда задан универсум U.
Дополнением множества А
до универсума U
называют множество, состоящее из тех и
только тех элементов, которые не
принадлежат А:
Пример 8.
Теорема.
Доказательство.
-
Пусть
-
Пусть
из 1) и 2) следует, что
Теорема доказана.
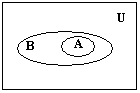
Диаграммы Венна.
На диаграммах Венна универсум изображается прямоугольником или квадратом, а множества – областями внутри универсума. С помощью диаграммы Венна операции над множествами становятся наглядными.
1).
5).
2).
3).
4).
6).
7).
8).
